Dấu của tam thức bậc 2 – Lý thuyết và bài tập SGK có đáp án chi tiết nhất
Dấu của tam thức bậc 2 là một trong những nội dung tuy cơ bản nhưng có vai trò quan trọng trong việc giải quyết các bài toán THPT nói chung và Toán 10 nói riêng. Ta thường bắt gặp kiến thức này trong các bài kiểm tra cuối kì cũng như trong các kì thi quan trọng như THPT. Biết được điều đó, hôm nay HocThatGioi sẽ gửi đến các bạn bài viết Dấu của tam thức bậc 2 – Lý thuyết và bài tập SGK có đáp án chi tiết nhất để bạn đọc có thể nắm vững kiến thức này nhé!
I. Lý thuyết dấu của tam thức bậc 2
1. Tam thức bậc hai (một ẩn)
Tam thức bậc hai (đối với x) là biểu thức dạng ax^2+bx+c. Trong đó a, b, c là những số cho trước với a \neq 0
Nghiệm của phương trình ax^2+bx+c được gọi là nghiệm của tam thức bậc hai f(x)=ax^2+bx+c; \Delta =b^2−4ac và \Delta ′=b′^2−ac theo thứ tự được gọi là biệt thức và biệt thức thu gọn của tam thức bậc hai f(x)=ax^2+bx+c
2. Dấu của tam thức bậc hai
Người ta đã chứng minh được định lí về dấu tam thức bậc hai sau đây:
Định lí
Cho tam thức bậc hai f(x)=ax^2+bx+c (a\neq 0) có biệt thức \Delta=b^2–4ac
- Nếu \Delta<0 thì f(x) luôn cùng dấu với hệ số aa với mọi x \in R
- Nếu \Delta=0 thì f(x) có nghiệm kép x=\frac{-b}{2a}
- Khi đó f(x) có cùng dấu với hệ số aa với mọi x \neq \frac{-b}{2a}
- Nếu \Delta >0,f(x) có 2 nghiệm x1,x2(x1<x2) và luôn cùng dấu với hệ số a với mọi x \in (− \infty ;x_1)∪(x_2;+ \infty ) và luôn trái dấu với hệ số a với mọi x \in (x_1;x_2)
Định lí về dấu của tam thức bậc hai có minh họa hình học sau:
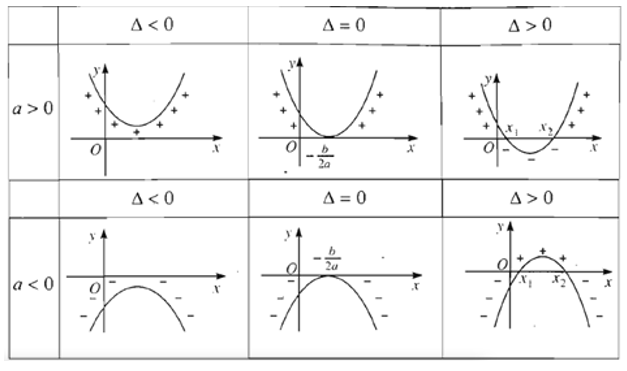
Nhận xét: Cho tam thức bậc hai ax^2+bx+c:
- ax^2+bx+c>0, \forall x \in R \Longleftrightarrow \left\{\begin{matrix} & a>0\\ & \Delta<0 \end{matrix}\right.
- ax^2+bx+c>=0, \forall x \in R \Longleftrightarrow \left\{\begin{matrix} & a>0\\ & \Delta<=0 \end{matrix}\right.
- ax^2+bx+c<0, \forall x \in R \Longleftrightarrow \left\{\begin{matrix} & a<0\\ & \Delta<0 \end{matrix}\right.
- ax^2+bx+c<=0, \forall x \in R \Longleftrightarrow \left\{\begin{matrix} & a<0\\ & \Delta<=0 \end{matrix}\right.
=> Xem thêm Dấu của nhị thức bậc nhất – Lý thuyết và bài tập SGK có đáp án chi tiết nhất
II. Giải bài tập SGK dấu của tam thức bậc 2
Bài 1 trang 105
a) 5x^2−3x+1
b) −2x^2+3x+5
c) x^2+12x+36
d) (2x−3)(x+5)

Bài 2 trang 105
a) f(x)=(3x^2−10x+3)(4x−5)
b) f(x)=(3x^2−4x)(2x^2−x−1)
c) f(x)=(4x^2−1)(−8x^2+x−3)(2x+9)
d) f(x)=\frac{(3x^2−x)(3−x^2)}{4x^2+x−3}

Bài 3 trang 105
a) 4x^2−x+1<0
b) −3x^2+x+4≥0
c) \frac{1}{x^2−4}<\frac{3}{3x^2+x−4}
d) x^2−x−6≤0
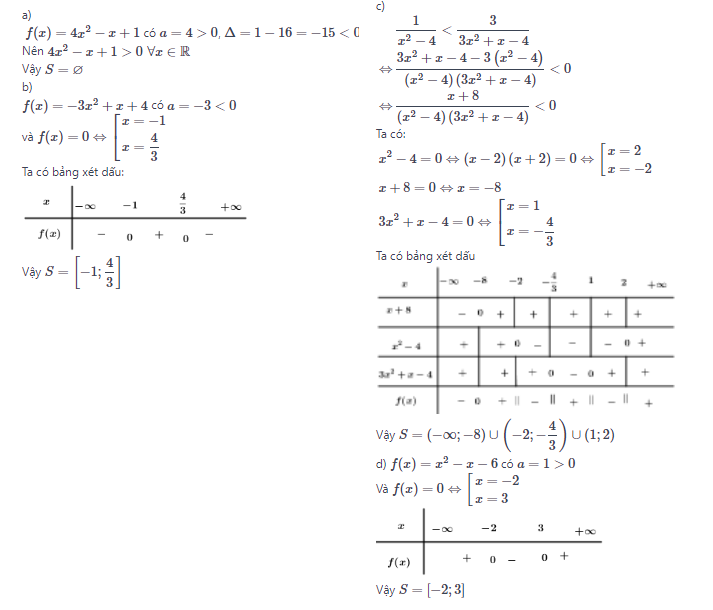
Bài 4 trang 105
a) (m−2)x^2+2(2m−3)x+5m−6=0
b) (3−m)x^2−2(m+3)+m+2=0
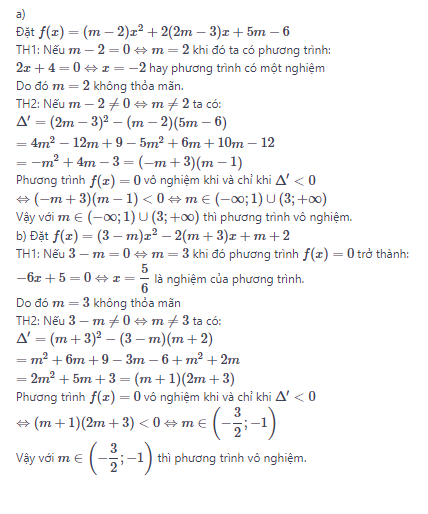
Trên đây là toàn bộ bài viết của HocThatGioi về Dấu của tam thức bậc 2 – Lý thuyết và bài tập SGK có đáp án chi tiết nhất. Nếu thấy bài viết bổ ích, hãy chia sẽ bài viết này cho bạn bè để cùng nhau học thật giỏi nhé! Chúc các bạn học tốt!





