Giải SGK bài 19 Phương trình đường thẳng Toán 10 Kết nối tri thức Tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Phương trình đường thẳng. Đây là bài học thuộc bài 19 chương VII trang 30, 31, 32, 33, 34, 35 sách Toán 10 Kết nối tri thức tập 2. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi trong SGK của bài 19
Dưới đây là phương pháp và bài giải chi tiết cho câu hỏi hoạt động cùng phần luyện tập ở các trang 31, 32, 33, 34 trong bài Phương trình đường thẳng. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động 1 trang 31
Tập hợp tất cả những điếm $\mathrm{M}$ để $\overrightarrow{A M}$ vuông góc với $\vec{n}$ là đường thẳng qua $\mathrm{A}$ và vuông góc với giá của vectơ $\vec{n}$.
Hoạt động 2 trang 31
$$a\left(x-x_o\right)+b\left(y-y_o\right)=0 .$$
Gọi $M(x ; y)$
Ta có: $\overrightarrow{A M}=\left(x-x_o ; y-y_o\right), \vec{n}=(a ; b)$
$M \in \Delta \Leftrightarrow \overrightarrow{A M} \perp \vec{n}$
Hay $\overrightarrow{A M} \cdot \vec{n}=0 \Leftrightarrow a\left(x-x_o\right)+b\left(y-y_o\right)=0(ĐPCM)$
Luyện tập 1 trang 32
$\overrightarrow{B C}$ là vevtơ pháp tuyến của đường thẳng $\mathrm{AH}$.
Đường cao $\mathrm{AH}$ đi qua điếm $A(-1 ; 5)$ có một vectơ pháp tuyến là $\overrightarrow{n_{A H}}=\overrightarrow{B C}=(4 ;-2)$.
Phương trình tổng quát của AH là: $4(x+1)-2(y-5)=0 \Leftrightarrow 2 x-y+7=0$.
Luyện tập 2 trang 32
Ta có $\Delta: y=3 x+4 \Leftrightarrow \Delta: 3 x-y+4=0$
Vậy vectơ pháp tuyến của $\Delta$ là $\vec{n}=(3 ;-1)$.
Hoạt động 3 trang 32
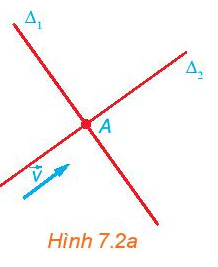
Quan sát Hình 7.2a ta thấy giá của vectơ song song với đường thẳng $\Delta_2$ nên vật thể chuyển động với vận tốc bằng $\vec{v}$ và đi qua A thì nó di chuyển trên đường $\Delta_2$.
Luyện tập 3 trang 33
Tìm vectơ pháp tuyến, từ đó suy ra vectơ chỉ phương của đường thẳng.
Ta có: $\overrightarrow{n_{\Delta}}=(2 ;-1)$, suy ra $\overrightarrow{u_{\Delta}}=(1 ; 2)$
Hoạt động 4 trang 33
a) Hỏi vật thể chuyển động trên đường thẳng nào (chỉ ra điểm đi qua và vectơ chỉ phương của đường thẳng đó)?
b) Chứng minh rằng, tại thời điểm $t(t>0)$ tính từ khi khởi hành, vật thể ở vị trí có toạ độ là $(2+3 t ; 1+4 t)$
a) Vật thể đi qua điểm $A(2 ; 1)$ và đi theo hướng vectơ $\vec{v}(3 ; 4)$.
b) Sau thời gian $t$ thì vectơ vận tốc của vật thế là: $t \vec{v}=(3 t ; 4 t)$.
Vậy tọa độ của vật thể sau thời gian t là: $\overrightarrow{O A}+t \vec{v}=(2+3 t ; 1+4 t)$.
Luyện tập 4 trang 33
Hai đường thẳng song song thì hai vectơ pháp tuyến cùng phương.
Vì hai đường thẳng $\Delta$ và d song song với nhau nên ta có thể chọn $\overrightarrow{n_{\Delta}}=\overrightarrow{n_d}=(3 ;-4)$.
Mặt khác, $\Delta$ đi qua điểm $M(-1 ; 2)$ nên phương trình $\Delta$ là:
$$3(x+1)-4(y-2)=0 \Leftrightarrow 3 x-4 y+11=0 .$$
Luyện tập 5 trang 33
$\overrightarrow{A B}$ là vevtơ chỉ phương của đường thẳng $A B$.
Đường thẳng $A B$ đi qua điểm $A\left(x_1 ; y_1\right)$ có vectơ chỉ phương là $\overrightarrow{u_{A B}}=\overrightarrow{A B}=\left(x_2-x_1 ; y_2-y_1\right)$
Do đó, AB có phương trình tham số là:
$\left\{\begin{array}{l}x=x_1+\left(x_2-x_1\right) t \\ y=y_1+\left(y_2-y_1\right) t\end{array}\right.$
Chọn $\overrightarrow{n_{A B}}=\left(y_2-y_1 ;-\left(x_2-x_1\right)\right)$, suy ra $\mathrm{AB}$ có phương trình tổng quát là:
$$\left(y_2-y_1\right)\left(x-x_1\right)-\left(x_2-x_1\right)\left(y-y_1\right)=0$$
Vận dụng trang 34
– Nước đóng băng ở $0^{\circ} \mathrm{C}, 32^{\circ} \mathrm{F}$.
– Nước sôi ở $100^{\circ} \mathrm{C}, 212^{\circ} \mathrm{F}$.
Trong quy đổi đó, nếu $a^{\circ} \mathrm{C}$ tương ứng với $b^{\circ} \mathrm{F}$ thì trên mặt phẳng toạ độ $\mathrm{Oxy}$, điểm $M(a ; b)$ thuộc đường thẳng đi qua $A(0 ; 32)$ và $B(100 ; 212)$. Hỏi $0^{\circ} \mathrm{F}, 100^{\circ} \mathrm{F}$ tương ứng với bao nhiêu?
Viết phương trình đường thẳng $\mathrm{AB}$, từ đó tìm được mối liên hệ giữa hoành độ (độ $\mathrm{C}$ ) với tung độ (độ $\mathrm{F}$ ).
Ta có $\overrightarrow{u_{A B}}=\overrightarrow{A B}=(100 ; 180)$ suy ra $\overrightarrow{n_{A B}}=\left(9_1 ;-5\right)$.
Mặt khác $A B$ đi qua điếm $A(0 ; 32)$ nên phương trình của $A B$ là $9 x-5 y+160=0 \Leftrightarrow x=\frac{5 y-160}{9}$.
Với $y=0^{\circ} F$ ta có: $x=\frac{5.0-160}{9}=\left(\frac{-160}{9}\right)^{\circ} C$
Với $y=100^{\circ} F$ ta có: $x=\frac{5.100-160}{9}=\left(\frac{340}{9}\right){ }^{\circ} C$
Vậy $0^{\circ} F, 100^{\circ} F$ tương ứng xấp xỉ $-18^{\circ} \mathrm{C}, 38^{\circ} \mathrm{C}$.
Giải bài tập vận dụng trang 34 SGK Toán 10 bài 19
Phần tiếp theo sẽ cung cấp cho các bạn phương pháp cùng lời giải trong phần bài tập trang 34, 35 cực kỳ dễ hiểu và chi tiết. Cùng HocThatGioi rèn luyện và nâng cao kỹ năng giải quyết các vấn đề thực tế thông qua các phương pháp, công thức toán học từ bài Phương trình đường thẳng ở trên.
Bài tập 7.1 trang 34
a) Lập phương trình tổng quát của đường thẳng $\Delta_1$ đi qua $A$ và có vectơ pháp tuyến $\vec{n}$.
b) Lập phương trình tham số của đường thẳng $\Delta_2$, đi qua $\mathrm{B}$ và có vectơ chỉ phương $\vec{v}$.
c) Lập phương trình tham số của đường thẳng $\mathrm{AB}$.
Phương trình tổng quát của đường thẳng $\Delta$ đi qua điểm $M_o\left(x_o ; y_o\right)$ và nhận $\vec{n}=(\mathrm{a} ; \mathrm{b})(\vec{n} \neq 0)$ làm vectơ pháp tuyến là: $a\left(x-x_o\right)+b\left(y-y_o\right)=0$.
Phương trình tham số của đường thẳng $\Delta$ đi qua điểm $M_o\left(x_o ; y_o\right)$ và nhận $\vec{u}=(\mathrm{a} ; \mathrm{b})(\vec{u} \neq 0)$ làm vectơ chỉ phương là: $\left\{\begin{array}{l}x=x_o+a t \\ y=y_o+b t\end{array}\right.$ ( $t$ là tham số )
a) Phương trình tổng quát của đường thẳng $\Delta_1$ là̀:
$2(x-1)+1(y-3)=0 \Leftrightarrow 2 x+y-5=0$.
b) Phương trình tham số của đường thẳng $\Delta_2$ là: $\left\{\begin{array}{l}x=-2+3 t \\ y=1+2 t\end{array}\right.$
c) Phương trình đường thẳng $\mathrm{AB}$ đi qua điểm $A(1 ; 3)$ nhận $\overrightarrow{A B}=(-3 ;-2)$ là vectơ chỉ phương nên phương trình tham số của $\mathrm{AB}$ là $\left\{\begin{array}{l}x=1-3 t \\ y=3-2 t\end{array}\right.$
Bài tập 7.2 trang 34
Trục số $O x, O y$ đi qua điểm $O$ và có vectơ pháp tuyến lần lượt là $\vec{j}=(0 ; 1) ; \vec{i}=(1 ; 0)$.
Trục $\mathrm{O} y$ đi qua $O(0 ; 0)$ và nhận $\vec{i}=(1 ; 0)$ là vectơ pháp tuyến, do đó phương trình tổng quát của trục $\mathrm{Ox}$ là $1 .(x-0)+0 .(y-0)=0 \Leftrightarrow x=0$.
Trục $\mathrm{O} x$ đi qua $O(0 ; 0)$ và nhận $\vec{j}=(0 ; 1)$ là vectơ pháp tuyến, do đó phương trình tổng quát của trục Oy là $0 .(x-0)+1 .(y-0)=0 \Leftrightarrow y=0$.
Bài tập 7.3 trang 34
a) Lập phương trình tổng quát của $\Delta_1$
b) Lập phương trình tham số của $\Delta_2$
Phương trình tổng quát của đường thẳng $\Delta$ đi qua điểm $M_o\left(x_o ; y_o\right)$ và nhận $\vec{n}=(\mathrm{a} ; \mathrm{b})(\vec{n} \neq 0)$ làm vectơ pháp tuyến là: $a\left(x-x_o\right)+b\left(y-y_o\right)=0$.
Phương trình tham số của đường thẳng $\Delta$ đỉ qua điếm $M_o\left(x_o ; y_o\right)$ và nhận $\vec{u}=(\mathrm{a} ; \mathrm{b})(\vec{u} \neq 0)$ làm vectơ chỉ phương là: $\left\{\begin{array}{l}x=x_o+a t \\ y=y_o+b t\end{array}\right.$ (t là tham số )
a) Đường thẳng $\Delta_1$ có một vectơ chỉ phương là $\vec{u}_{\Delta_1}=(2 ; 5)$
Do đó $\vec{n}_{\Delta_1}=(-5 ; 2)$, đồng thời $\Delta_1$ đi qua điểm $M(1 ; 3)$ nên phương trình tống quát của $\Delta_1$ là: $-5(x-1)+2(y-3)=0 \Leftrightarrow 5 x-2 y+1=0$.
b) Đường thẳng $\Delta_2$ có một vectơ pháp tuyến là $\vec{n}_{\Delta_2}=(2 ; 3)$
Do đó $\vec{u}_{\Delta_1}=(-3 ; 2)$, đồng thời $\Delta_2$ đi qua điểm $N(1 ; 1)$ nên phương trình tham số của $\Delta_2$ là: $\left\{\begin{array}{l}x=1-3 t \\ y=1+2 t\end{array}\right.$.
Bài tập 7.4 trang 34
a) Lập phương trình đường cao kẻ từ $A$.
b) Lập phương trình đường trung tuyến kẻ từ $\mathrm{B}$.
a) Đường cao kẻ từ $\mathrm{A}$ đi qua $\mathrm{A}$ có vectơ pháp tuyến là $\overrightarrow{B C}$.
b) Đường trung tuyến kẻ từ $\mathrm{B}$ đi qua hai điểm $\mathrm{B}$ và $\mathrm{M}$ trong $\mathrm{M}$ là trung điểm của cạnh $\mathrm{AC}$.
a) Đường cao kẻ từ $\mathrm{A}$ của tam giác $\mathrm{ABC}$ là đường thẳng đi qua $\mathrm{A}$ và có vectơ pháp tuyến là $\overrightarrow{B C}=(-5 ;-1)$ nên phương trình đường cao đó là:
$-5(x-1)-1(y-2)=0 $
$\Leftrightarrow-5 x-y+7=0$
Hay $5 x+y-7=0$
b) Gọi M là trung điểm AC. Khi đó:
\begin{cases} x_M= \frac{\mathrm{x_A+x_C} }{\mathrm{2}} = \frac{\mathrm{1+(-2)} }{\mathrm{2} }= -\frac{\mathrm{1} }{\mathrm{2}}\\ y_M= \frac{\mathrm{y_A+y_C} }{\mathrm{2}} = \frac{\mathrm{2+(-1)} }{\mathrm{2} }= \frac{\mathrm{1} }{\mathrm{2}} \\ \end{cases} \\\\ \Rightarrow M( -\frac{\mathrm{1} }{\mathrm{2} } ; \frac{\mathrm{1} }{\mathrm{2}})
Trung tuyến BM đi qua điểm $B(3 ; 0)$ nhận vectơ $\overrightarrow{u_{B M}}=2 \overrightarrow{B M}=(-7 ; 1)$ là vectơ chỉ phương nên phương trình tham số của BM là $\left\{\begin{array}{l}x=3-7 t \\ y=t\end{array}\right.$.
Bài tập 7.5 trang 34
Chứng minh rằng, đường thẳng đi qua hai điểm $A(a ; 0), B(0 ; b)$ với $a b \neq 0(H .7 .3)$ có phương trình là: $$\frac{x}{a}+\frac{y}{b}=1$$
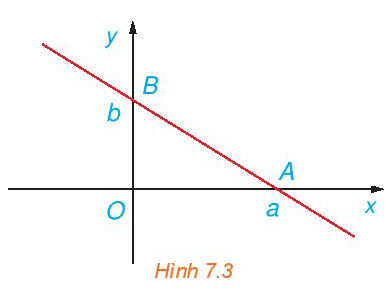
Viết phương trình tổng quát của $\mathrm{AB}$ rồi biến đổi phương trình về dạng cần chứng minh.
Đường thẳng $\mathrm{AB}$ có một vectơ chỉ phương là $\overrightarrow{u_{A B}}=\overrightarrow{A B}=(-a ; b)$.
Do đó: $\overrightarrow{n_{A B}}=(b ; a)$
Phương trình tổng quát của đường thẳng $\mathrm{AB}$ có vectơ pháp tuyến $\overrightarrow{n_{A B}}=(b ; a)$ và đi qua điểm $A(a ; 0)$ là:
b(x-a)+a(y-0) \\\\ \Leftrightarrow b x+a y-a b=0 \\\\ \Leftrightarrow \frac{x}{a}+\frac{y}{b}=1 .
Bài tập 7.6 trang 34, 35
$$\left\{\begin{array}{l}x=21,2-\frac{153}{40} t \\y=105,8+\frac{9}{5} t\end{array}\right.$$
a) Hỏi chuyến bay từ Hà Nội đến Đà Nẵng mất mấy giờ?
b) Tại thời điểm 1 giờ kể từ lúc cất cánh, máy bay đã bay qua vĩ tuyến 17 (17° Bắc) chưa?
a) Thời gian bay từ Hà Nội đến Đà Nẵng ứng với tham số t thỏa mãn tọa độ của sân bay Đà Nẵng.
b) Tìm hoành độ tại thời điểm $t=1$, rồi rút ra kết luận.
a) Máy bay đến sân bay Đà Nẵng ứng với thời gian t (giờ) thỏa mãn:
\begin{cases} 16,1=21,2 – \frac{\mathrm{153} }{\mathrm{40}} t \\ 108,2=105,8 +\frac{\mathrm{9} }{\mathrm{5}} t \\ \end{cases} \\\\ \Longleftrightarrow \begin{cases} \frac{\mathrm{153} }{\mathrm{40}} t=5,1 \\ \frac{\mathrm{9} }{\mathrm{5}} t=2,4 \\ \end{cases} \\\\ \Longleftrightarrow \begin{cases} t= \frac{\mathrm{4} }{\mathrm{3}} \\ t= \frac{\mathrm{4} }{\mathrm{3}} \\\end{cases} \\\\ \Longleftrightarrow t= \frac{\mathrm{4} }{\mathrm{3}}
Chuyến bay từ Hà Nội đến Đà Nẵng mất $\frac{4}{3}$ giờ.
b) Tại thời điếm $t=1$ giờ, ta có $x=21,2-\frac{153}{40} .1=17,375$
Vậy tại thời điếm 1 giờ sau khi cất cánh, máy bay ở vị trí có vĩ độ $17,375^{\circ}$ Bắc nên máy bay đã bay qua vĩ tuyến 17
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Phương trình đường thẳng Chương phương pháp tọa độ trong mặt phẳng Toán 10 Kết nối tri thức tập 2 ở các trang 30, 31, 32, 33, 34, 35. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!





