Hệ thức lượng trong tam giác và giải tam giác – Lý thuyết và bài tập có đáp án
Các hệ thức lượng trong tam giác hay giải tam giác là một những kiến thức cơ bản nhưng quan trọng bậc nhất trong chương trình Toán THPT nói chung và Toán 10 nói riêng. Biết được điều đó, hôm nay HocThatGioi sẽ gửi đến các bạn bài viết Hệ thức lượng trong tam giác và giải tam giác – Lý thuyết và bài tập có đáp án để bạn đọc có thể nắm vững nội dung này nhé! Khám phá ngay thôi!

I. Lý thuyết hệ thức lượng trong tam giác và giải tam giác
1. Nhắc lại hệ thức lượng trong tam giác vuông
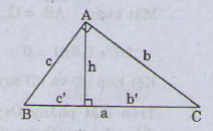
Cho tam giác ABC vuông góc tại đỉnh A (góc A bằng 90 độ), ta có:
- b^2=ab′;c^2=a.c′
- Định lý Pitago : a^2=b^2+c^2
- a.h=b.c
- h^2=b′.c′
- \frac{1}{h^2}=\frac{1}{b^2}+\frac{1}{c^2}
2. Định lý cosin
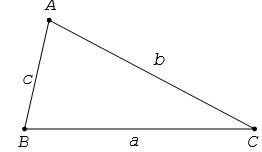
Định lí: Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng
Cho tam giác ABC có BC = a, AC = b và AB = c, ta có các hệ thức sau:
- a^2=b^2+c^2−2bc.cosA(1)
- b^2=a^2+c^2−2ac.cosB(2)
- c^2=a^2+b^2−2ab.cosC(3)
Hệ quả:
- cos A=\frac{b^2+c^2-a^2}{2bc}
- cos B=\frac{a^2+c^2-b^2}{2ac}
- cos C=\frac{a^2+b^2-c^2}{2ab}
Áp dụng: Tính độ dài đường trung tuyến của tam giác
Cho tam giác ABC có các cạnh BC=a, CA=b và AB=c. Gọi m_a,m_b và m_c là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A,B,C của tam giác. Ta có
- m_a^2=\frac{2(b^2+c^2)-a^2}{4}
- m_b^2=\frac{2(a^2+c^2)-b^2}{4}
- m_c^2=\frac{2(a^2+b^2)-c^2}{4}
3. Định lí sin
Định lí: Trong tam giác ABC bất kỳ, tỉ số giữa một cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là \frac{a}{sin a}=\frac{b}{sin b}=\frac{c}{sin c}=2R với R là bán kính đường tròn ngoại tiếp tam giác
4. Công thức tính diện tích tam giác
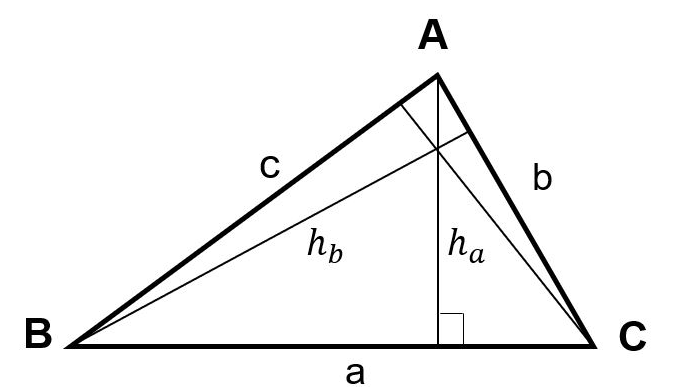
Cho tam giác ABC có
- h_a, h_b, h_c là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB;
- R là bán kính đường tròn ngoại tiếp tam giác;
- r là bán kính đường tròn nội tiếp tam giác;
- p=\frac{a+b+c}{2} là nửa chu vi của tam giác
- S là diện tích tam giác.
Khi đó ta có:
- S=\frac{1}{2}absinC=\frac{1}{2}bcsinA =\frac{1}{2}casinB (1)
- S=\frac{abc}{4R} (2)
- S=pr (3)
- S=\sqrt{p(p−a)(p−b)(p−c)} (công thức Hê – rông) (4)
5. Giải tam giác và ứng dụng vào việc đo đạc
Giải tam giác : Giải tam giác là tìm một số yếu tố của tam giác khi đã biết các yếu tố khác của tam giác đó.
Muốn giải tam giác ta cần tìm mối liên hệ giữa các yếu tố đã cho với các yếu tố chưa biết của tam giác thông qua các hệ thức đã được nêu trong định lí cosin, định lí sin và các công thức tính diện tích tam giác.
1. Cần lưu ý là một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có ít nhất một yếu tố độ dài (tức là yếu tố góc không được quá 2)
2. Việc giải tam giác được sử dụng vào các bài toán thực tế, nhất là các bài toán đo đạc.
II. Bài tập hệ thức lượng trong tam giác và giải tam giác
a) Tính các cạnh của tam giác ABC
b) Tính độ dài các đoạn AH, BH, CH

a) Tính diện tích tam giác ABC theo a
b) Chứng minh a^2+b^2+c^2>=4 \sqrt{3}S

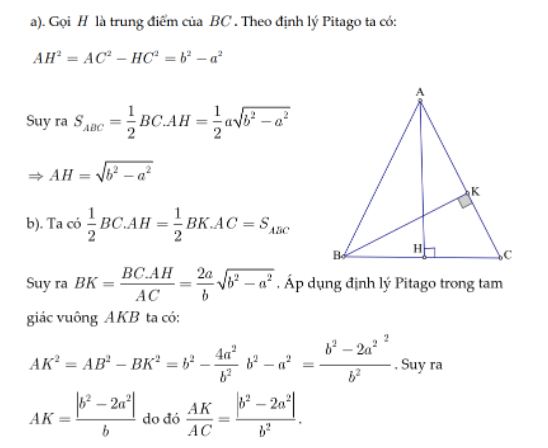
a) Tính diện tích tam giác ABC
b) Dựng BK \bot AC. Tính tỉ số AK/AC

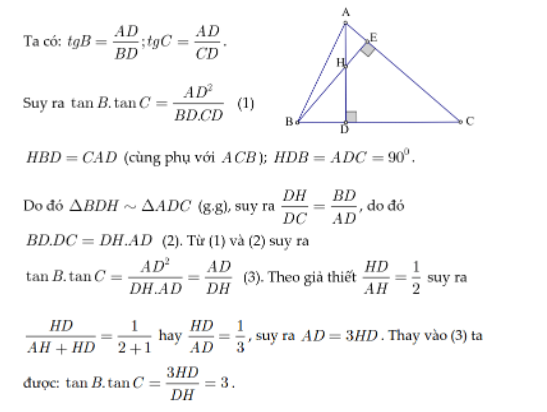
a) Tính độ dài cạnh BC
b) Tính diện tích tam giác ABC


Trên đây là toàn bộ bài viết Hệ thức lượng trong tam giác và giải tam giác – Lý thuyết và bài tập có đáp án. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Hi vọng rằng bài viết sẽ mang lại thêm các kiến thức bổ ích cho các bạn. Hãy đồng hành cùng HocThatGioi để tiếp thu thêm các kiến thức hay, bổ ích nhé. Chúc các bạn học tốt!





