Lý thuyết Phép tịnh tiến đầy đủ nhất
Xin chào các bán, bài học hôm nay sẽ đem đến cho các bạn toàn bộ lý thuyết phép tịnh tiến và một số ví dụ bài tập giúp các bạn rèn luyện. Hãy theo dõi hết bài viết cùng HocThatGioi nhé.
1. Định nghĩa phép tịnh tiến
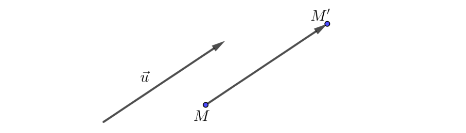
Trong mặt phẳng cho vectơ \overrightarrow{u}, phép tịnh tiến theo vectơ \overrightarrow{u} là phép biến hình biến mỗi điểm M thành điểm M' sao cho \overrightarrow{MM'} = \overrightarrow{u}.
Ký hiệu: T_{\overrightarrow{v}}. Như vậy T_{\overrightarrow{u}}(M) = M' \Leftrightarrow \overrightarrow{MM'} = \overrightarrow{u}
2. Tính chất phép tịnh tiến
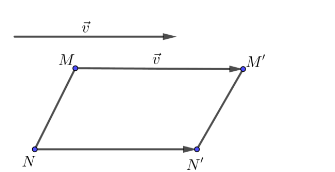
Tính chất 1: Cho \left\{\begin{matrix}T_{\overrightarrow{v}}(M) = M'\\T_{\overrightarrow{v}}(N) = N'\end{matrix}\right. thì \overrightarrow{M'N'} = \overrightarrow{MN}
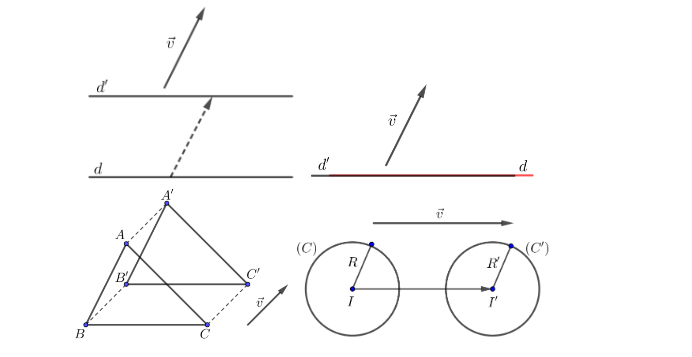
Tính chất 2: Qua phép tinh tiến T_{\overrightarrow{v}}:
- Đường thẳng biến thành đường thẳng song song song hoặc trùng với nó.
- Đoạn thẳng biến thành đoạn thẳng bằng nó.
- Tam giác biến thành tam giác bằng nó.
- Đường tròn biến thành đường tròn có cùng bán kính
– Phép tịnh tiến bảo toàn thứtựcác điểm của đa giác.
– Hai đường thẳng song song có vô sốphép tịnh tiến biến đường này thành đường kia
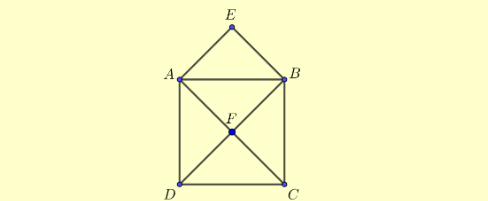
Ta có: \left\{\begin{matrix}T_{\overrightarrow{EA}(B)} = F\\ T_{\overrightarrow{EA}(F)} = D\end{matrix}\right. \Rightarrow T_{\overrightarrow{EA}(BF)} = FD
Xác định T_{\overrightarrow{Ad}(AEB)}
Ta có: \left\{\begin{matrix}T_{\overrightarrow{AD}(A)} = D\\ T_{\overrightarrow{AD}(E)} = F\\T_{\overrightarrow{AD}(B)} = C\end{matrix}\right. \Rightarrow T_{\overrightarrow{AD}(AEB)} = DFC
Xác định T_{\overrightarrow{AE}(ADF)}
Ta có: \left\{\begin{matrix}T_{\overrightarrow{AE}(A)} = E\\ T_{\overrightarrow{AE}(D)} = E\\T_{\overrightarrow{AE}(F)} = B\end{matrix}\right. \Rightarrow T_{\overrightarrow{EA}(BF)} = FD
3. Biểu thức toạ độ
Trong mặt phẳng Oxy, cho điểm M(x;y) và vectơ \overrightarrow{v} = (a;b). Gọi M' là ảnh của M qua phép tính tiến theo vectơ \overrightarrow{v}. Khi đó:
Trong mặt phẳng toá độ Oxy, cho vectơ \overrightarrow{v} = (-1;2)
a. Tìm toạn độ điểm M’ là ảnh của M(3;-2) qua phép T_{\overrightarrow{v}}
b. Tìm toạ độ của điểm N biết T_{\overrightarrow{v}}(N) = N’ và N'(4;1)
T_{\overrightarrow{v}}(M) = M'(x’;y’) \Leftrightarrow \overrightarrow{MM’} = \overrightarrow{v} \Leftrightarrow \left\{\begin{matrix}x’ – 3 = -1\\y’ + 2 = 2\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x’ = 2\\y’ = 0\end{matrix}\right.
Vậy M'(2;0)
b. Tìm toạ độ của điểm N biết T_{\overrightarrow{v}}(N) = N’ và N'(4;1)
T_{\overrightarrow{v}}(N) = N'(x’;y’) \Leftrightarrow \overrightarrow{NN’} = \overrightarrow{v} \Leftrightarrow \left\{\begin{matrix}4 – x = -1\\1 – y = 2\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = 5\\y’ = -1\end{matrix}\right.
Vậy N(5;-1)
Trong mặt phẳng Oxy, cho vectơ \overrightarrow{v} = (-2;-1)
a. Tìm ảnh của đường thẳng d: x – 3y + 5 = 0 qua phép T_{\overrightarrow{v}}.
b. Tìm ảnh của đường tròn (C) = x^{2} + y^{2} – 4x – 2y – 4 = 0 qua phép T_{\overrightarrow{v}}
Gọi M(x;y) \in d: x – 3y + 5 = 0 (1)
T_{\overrightarrow{v}}(M) = M'(x’;y’) \Leftrightarrow \overrightarrow{MM’} = \overrightarrow{v} \Leftrightarrow \left\{\begin{matrix}x’ – x = -2\\y’ – y = – 1\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = x’ + 2\\y = y’ + 1\end{matrix}\right. (2)
Thay (2) và (1) ta được: x’ + 2 – 3(y’ + 1) + 5 = 0 \Leftrightarrow x’ – 3y’ + 4 = 0
b. Tìm ảnh của đường tròn (C) = x^{2} + y^{2} – 4x – 2y – 4 = 0 qua phép T_{\overrightarrow{v}}
Gọi N(x;y) \in (C): x^{2} + y^{2} – 4x – 2y – 4 = 0 (3)
T_{\overrightarrow{v}}(N) = N'(x’;y’) \Leftrightarrow \overrightarrow{NN’} = \overrightarrow{v} \Leftrightarrow \left\{\begin{matrix}x’ – x = -2\\y’ – y = – 1\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = x’ + 2\\y = y’ + 1\end{matrix}\right. (4)
Thay (4) và (3) ta được: (x’ + 2)^{2} + (y’ + 1)^{2} – 4(x’ + 2) – 2(y’ + 1) – 4 = 0\Leftrightarrow x’^{2} + y’^{2} – 9 = 0
Cảm ơn các bạn đã đồng hành cùng HocThatGioi trong bài viết Lý thuyết Phép tịnh tiến đầy đủ nhất. Nếu thấy bài viết này hay, bổ ích hãy chia sẻ cho bạn bè của mình để cùng nhau học giỏi nhé! Chúc các bạn học tốt!





