Phương pháp giải các dạng toán phép quay hay nhất
Xin chào các bạn, sau khi đã năm bắt được toàn bộ lý thuyết phép quay ở bài học trước. Hôm nay HocThatGioi sẽ đem đến cho các ban các dạng bài tập của phép quay và phương pháp để giải các dạng này. Hãy theo dõi hết bài viết cùng HocThatGioi nhé.
1. Tìm toạ độ ảnh của một điểm qua phép quay
Phương pháp 1: Sử dụng định nghĩa
Trong mặt phẳng Oxy. Gọi M'(x_{M};y_{M}) là ảnh của M(x_{M};y_{M}) qua phép quay tâm I(a;b), góc quay \alpha. Khi đó:
Bước 1: Từ (1), sử dụng công thức tính độ dài, sẽ tìm được phương trình thứ nhất chứa 2 ẩn
Bước 2: Từ (2), sủ dụng định láy hàm số \cos, sẽ tìm được phương trình thứ hai theo 2 ẩn
Bước 3: Giải hệ phương trình này tìm được x_{M};y_{M} từ đó suy ra toạ độ điểm M'(x_{M};y_{M})
Phương pháp 2: Sử dụng công thức toạ độ
Phương pháp 3: Trong các trường hợp đơn giản sử dụng hệ trục toạ độ, thực hiện phép quay tìm ngay được toạ độ điểm ảnh.
Trong mặt phẳng Oxy, tìm toạ độ A’, B’ lần lượt là ảnh của A, B qua phép quay tâm O, góc 90^{\circ}. BIết
a. A(1;0)
b. B(0;-2)
Phương pháp 1:
Gọi A’ có toạ độ x’; y’. Khi đó
A'(x’;y’) = Q_{(O;90^{\circ})}(A) \Rightarrow \left\{\begin{matrix}OA = OA’ (1)\\ \widehat{AOA’} = 90^{\circ} (2)\end{matrix}\right.
Từ (1), suy ta (x’)^{2} +(y’)^{2} = 1
Từ (2), suy ra 1.x’ + 0.y’ = 0
Vậy thu được (x’;y’) = (0;1) hoặc (x’;y’) = (0;-1). Vì góc quay dương nên thu được điểm A'(0;1)
b. Xét điểm B(0;-2)
Phương pháp 2:
Gọi B’ có toạ độ là (x’;y’). Khi đó
\left\{\begin{matrix}x’ = (x_{B} – x_{O})cos90^{\circ} – (y_{B} – y_{O}sin90^{\circ}) +x_{O}\\y’ = (x_{B} – x_{O})sin90^{\circ} + (y_{B} – y_{O}cos90^{\circ}) + y_{O}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x’ = 2\\y’ = 0\end{matrix}\right. \Leftrightarrow B'(2;0)
Phương pháp 3: Biểu điểm điểm A, B trên trục toạ độ, có thể suy ra toạ độ điểm A’ và B’
2. Tìm phương trình ảnh của một đường tròn qua phép quay
Phương pháp: Vì phép quay biến đường tròn thành đường tròn có cùng bán kính nên để tìm phương trình ảnh của đường tròn qua phép quay, chúng ta thực hiện qua ba bước sau đây:
- Xác định toạ độ tâm I và bán kính R của đường tròn tạo ảnh từ phương trình đường tròn đã cho.
- Tìm toạ độ tâm I là ảnh của tâm I qua phép quay.
- Viết phương trình đường tròn ảnh với tọa đë tâm I’ và bán kính R.
a. (C): (x – 2)^{2} + (y – 1)^{2} = 1 \alpha = 90^{\circ}
b. (C): x^{2} + y^{2} – 4x – 5 = 0 \alpha = 90^{\circ}
Ta có:
Tâm: I(2;1), R = 1. Suy ra I'(-1;2), R’ = R = 1
(C)’ = (x + 1)^{2} + (y – 2)^{2} = 1
b. (C): x^{2} + y^{2} – 4x – 5 = 0 \alpha = 90^{\circ}
Ta có:
Tâm: I(0;2), R = 3. Suy ra I'(0;2), R’ = R = 3
(C)’ = x^{2} + (y – 2)^{2} = 9
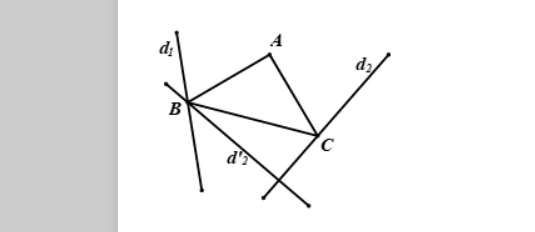
3. Sử dụng phép quay để giải các bài toán dựng hình
Phương pháp: Xem điểm cần dựng là giao của một đường có sẵn và ảnh của một đường khác qua phép quay Q_{I;\alpha} nào đó.
Giả sử đã dựng được tam giác ABC thoả mãn yêu cầu bài toán
Ta có thể giả sử (AB,AC) = 90^{\circ}, khi đó Q_{A, -90^{\circ}}(C) = B mà C \in d_{2} nên B’ \in d_{2}’ với d_{2}’ = Q_{(A;-90^{\circ})}(d_{2})
Ta lại có B \in d_{1} nên B = d_{1} \cap d_{2}’
Cách dựng:
+ Dựng đường thẳng d_{2}’ là ảnh của d_{2} qua Q_{(A;-90^{\circ})}
+ Dựng giao điểm B = d_{1} \cap d_{2}’
+ Dựng đường thẳng qua A vuông góc với AB cắt d_{2} tại C
Tam giác ABC là tam giác cần dựng
Chứng minh: Từ cách dựng suy ra Q_{(a;90^{\circ})}(B) = C nên AB = AC và \widehat{BAC} = 90^{\circ} do đó tam giác ABC vuông cân tại A.
Nhận xét:
+ Nếu d_{1},d_{2} không vuông góc thì bài toán có một nghiệm hình
+ Nếu d_{1} vuông góc d_{2} và A nằm trên đường phân giác của một trong các góc tạo bởi d_{1}, d_{2} thì bài toán có vô số nghiệm hình.
+ Nếu d_{1} vuông góc d_{2} và A không nằm trên đường phân giác của một trong các góc tạo bởi d_{1}, d_{2} thì bài toán vô nghiệm hình.
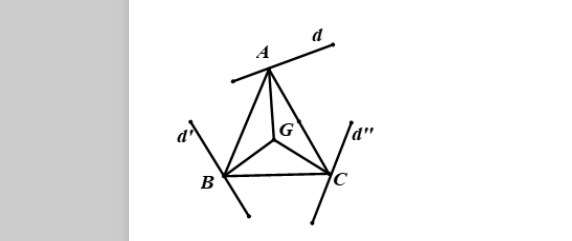
4. Sử dụng phép quay để giải các bài toán tập hợp điểm
Phương pháp: Xem điểm cần dựng là giao của một đường có sẵn và ảnh của một đường khác qua phép quay Q_{(I;\alpha)} nào đó. Để tìm tập hợp điểm M' ta tìm tập hợp điểm M mà Q_{(I;\alpha)} nào đó biến điểm M thành M', khi đó M \in (H) thì M' \in (H') = Q_{(I;\alpha)}((H))
Mà A \in d nên B, C thuộc các đường thẳng là ảnh của d trong hai phép quay nói trên.
Vậy quỹ tích các điểm B, C là các đường thẳng ảnh của d trong hai phép quay tâm G góc quay 120^{\circ} và 240^{\circ}
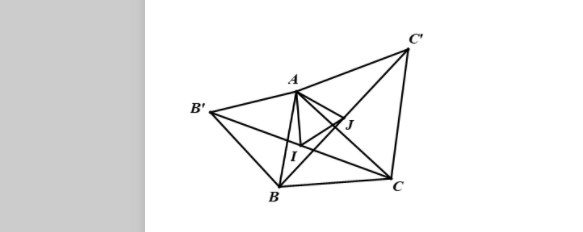
5. Sử dụng phép quay để giải các bài toán hình học phẳng
Xét phép quay Q_{A;60^{\circ}}
Ta có Q_{(A; 60^{\circ})}: B’ -> B, C -> C’ do đó Q_{(A;60^{\circ})}: B’C -> BC’.
Mà I, J lần lượt là trung điểm B’C và BC nên Q_{(A;60^{\circ})}(I) = J.
Vậy nếu I, J không trùng A thì \Delta AIJ đều
Khi \widehat{BAC} = 120^{\circ} thì I \equiv J \equiv A
Trên đây là bài viết Phương pháp giải các dạng toán phép quay hay nhất mà HocThatGioi đã đem đến cho các bạn. Qua bài viết này, Các bạn cùng theo dõi các bài viết tiếp theo về chương phép dời hình, đồng phẳng trong mặt phẳng để có một nền tảng thật vững chắc nhé. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Hãy đồng hành cùng HocThatGioi để tiếp thu thêm các kiến thức hay, bổ ích nhé. Chúc các bạn học tốt





