Tổng hợp các công thức về số bội giác, góc trông của mắt, kính lúp, kính hiển vi và kính thiên văn
Bài viết dưới đây, HocThatGioi sẽ tổng hớp tất cả các công thức về số bội giác , góc trông của mắt, kính lúp, kính hiển vi và kính thiên văn có trong chương Mắt- Các dụng cụ quang học để các bạn tiện theo dõi và áp dụng vào giải toán nhé!
1. Các công thức liên quan đến sự điều tiết của Mắt
Dưới đây, một số công thức cần nhớ để làm bài trong bài toán sự điều tiết của mắt.
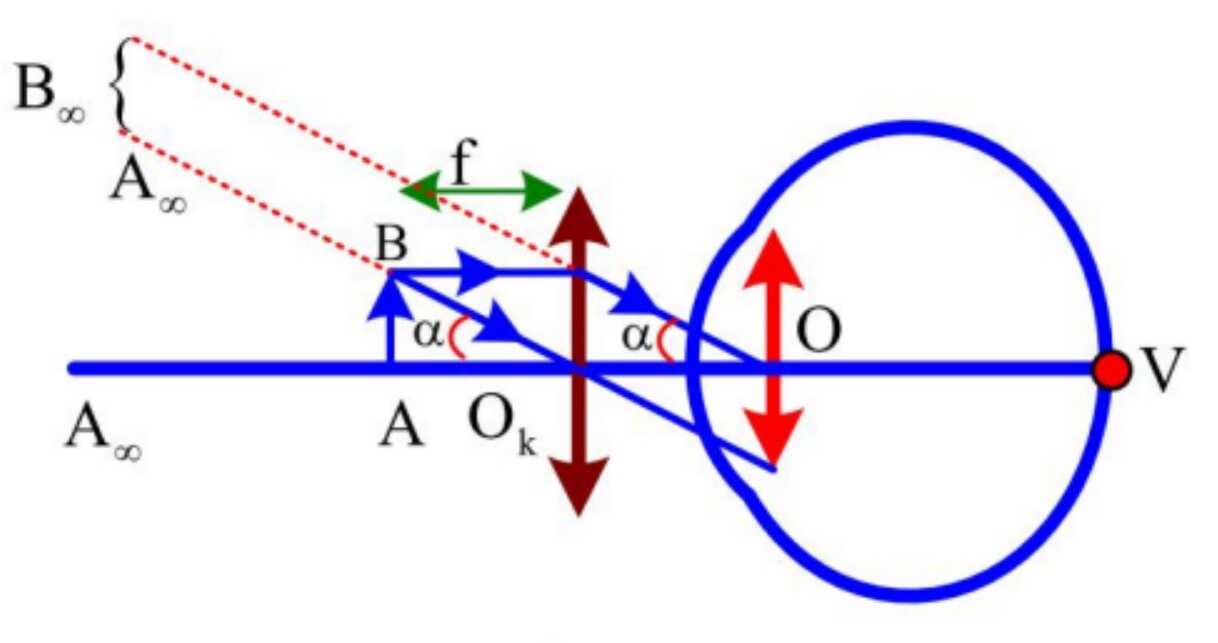
- Độ tụ của mắt khi quan sát trong trạng thái bất kì:
- Độ biến thiên của độ tụ:
D_{max}: khi mắt quan sát trong trạng thái điều tiết tối đa: d= OC_V
D_{min}: khi mắt quan sát trong trạng thái điều không điều tiết: d= OC_V (Mắt không có tật OC_V=\infty)
- Góc trông của vật trực tiếp:
- Sửa tật cận thị:
- Sửa tật viễn thị và lão thị
d’=-(OC_C-l) (2)
Từ (1) và (2) ta có:
\Rightarrow f_K=\frac{d.d’}{d+d’}
2. Các công thức liên quan đến kính lúp
Dưới đây là các công thức như số bội giác, góc trông … của kính lúp các bạn cần chú ý.
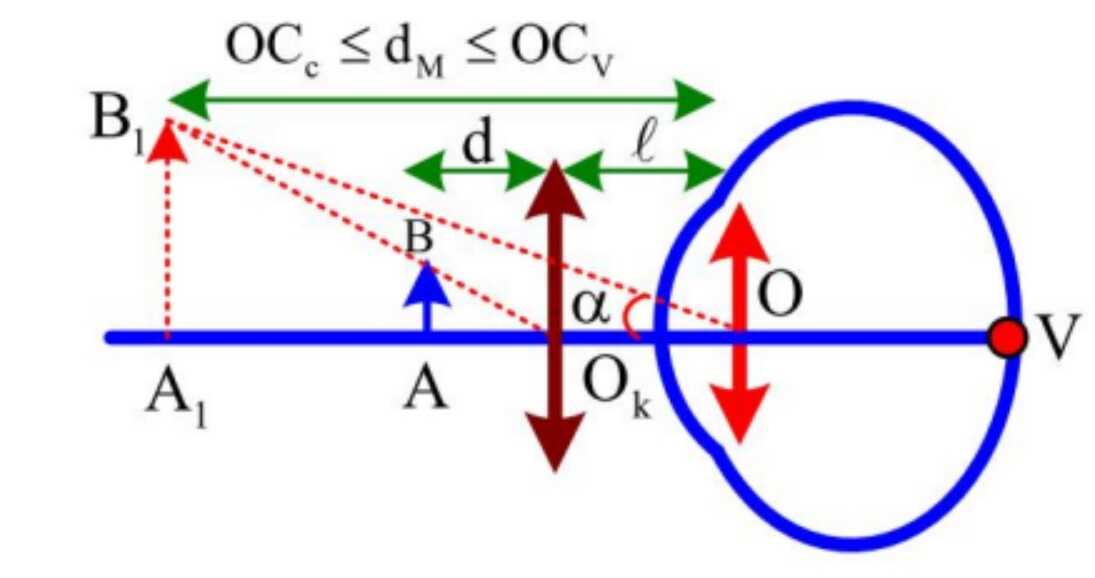
- Ngắm chừng ở cực cận:
\Rightarrow d=\frac{d’.f}{d’-f}
- Ngắm chừng ở cực viễn:
\Rightarrow d=\frac{d’.f}{d’-f}
- Góc trông ảnh tại điểm cực cận:
- Góc trông ảnh A_1B_1 tại điểm bất kì:
- Góc trông khi ngắm chừng ở vô cực:
- Số bội giác của kính lúp:
- Số bội giác khi ngắm chừng ở vô cực:
3. Công thức về số bội giác của kính hiển vi
Dưới đây, công thức về số bội giác, góc trông của kính hiển vi.
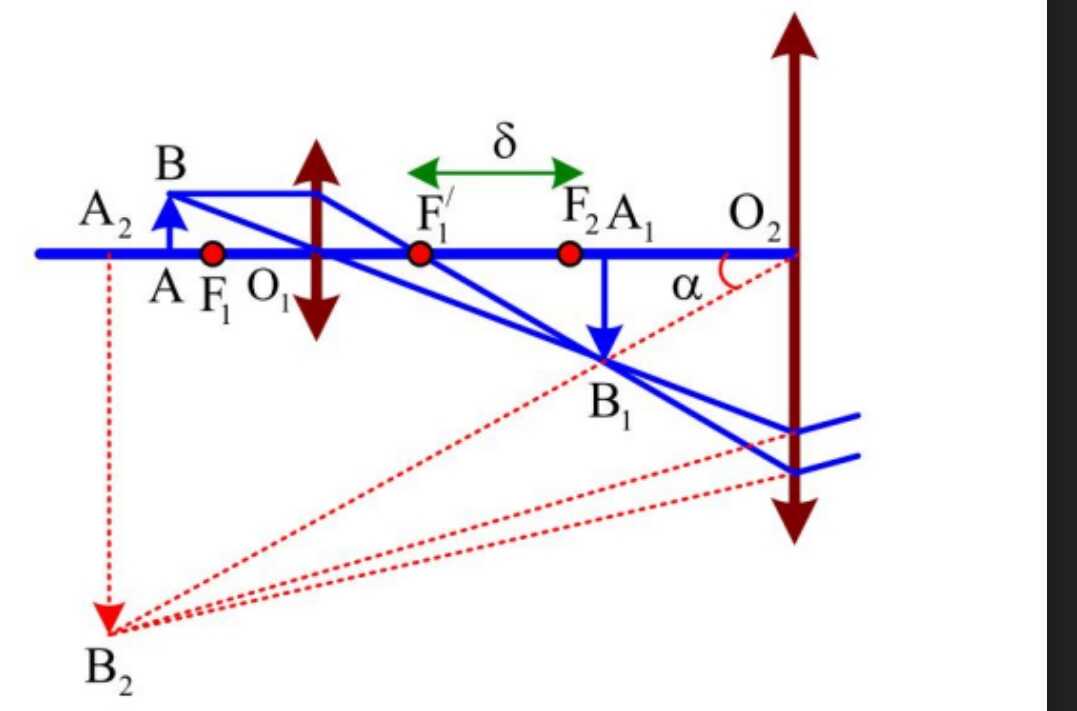
- Số bội giác khi ngắm chừng ở vô cực:
- Số bôi giác tại điểm bất kì:
- Góc trông ảnh tại điểm cực cận:
- Góc trông ảnh A_2B_2 tại điểm bất kì:
4. Công thức của kính thiên văn
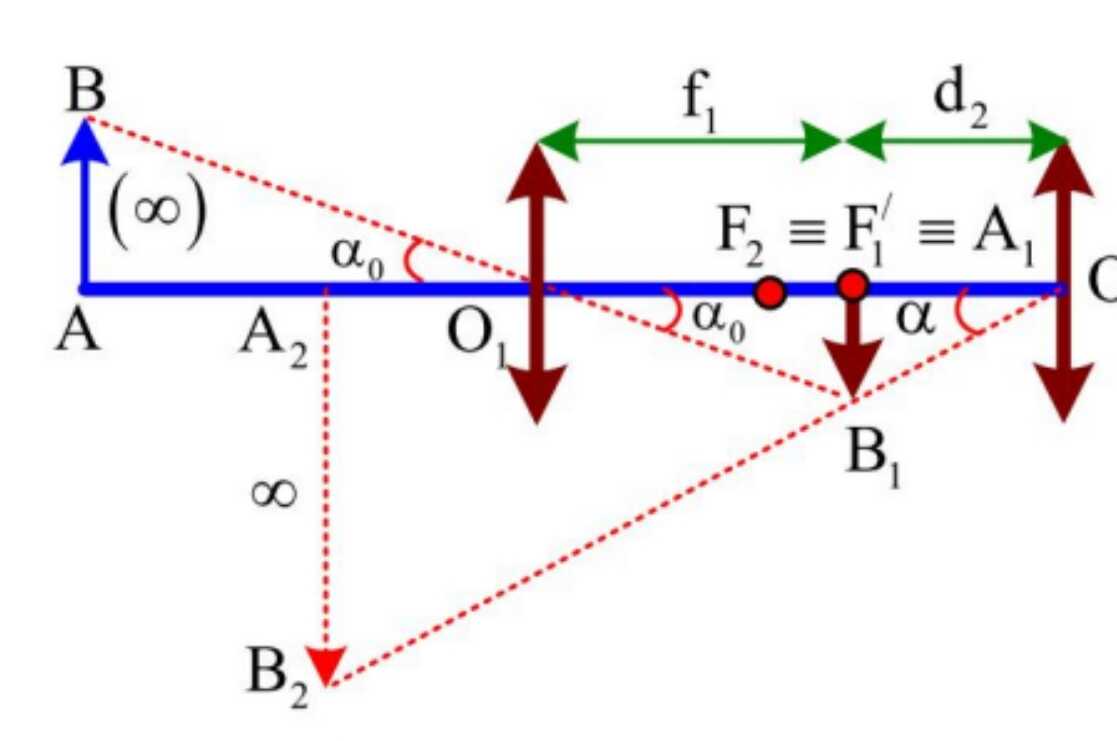
- Độ bội giác của kính thiên văn khi ngắm chức ở vô cực:
Như vậy, bài viết về Tổng hợp các công thức về góc trông, số bội giác của Mắt- Các dụng cụ quang học đến đây đã hết. Qua bài viết, hi vọng các bạn sẽ tiếp thu được nhiều kiến thức hay bổ ích. Đừng quên Like và Share để HocThatGioi ngày càng phát triển. Cảm ơn các bạn đã theo dõi hết bài viết và chúc các bạn học tốt!