Toán 11
Trọn bộ Lý thuyết – Bài tập phép đồng dạng cực hay
Xin chào các bạn, bài học hôm nay sẽ đem đến tới các bạn trọn bộ lý thuyết Phép đồng dạng và cách giải bài toán xác định ảnh trong hệ toạ độ qua Phép đồng dạng cũng như một số bài tập giúp các bạn rèn luyện. Sau khi xem hết bài viết tức là các bạn đã nẵm trọn bộ kiến thức của phép đồng dạng. Vì vậy hãy theo dõi hết bài viết cùng HocThatGioi nhé.
1. Lý thuyết phép đồng dạng
Trước khi bước vào phần bài tập, hãy cùng HocThatGioi theo dõi toàn bộ lý thuyết của phép đồng dạng nhé.
1.1 Định nghĩa
Phép biến hình F được gọi là phép đồng dạng tỉ số k (k > 0) nếu hai điểm M, N bất kì và ảnh M', N' tương ứng chúng ta luôn có MN' = kMN.
Nhận xét:
– Phép dời hình là phép đồng dạng tỉ số 1.
– Phép vị tự tỉ số k là phép đồng dạng tỉ số |k|
– Nếu thực hiện liên tiếp các phép đồng dạng ra được một phép đồng dạng
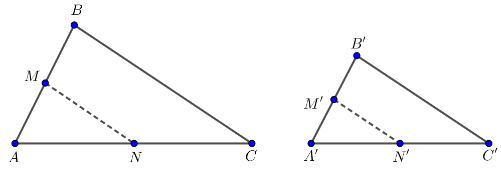
– Phép dời hình là phép đồng dạng tỉ số 1.
– Phép vị tự tỉ số k là phép đồng dạng tỉ số |k|
– Nếu thực hiện liên tiếp các phép đồng dạng ra được một phép đồng dạng
1.2 Tính chất
Phép đồng dạng tỉ số k
- Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy
- Biến đường thẳng thành đường thẳng.
- Biến tia thành tia, biến đoạn thẳng thành đọan thẳng.
- Biến tam giác thành tam giác đồng dạng với nó.
- Biến góc thành góc bằng nó.
- Biến đường tròn bán kính R thành đường tròn bán kính |k|R
1.3 Khái niệm hai hình đồng dạng
Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành hình kia.
2. Bài tập xác định ảnh trong hệ toạ độ qua Phép Đồng Dạng
Phương pháp: Sử dụng định nghĩa, tính chất của phép đồng dạng.
Tiếp theo các bạn hãy làm thành thạo các bài tập tự luận rồi cùng HocThatGioi giải nhanh nhữ câu trắc nghiệm nhé.
2.1 Bài tập tự luận
Bài 01: Trong mặt phẳng Oxy, cho đường thẳng d có phương trình x + y – 2 = 0. Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I(-1;-1) tỉ số k = \frac{1}{2} và phép quay tâm O góc 45^{\circ}
Gọi d_{1} là ảnh của d qua phép vị tự tâm I(-1;1) tỉ số k = \frac{1}{2}.
Vì d_{1} song song hoặc trùng với d nên phương trình có dạng x + y + x = 0
Lấy M(1;2) \in d
Gọi M'(x;y’) = V_{(I;\frac{1}{2})}(M) \Leftrightarrow \overrightarrow{IM’} = \frac{1}{2}\overrightarrow{IM} \Leftrightarrow \left\{\begin{matrix}x + 1 = \frac{1}{2}(1 + 1)\\y + 1 = \frac{1}{2}(1 + 1)\end{matrix}\right. \Leftrightarrow M'(0;0) thuộc d_{1}
Vậy phương trình d_{1}" x + y = 0
Ảnh của d_{1} (đường phân giác góc phần tư thứ hai) qua phép quay tâm O góc 45^{\circ} là đường thẳng Oy
Vậy phương trình của d’ là x = 0
Vì d_{1} song song hoặc trùng với d nên phương trình có dạng x + y + x = 0
Lấy M(1;2) \in d
Gọi M'(x;y’) = V_{(I;\frac{1}{2})}(M) \Leftrightarrow \overrightarrow{IM’} = \frac{1}{2}\overrightarrow{IM} \Leftrightarrow \left\{\begin{matrix}x + 1 = \frac{1}{2}(1 + 1)\\y + 1 = \frac{1}{2}(1 + 1)\end{matrix}\right. \Leftrightarrow M'(0;0) thuộc d_{1}
Vậy phương trình d_{1}" x + y = 0
Ảnh của d_{1} (đường phân giác góc phần tư thứ hai) qua phép quay tâm O góc 45^{\circ} là đường thẳng Oy
Vậy phương trình của d’ là x = 0
Bài 02: Trong mặt phẳng Oxy, cho đường tròn (C): (x – 1)^{2} + (y – 2)^{2} = 9. Ảnh của đường tròn (C) qua phép đồng dạng có được bằng cách thực hiên liên tiếp phép vị tự tâm I(1;-1) tỉ số k = \frac{1}{3} và phép tịnh tiến theo vectơ \overrightarrow{v} = (3;4) có phương trình là
Gọi M(1;2); R = 3 là tâm và bán kính đường tròn (C)
V_{(I;k)}(M) = O’ \Leftrightarrow \overrightarrow{IO’} = \frac{1}{3}\overrightarrow{IM} \Rightarrow O'(1;0)
Phép vị tự biến đường tròn tâm M thành đường tròn O’ bán kính R’ = \frac{1}{3}R = 1. T_{\overrightarrow{v}}(O’) = O” \Rightarrow O”(4;4)
Phép tịnh tiến theo vectơ \overrightarrow{v} biến đường tròn O’ bán kính R’ thành đường tròn tâm O” bán kính R” = R’ = 1
Vậy phương trình đường tròn ảnh: (x – 4)^{2} + (y – 4)^{2} = 1
V_{(I;k)}(M) = O’ \Leftrightarrow \overrightarrow{IO’} = \frac{1}{3}\overrightarrow{IM} \Rightarrow O'(1;0)
Phép vị tự biến đường tròn tâm M thành đường tròn O’ bán kính R’ = \frac{1}{3}R = 1. T_{\overrightarrow{v}}(O’) = O” \Rightarrow O”(4;4)
Phép tịnh tiến theo vectơ \overrightarrow{v} biến đường tròn O’ bán kính R’ thành đường tròn tâm O” bán kính R” = R’ = 1
Vậy phương trình đường tròn ảnh: (x – 4)^{2} + (y – 4)^{2} = 1
Bài 03. Trong mặt phẳng toạ độ Oxy, cho đường tròn (C): (x – 2)^{2} + (y + 1)^{2} = 9. Gọi (C”) là ảnh của đường tròn (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = -\frac{1}{3} và phép tịnh tiến theo vectơ \overrightarrow{v} = (-1;3). Tìm bán kính của đường tròn (C’)
Đường tròn (C) có bán kính R = 3
Gọi (C_{1}) là ảnh của đường tròn (C) qua phép vị tự tâm O, tỉ số k = -\frac{1}{3}, ta có (C’) là ảnh của (C_{1}) qua phép tịnh tiến theo vectơ \overrightarrow{v} = (-1;3)
Khi đó đường tròn (C_{1}) có bán kính R_{1} = |k|R = \frac{1}{3}.3 = 1 và đường tròn (C’) có bán kính R’ = R = 1
Gọi (C_{1}) là ảnh của đường tròn (C) qua phép vị tự tâm O, tỉ số k = -\frac{1}{3}, ta có (C’) là ảnh của (C_{1}) qua phép tịnh tiến theo vectơ \overrightarrow{v} = (-1;3)
Khi đó đường tròn (C_{1}) có bán kính R_{1} = |k|R = \frac{1}{3}.3 = 1 và đường tròn (C’) có bán kính R’ = R = 1
Bài 04. Trong mặt phẳng với hệ trục toạ độ Oxy cho đường tròn (C_{1}): x^{2} + y^{2} – 2x – 2y – 2 = 0 và (C_{2}): x^{2} + y^{2} + 12x – 16y = 0. Phép đồng dạng F tỉ số k biến (C_{1}) thành (C_{2}). Tìm k
Ta có (C_{1}): x^{2} + y^{2} – 2x – 2y – 2 = 0 \Leftrightarrow (x – 1)^{2} + (y – 1)^{2} = 2^{2}
Suy ra (C_{1}) có bán kính R_{1} = 2. (C_{2}) : x^{2} + y^{2} + 12x – 16y = 0 \Leftrightarrow (x + 6)^{2} + (y – 8)^{2} = 10^{2}
Suy ra (C_{2}) có bán kính R_{2} = 10. Do đó k = \frac{R_{2}}{R_{1}} = 5
Suy ra (C_{1}) có bán kính R_{1} = 2. (C_{2}) : x^{2} + y^{2} + 12x – 16y = 0 \Leftrightarrow (x + 6)^{2} + (y – 8)^{2} = 10^{2}
Suy ra (C_{2}) có bán kính R_{2} = 10. Do đó k = \frac{R_{2}}{R_{1}} = 5
Bài 05. Trong mặt phăngr toạ độ Oxy cho đường thẳng d có phương trình x + y – 2 = 0. Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I(-1;-1) tỉ số k = \frac{1}{2} và phép quay O góc -45^{\circ}
Xét điểm A(1;1) và B(2;0) nằm trên đường thẳng d.
Qua phép vị tự tâm I(-1;-1) điểm A biến thành điểm A’ với toạ độ thoả mãn \left\{\begin{matrix}x_{A’} + 1 = \frac{1}{2}(x_{A} + 1)\\y_{A’} + 1 = \frac{1}{2}(y_{A} + 1)\end{matrix}\right.. Vậy A'(0;0)
Qua phép quay tâm O góc -45^{\circ}, điểm A’ biến thành điểm A”(0;0).
Qua phép vị tự tâm I(-1;-1) điểm B biến thành điểm B’ với toạ độ thoả mãn
\left\{\begin{matrix}x_{B’} + 1 = \frac{1}{2}(x_{B} + 1)\\y_{B’} + 1 = \frac{1}{2}(y_{B} + 1)\end{matrix}\right.. Vậy B'(\frac{1}{2};-\frac{1}{2})
Qua phép quay tâm O góc -45^{\circ} biến điểm B’ thành điểm B” với toạ độ thoả mãn:
\left\{\begin{matrix}x_{B”} = cos(-45^{\circ}).x_{B’} – sin(-45^{\circ}).y_{B’}\\y_{B”} = sin(-45^{\circ}).x_{B’} + cos(-45^{\circ})y_{B’}\end{matrix}\right.. Vậy B”(0;\frac{\sqrt{2}}{2})
Do đó đường thẳng d biến thành đường thẳng A”B” có phương trình x = 0
Qua phép vị tự tâm I(-1;-1) điểm A biến thành điểm A’ với toạ độ thoả mãn \left\{\begin{matrix}x_{A’} + 1 = \frac{1}{2}(x_{A} + 1)\\y_{A’} + 1 = \frac{1}{2}(y_{A} + 1)\end{matrix}\right.. Vậy A'(0;0)
Qua phép quay tâm O góc -45^{\circ}, điểm A’ biến thành điểm A”(0;0).
Qua phép vị tự tâm I(-1;-1) điểm B biến thành điểm B’ với toạ độ thoả mãn
\left\{\begin{matrix}x_{B’} + 1 = \frac{1}{2}(x_{B} + 1)\\y_{B’} + 1 = \frac{1}{2}(y_{B} + 1)\end{matrix}\right.. Vậy B'(\frac{1}{2};-\frac{1}{2})
Qua phép quay tâm O góc -45^{\circ} biến điểm B’ thành điểm B” với toạ độ thoả mãn:
\left\{\begin{matrix}x_{B”} = cos(-45^{\circ}).x_{B’} – sin(-45^{\circ}).y_{B’}\\y_{B”} = sin(-45^{\circ}).x_{B’} + cos(-45^{\circ})y_{B’}\end{matrix}\right.. Vậy B”(0;\frac{\sqrt{2}}{2})
Do đó đường thẳng d biến thành đường thẳng A”B” có phương trình x = 0
2.2 Bài tập trắc nghiệm
1. Mệnh đề nào sau đây sai ?
2. Mệnh đề nào sau đây sai ?
3. Cho tam giác ABC và A’B’C’ đồng dạng với nhau theo tỉ số k. Mệnh đề nào sau đây sai ?
4. Mọi phép dời hình cũng là phép đồng dạng tỉ số k bằng
5. Mệnh đề nào sau đây sai?
6. Trong mặt phẳng Oxy, cho điểm M(2;4). Phép đồng dnagj có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = \frac{1}{2} và phép đối xứng trục Oy sẽ biến điểm M thành điểm nào sau đây ?
7. Trong mặt phẳng Oxy, cho đường thẳng d có phương trình x + y – 2 = 0. Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I(-1;-1) tỉ số k = \frac{1}{2} và phép quay tâm O góc -45^{\circ}
8. Trong mặt phẳng Oxy, cho đường tròn (C) có phương trinh (x – 2)^{2} + (y – 2)^{2} = 4. Phép đồng dnagj có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = \frac{1}{2} và phép quay tâm O góc 90^{\circ} sẽ biến (C) thành đường tròn nào sau đây ?
9. Trong mặt phẳng Oxy, cho hai điểm A(-2;-3), B(4;1). Phép đồng dạng có tỉ số k = \frac{1}{2} biến điểm A thành A’ biến điểm B thành B’. Tính độ dài A’B’
10. Trong mặt phẳng Oxy, cho hai đường tròn (C) và (C’) có phương trình x^{2} + y^{2} – 4y – 5 = 0 và x^{2} + y^{2} – 2x + 2y – 14 = 0. Gọi (C’) là ảnh của (C) qua phép đồng dạng tỉ số k. Khi đó k có giá trị là
Như vậy, bài viết Trọn bộ Lý thuyết – Bài tập phép đồng dạng cực hay của HocThatGioi đến đây đã hết. Qua bài viết, hi vọng giúp các bạn tổng ôn được các kiến thức trọng tâm. Đừng quên Like và Share để HocThatGioi ngày càng phát triển nhé! Cảm ơn các bạn đã theo dõi hết bài viết và chúc các bạn học tốt!
