Giải SGK bài 24 chương VIII trang 66, 67, 68, 69, 70, 71 Toán 10 Kết nối tri thức tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Hoán vị, chỉnh hợp và tổ hợp. Đây là bài học thuộc bài 24 chương VIII trang 66, 67, 68, 69, 70, 71 sách Toán 10 Kết nối tri thức tập 2. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi trong SGK của bài 24
Dưới đây là phương pháp và bài giải chi tiết cho câu hỏi mở đầu, câu hỏi hoạt động, vận dụng cùng phần luyện tập ở các trang 66, 67, 68, 69, 70 trong bài Hoán vị, chỉnh hợp và tổ hợp. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Câu hỏi mở đầu trang 66
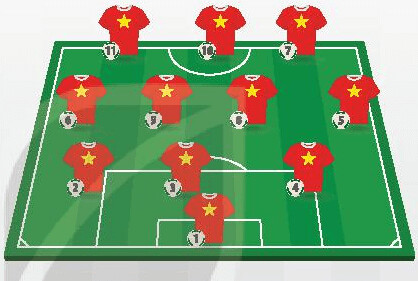
Sau khi học xong bài này, ta giải quyết bài toán trên như sau:
Vì mỗi đội hình gồm có 1 thủ môn, 3 hậu vệ, 4 tiền vệ và 3 tiền đạo và đã biết trước vị trí thủ môn, nên để chọn đội hình ta cần thực hiện 3 công đoạn:
1. Chọn hậu vệ là chọn 3 trong số 7 hậu vệ: có $C_7^3=35$ (cách).
2. Chọn tiền vệ là chọn 4 trong số 8 tiền vệ: có $C_8^4=70$ (cách).
3. Chọn tiền đạo là chọn 3 trong số 5 tiền đạo: có $C_5^3=10$ (cách).
Vậy, theo quy tắc nhân, số các đội hình có thể có (khi đã biết vị trí thủ môn) là $35 . 70. 10=24500$ (đội hình).
Hoạt động 1 trang 66

a) Hãy liệt kê ba cách sắp xếp bốn bạn trên theo thứ tự.
b) Có bao nhiêu cách sắp xếp thứ tự bốn bạn trên để tham gia phỏng vấn?
a) Ba cách sắp xếp bốn bạn trên theo thứ tự:
– Hà, Mai, Nam, Đạt.
– Hà, Mai, Đạt, Nam
– Hà, Đạt, Mai, Nam
Chú ý: Có thể chọn các cách xếp khác, không nhất thiết phải giống trên.
b) Ta thực hiện các bước:
– Chọn bạn đứng đầu có 4 cách
– Chọn bạn đứng thứ hai có 3 cách
– Chọn bạn đứng thứ ba có 2 cách
– Chọn bạn đứng cuối có 1 cách
Vậy có $4.3 .2=24$ cách sắp xếp thứ tự bốn bạn trên để tham gia phỏng vấn.
Luyện tập 1 trang 67
Số các hoán vị của tập hợp có n phần tử là n!
Số cách sắp xếp 6 vận động viên vào 6 đường chạy là số hoán vị của 6 phần tử.
=> Số cách xếp các vận động viên vào các đường chạy đó là:
$$\text { 6!= } 720 \text { cách }$$
Hoạt động 2 trang 67
a) Giáo viên cần chọn ra hai bạn phụ trách nhóm trên. Hỏi có bao nhiêu cách chọn hai bạn từ 4 bạn trên?
b) Có bao nhiêu cách chọn hai bạn, trong đó một bạn làm nhóm trưởng, một bạn làm nhóm phó?
a)
Bước 1: Chọn 1 bạn từ 4 bạn trên: có 4 cách
Bước 2: Chọn 1 bạn từ 3 bạn còn lại
Do hai bạn có vai trò như nhau nên ta chia kết quả cho 2 để loại trường hợp trùng.
Có $(4.2):2=6$ cách chọn hai bạn từ 4 bạn trên.
b)
Chọn nhóm trưởng: có 4 cách
Chọn nhóm phó: có 3 cách
Theo quy tắc nhân, có $4.3= 12$ cách chọn hai bạn, trong đó một bạn làm nhóm trưởng, một bạn làm nhóm phó.
Luyện tập 2 trang 68
Mỗi cách chọn lần lượt 3 trong số 12 con ngựa để trao giải nhất, nhì, ba là một chỉnh hợp chập 3 của 12.
Số kết quả xảy ra là: $A_{12}^3=1320$ (kết quả)
Hoạt động 3 trang 68
a) Hãy cho biết sự khác biệt khi chọn ra hai bạn ở câu HĐ2a và HĐ2b.
b) Từ kết quả tính được ở câu HĐ2b (áp dụng chỉnh hợp), hãy chỉ ra cách tính kết quả ở câu HĐ2a.
a) Hai bạn được chọn ở HĐ2a có vai trò như nhau, nói cách khác là không quan trọng thứ tự chọn.
Còn ở HĐ2b thì hai bạn có có vai trò khác nhau, nói cách khác là có xếp thứ tự lần lượt là lớp trưởng và lớp phó.
b) Số cách chọn 2 bạn (có xếp thứ tự) là 12 cách chọn.
Nhưng ở HĐ2a thì hai bạn có vai trò như nhau nên ta chia kết quả cho 2, tức là có 6 cách chọn (khi không xếp thứ tự)
Luyện tập 3 trang 69
Áp dụng công thức tổ hợp và quy tắc nhân.
Số cách chọn 2 trong 20 câu lí thuyết là: $C_{20}^2$
Số cách chọn ra 3 trong 40 câu bài tập là: $C_{40}^3$
=> Số cách lập đề thi gồm 5 câu hỏi như trên là: $C_{20}^2.C_{40}^3=1877200$
Vận dụng trang 70
a) Có bao nhiêu cách chọn 6 thành viên vào Ban quản lí?
b) Có bao nhiêu cách chọn Trưởng ban, 1 Phó ban, 4 thành viên khác vào ban quản lí?
a) Áp dụng công thức tổ hợp.
b) Áp dụng quy tắc nhân và công thức tổ hợp.
a) Số cách chọn 6 trong 20 học sinh vào Ban quản lí là: $C_{20}^6=38760$
b)
– Chọn Trưởng ban có $20$ cách.
– Chọn 1 Phó ban có $19$ cách.
– Chọn 4 trong 18 thành viên còn lại vào ban quản lí có: $C_{18}^4$ cách
Vậy có tất cả số cách là: $20.19. C_{18}^4=1162800$
Giải bài tập vận dụng trang 70, 71 SGK Toán 10 bài 24
Phần tiếp theo sẽ cung cấp cho các bạn phương pháp cùng lời giải trong phần bài tập trang 70, 71 cực kỳ dễ hiểu và chi tiết. Cùng HocThatGioi rèn luyện và nâng cao kỹ năng giải quyết các vấn đề thực tế thông qua các phương pháp, công thức toán học từ bài Hoán vị, chỉnh hợp và tổ hợp ở trên.
Bài tập 8.6 trang 70
Áp dụng công thức hoán vị
Mỗi cách xếp 10 bức tranh thành một hàng ngang là một hoán vị của 10.
Số cách để họa sĩ sắp xếp các bức tranh là $10!= 3 628 800$
Bài tập 8.7 trang 70
Áp dụng quy tắc nhân.
Từ 4 chữ số $0, 1, 2, 3, 4$ ta chọn:
– Chữ số hàng trăm có $4$ cách ( khác 0)
– Chữ số hàng nghìn có $4$ cách.
– Chữ số hàng đơn vị có $3$ cách
Vậy có thể lập được $4. 4. 3= 48$ số tự nhiên có ba chữ số khác nhau.
Bài tập 8.8 trang 70
Áp dụng công thức tổ hợp.
Có tất cả 99 số nguyên dương nhỏ hơn 100.
Số cách chọn một tập hợp gồm hai trong 99 số đó là: $C_{99}^2=4581$
Số cách chọn một tập hợp gồm ba số trong 99 số đó là: $C_{99}^3=156849$
Bài tập 8.9 trang 70
Áp dụng quy tắc nhân.
Số cách để Hà chọn ra đúng 2 viên bi khác màu là: $5. 7 = 35$ (cách)
Bài tập 8.10 trang 71
a) Có bao nhiêu cách chọn 4 bạn nam?
b) Có bao nhiêu cách chọn 4 bạn không phân biệt nam, nữ?
c) Có bao nhiêu cách chọn 4 bạn, trong đó có 2 bạn nam và 2 bạn nữ?
Áp dụng công thức tổ hợp và quy tắc nhân.
a) Số cách chọn 4 bạn trong 10 bạn nam là: $C_{10}^4=210$ (cách)
b) Số cách chọn 4 bạn trong tổng 17 bạn (không phân biệt nam, nữ) là: $C_{17}^4=2380$ (cách)
c) Số cách chọn 4 bạn, trong đó có 2 bạn nam và 2 bạn nữ là: $C_{10}^2 . C_7^2=45.21=945$ (cách)
Bài tập 8.11 trang 71
Áp dụng công thức chỉnh hợp và quy tắc nhân.
– Trường hợp 1: Chữ số hàng đơn vị là 0.
Mỗi cách chọn 3 số (có xếp thứ tự ) trong 9 số còn lại là một chỉnh hợp chập 3 của 9.
Số cách chọn 3 chữ số còn lại là $A_9^3=504$
– Trường hợp 2: Chữ số hàng đơn vị là 5.
Số cách chọn chữ số hàng nghìn là 8 ( khác 0 )
Số cách chọn 2 trong chữ số (có xếp thứ tự) trong 8 số còn lại là: $A_8^2=56$
Vậy có: $504+ (8.56)=952$ số tự nhiên chia hết cho 5 mà mỗi số có bốn chữ số khác nhau.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Hoán vị, chỉnh hợp và tổ hợp Chương Đại số tổng hợp Toán 10 Kết nối tri thức tập 2 ở các trang 66, 67, 68, 69, 70, 71. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!





