Giải SGK bài 25 Nhị thức Newton trang 72, 73, 74, 75 Toán 10 Kết nối tri thức Tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Nhị thức Newton. Đây là bài học thuộc bài 25 chương VIII trang 72, 73, 74, 75 sách Toán 10 Kết nối tri thức tập 2. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi trong SGK của bài 25
Dưới đây là phương pháp và bài giải chi tiết cho câu hỏi mở đầu, câu hỏi hoạt động, vận dụng cùng phần luyện tập ở các trang 72, 73, 74 trong bài Nhị thức Newton. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Câu hỏi mở đầu trang 72
(a+b)^2=a^2+2 a b+b^2 \\\\ (a+b)^3=a^3+3 a^2 b+3 a b^2+b^3
Quan sát các đơn thức ở vế phải của các đằng thức trên, hãy nhận xét về quy luật số mũ của $a$ và $b$. Có thể tìm được cách tính các hệ số của đơn thức trong khai triển $(a+b)^n$ khi $n \in\{4 ; 5\}$ không?
– Ta có:
a^2+2 a b+b^2=a^2a^2.b^0+2.a^1.b^1+b^2.a^0 \\\\ a^3+3 a^2 b+3 a b^2+b^3=a^3.b^0+3.a^2.b^1+3.a^1. b^2+a^0.b^3
Quan sát vế phải của các đẳng thức, ta thấy số mũ của a giảm dần từ số mũ của biểu thức vế trái đến 0 , còn số mũ của b tăng dần từ 0 đến số mũ của biểu thức ở vế trái.
– Sau khi học bài Nhị thức Newton này, ta có thể tìm được cách tính các hệ số của đơn thức trong khai triển $(a+b)^n$ khi $n \in\{4 ; 5\}$.
Hoạt động 1 trang 72
– Từ một đểm gốc, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức (gọi là nhãn của mũi tên) của nhị thức thứ nhất $(\mathrm{H} .8 .6)$;
– Từ ngọn của mỗi mũi tên đã xây dựng, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức của nhị thức thứ hai;
– Tại ngọn của các mũi tên xây dựng tại bước sau cùng, ghi lại tích của các nhãn của các mũi tên đi từ điểm gốc đến đầu mút đó.
Hãy lấy tổng của các tích nhận được và so sánh kết quả với khai triển của tích $(a+b) \cdot(c+d)$.
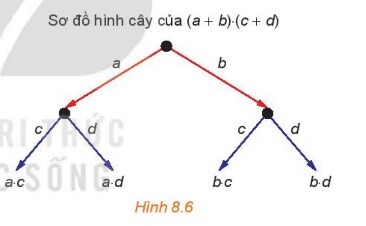
Tổng các tích nhận được bằng với kết quả khai triển của tích $(a+b).(c+d)= a.c+a.d+b.c+b.d$
Hoạt động 2 trang 72
Có bao nhiêu tích nhận được lần lượt bằng $a^{3}, a^{2} b, a b^{2}, b^{3}$ ?
Hãy so sánh chúng với các hệ số nhận được khi khai triển $(a+b)^{3}$.
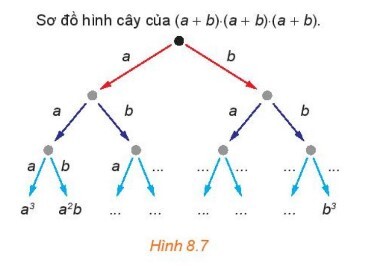
Các đơn thức còn thiếu hàng trên lần lượt là: $b, a, b, a, b$.
Hàng dưới lần lượt là: $a^2 b, a b^2, a^2 b, a b^2, a b^2$
Ta có: $(a+b)^3=a^3+3 a^2 b+3 a b^2+b^3$
Các hệ số nhận được khi khai triển là bằng nhau.
Hoạt động 3 trang 73
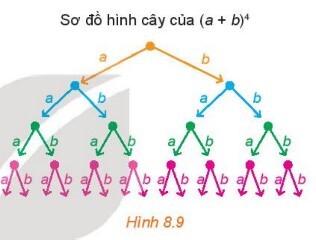
Lập luận tương tự trên, dùng kiến thức về tổ hợp, hãy cho biết trong tổng nêu trên, có bao nhiêu đơn thức đồng dạng với mỗi đơn thức thu gọn sau:
$a^4 ; \quad a^3 b ; \quad a^2 b^2 ; \quad a b^3 ; \quad b^4 ?$
Số đơn thức đồng dạng với $a^4$ trong tổng là $C_4^0=1$
Số đơn thức đồng dạng với $a^3 b$ trong tổng là $C_4^4=1$
Số đơn thức đồng dạng với $a^2 b^2$ trong tổng là $C_4^2=6$
Số đơn thức đồng dạng với $a b^3$ trong tổng là $C_4^3=1$
Số đơn thức đồng dạng với $b^4$ trong tổng là $C_4^4=1$
Luyện tập 1 trang 73
Áp dụng công thức khai triển $(a+b)^4=a^4+4 a^3 b+6 a^2 b^2+4 a b^3+b^4$ với $\mathrm{a}=\mathrm{x}, \mathrm{b}=-2$.
(x-2)^4 \\\\ =x^4+4.x^3.(-2)+6.x^2.(-2)^2+4.x.(-2)^3+(-2)^4 \\\\ =x^4-8 x^3+24 x^2-32 x+16
Hoạt động 4 trang 74
Lập luận tương tự trên, dùng kiến thức về tổ hợp, hãy cho biết trong tổng nêu trên, có bao nhiêu đơn thức đồng dạng với mỗi đơn thức thu gọn sau:
$a^5$ ; $ \quad a^4 b$; $ \quad a^3 b^2$; $ \quad a^2 b^3$; $\quad a b^4$; $\quad b^5 ?$
Số đơn thức đồng dạng với $a^5$ trong tổng là $C_5^0=1$
Số đơn thức đồng dạng với $a^4 b$ trong tổng là $C_5^1=5$
Số đơn thức đồng dạng với $a^3 b^2$ trong tổng là $C_5^2=10$
Số đơn thức đồng dạng với $a^2 b^3$ trong tổng là $C_5^3=10$
Số đơn thức đồng dạng với $a b^4$ trong tổng là $C_5^4=5$
Số đơn thức đồng dạng với $b^5$ trong tổng là $C_5^5=1$
Luyện tập 2 trang 74
Áp dụng công thức khai triển $(a+b)^5=a^5+5 a^4 b+10 a^3 b^2+10 a^2 b^3+5 a b^4+b^5$ với $a=3 \mathrm{x}, \mathrm{b}=-2$
Ta có: $(3 x-2)^5$
=(3 x)^5+5.(3 x)^4.(-2)+10.(3 x)^3.(-2)^2 +10.(3 x)^2.(-2)^3+5.3 x.(-2)^4+(-2)^5 \\\\ =243 x^5-810 x^4+1080 x^3-720 x^2+240 x-32
Vận dụng trang 74
b) Dùng máy tính cầm tay tính giá trị của $1,05^4$ và tính sai số tuyệt đối của giá trị gần đúng nhận được ở câu a.
a) Áp dụng công thức khai triển:
$$(a+b)^4=a^4+4 a^3 b+6 a^2 b^2+4 a b^3+b^4$$
b) Lấy kết quả tính bằng máy tính trừ đi kết quả câu a để tính sai số tuyệt đối.
a) Giá trị gần đúng của $1,05^4$ là: $1^4+4.1^3.0,05=1,2$
b) $1,05^4=1,2155$
Sai số tuyệt đối là: $1,2155-1,2=0,0155$
Giải bài tập vận dụng trang 74, 75 SGK Toán 10 bài 25
Phần tiếp theo sẽ cung cấp cho các bạn phương pháp cùng lời giải trong phần bài tập trang 74, 75 cực kỳ dễ hiểu và chi tiết. Cùng HocThatGioi rèn luyện và nâng cao kỹ năng giải quyết các vấn đề thực tế thông qua các phương pháp, công thức toán học từ bài Nhị thức Newton ở trên.
Bài tập 8.12 trang 74
a) $(x-3)^{4}$
b) $(3 x-2 y)^{4}$;
c) $(x+5)^{4}+(x-5)^{4}$;
d) $(x-2 y)^{5}$
Áp dụng công thức khai triển:
$(a+b)^4=a^4+4 a^3 b+6 a^2 b^2+4 a b^3+b^4$ và $(a+b)^5=a^5+5 a^4 b+10 a^3 b^2+10 a^2 b^3+5 a b^4+b^5$
a) $(x-3)^4=x^4+4 x^3.(-3)+6 x^2 .(-3)^2+4 x.(-3)^3+(-3)^4$
$=x^4-12 x^3+54 x^2-108 x+81$
b) $(3 x-2 y)^4=81 x^4-216 x^3 y+216 x^2 y^2-96 x y^3+16 y^4$
c) (x+5)^4+(x-5)^4 \\\\ =x^4+20 x^3+150 x^2+500 x+625 +x^4-20 x^3+150 x^2-500 x+625 \\\\ =2 x^4+300 x^2+1250
d) $(x-2 y)^5=x^5-10 x^4 y+40 x^3 y^2-80 x^2 y^3+80 x y^4-32 y^5$
Bài tập 8.13 trang 74
Áp dụng công thức khai triển $(a+b)^5=a^5+5 a^4 b+10 a^3 b^2+10 a^2 b^3+5 a b^4+b^5$
Hệ số của $x^4$ trong khai triển của $(3 x-1)^5$ là:
$C_5^1.3^4.(-1)=-405$
Bài tập 8.14 trang 74
Áp dụng công thức khai triển $(a+b)^5=a^5+5 a^4 b+10 a^3 b^2+10 a^2 b^3+5 a b^4+b^5$
(3+ \sqrt{2})^5-(3- \sqrt{2})^5 \\\\ = 3^5+5.3^4+\sqrt{2}+10.3^3(\sqrt{2})^2+10.3^2(\sqrt{2})^3+5.3(\sqrt{2})^4+\sqrt{2}^5-(3^5-5.3^4.\sqrt{2}+10.3^3(\sqrt{2})^2-10.3^2(\sqrt{2})^3+5.3(\sqrt{2})^4-\sqrt{2}^5) \\\\ =2(5.3^4.\sqrt{2}+10.3^2(\sqrt{2})^3+\sqrt{2}^5) \\\\ =810 \sqrt{2}+360 \sqrt{2}+8 \sqrt{2} \\\\ = 1178 \sqrt{2}
Bài tập 8.15 trang 75
b) Dùng máy tính cầm tay tính giá trị của $1,02^5$ và tính sai số tuyệt đối của giá trị gần đúng nhận được ở câu a.
Áp dụng công thức khai triển
$$(a+b)^5=a^5+5 a^4 b+10 a^3 b^2+10 a^2 b^3+5 a b^4+b^5$$
Lấy kết quả tính bằng máy tính trừ đi kết quả câu a để tính sai số tuyệt đối.
a) Giá trị gần đúng của $1,02^5$ là:
$$1^5+5.1^4 \cdot 0,02=1,1$$
b) $1,02^5=1,104$
Sai số tuyệt đối là: $1,104-1,1=0,004$
Bài tập 8.16 trang 75
a) Viết công thức tính số dân của tỉnh đó sau 1 năm, sau 2 năm. Từ đó suy ra công thức tính số dân của tỉnh đó sau 5 năm nữa là $P=800\left(1+\frac{r}{100}\right)^{5}$ (nghìn người).
b) Với $r=1,5\%$, dùng hai số hạng đầu trong khai triển của $(1+0,015)^{5}$, hãy ước tính số dân của tỉnh đó sau 5 năm nữa (theo đơn vị nghìn người).
Áp dụng công thức khai triển:
$$(a+b)^5=a^5+5 a^4 b+10 a^3 b^2+10 a^2 b^3+5 a b^4+b^5$$
a) Để tính số dân năm sau, ta lấy số dân năm trước cộng với số dân tăng hằng năm (Số dân tăng hằng năm là $r\%$ của số dân năm trước).
Số dân của tỉnh đó sau 1 năm là:
$P_1=800+800 . r \% \\\\ =800(1+r \%) \\\\ =800\left(1+\frac{r}{100}\right)^1$ (nghìn người).
Số dân của tỉnh đó sau 2 năm là:
P_2=P_1+P_1.r\%\\\\=800\left(1+\frac{r}{100}\right)^1+800\left(1+\frac{r}{100}\right)^1 \cdot \frac{r}{100} \\\\ =800\left(1+\frac{r}{100}\right)^1\left(1+\frac{r}{100}\right) \\\\ =800\left(1+\frac{r}{100}\right)^2
Do đó, công thức tính số dân của tỉnh đó sau 5 năm nữa là:
$P_5=800\left(1+\frac{r}{100}\right)^5$ (nghìn người).
b) Với $r=1,5$, suy ra $\frac{r}{100}=\frac{1,5}{100}=0,015$.
Ta có khai triển:
$$(1+0,015)^5=1^5+5 \cdot 1^4.0,015+10.1^3.(0,015)^2+10.1^2.(0,015)^3+5.1.(0,015)^4+(0,015)^5 .$$
Do đó:
$(1+0,015)^5 \approx 1^5+5.1^4.0,015=1,075$.
Số dân của tỉnh đó sau 5 năm nữa là:
$$P_5=800.(1+0,015)^5 \approx 800.1,075=860 \text { (nghìn người) }$$
Vậy số dân của tỉnh đó sau 5 năm nữa xấp xỉ khoảng 860 nghìn người.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Nhị thức Newton Chương Đại số tổng hợp Toán 10 Kết nối tri thức tập 2 ở các trang 72, 73, 74, 75. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!





