Giải SGK bài 1 Hàm số bậc 2 Toán 10 Kết nối tri thức Tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Hàm số bậc 2. Đây là bài học thuộc bài 16 chương VI trang 11, 12, 13, 14, 15, 16, 17, 18 sách Toán 10 Kết nối tri thức tập 2. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi trong SGK của bài 16
Dưới đây là phương pháp và bài giải chi tiết cho câu hỏi mở đầu, các hoạt động cùng phần luyện tập ở các trang 11, 12, 13, 14, 15 trong bài Hàm số bậc 2. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Câu hỏi mở đầu trang 11
Hỏi hai cột góc hàng rào cần phải cắm cách bờ tường bao xa để mảnh đất được rào chắn của bác có diện tích lớn nhất?
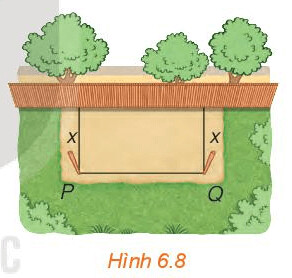
Sau bài học này, ta giải quyết được bài toán trên như sau:
Gọi $x($ mét, $x>0)$ là khoảng cách từ điểm cọc $\mathrm{P}$ và $\mathrm{Q}$ đến bờ tường.
Tấm lưới dài 20 m và được rào chắn ba mặt áp lên bờ tường như Hình 6.8, do đó ta có:
$$x+x+P Q=20$$
Suy ra: $P Q=20-x-x=20-2 x(m)$.
Vì $P Q \gt 0$ (độ dài dương) nên $20-2 x \gt0 \Leftrightarrow 2 x \lt 20 \Leftrightarrow x \lt10$.
Do đó ta có điều kiện của $x$ là $0 \lt x \lt 10$.
Mảnh đất được rào chắn có dạng hình chữ nhật với hai kích thước là $x(m)$ và $20-2x(m)$ với $0 \lt x \lt 10$.
Khi đó diện tích của mảnh đất là $S(x)=x\cdot(20-2 x)=-2 x^2+20 x$.
Theo yêu cầu bài toán, ta cần tìm giá trị của $x$ để $S(x)$ có giá trị lớn nhất.
Ta có:
$S(x)=-2\left(x^2-10 x\right)=-2\left(x^2-2 \cdot 5 \cdot x+25\right)+50=-2(x-5)^2+50 \leq 50$ với mọi số thực $x$.
Dấu “=” xảy ra khi $x -5=0 \Leftrightarrow x=5$ (thỏa mãn điều kiện $0 \lt x \lt 10$ ).
Do đó giá trị lớn nhất của $S(x)$ là 50 tại $x=5$.
Vậy hai cột góc hàng rào cần phải cắm cách bờ tường 5m để mảnh đất được rào chắn của bác Việt có diện tích lớn nhất.
Hoạt động 1 trang 11
a) Độ dài cạnh PQ của mảnh đất.
b) Diện tích S(x) của mảnh đất được rào chắn.

a) Theo bài ra ta có: $x+x+P Q=20 \Rightarrow P Q=20-2 x(\mathrm{~m})$
b) Diện tích của mảnh đất được rào chắn là:
$x . P Q=x \cdot(20-2 x)=-2 x^2+20 x\left(m^2\right)$
Câu hỏi trang 12
A. $y=x^4+3 x^2+2$
B. $y=\frac{1}{x^2}$
C. $y=-3 x^2+1$
D. $y=3\left(\frac{1}{x}\right)^2+3 \cdot \frac{1}{x}-1$
Hàm số bậc hai là hàm số có dạng: $y=a x^2+b x+c(a \neq 0)$
Đáp án đúng là: C
Hàm số bậc hai là hàm số cho bởi công thức $y=a x^2+b x+x$ với $a, b, c$ là các hằng số và $\mathrm{a} \neq 0$.
Vậy trong các hàm số đã cho thì hàm số $\mathrm{y}=-3 \mathrm{x}^2+1$ là hàm số bậc hai với các hệ số $a=-3, b=0$ và $c=1$.
Chú ý: Hàm số $y=3\left(\frac{1}{x}\right)^2+3 \frac{1}{x}-1$ không phải là hàm số bậc hai, mà đây là hàm số có thể đưa về dạng bậc hai nếu ta đặt $t=\frac{1}{x}$.
Luyện tập 1 trang 12
a) Hàm số đã cho có phải hàm số bậc hai không? Nếu có, hãy xác định các hệ số a, b, c của nó.
b) Thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá trị sau của hàm số đã cho

Hàm số có dạng $a x^2+b x+c(a \neq 0)$ là hàm số bậc hai
a) Ta có
$(x-1)(2-3 x)=2 x-3 x^2-2+3 x=-3 x^2+5 x -2$
Do đó hàm $\mathrm{y}=(\mathrm{x}-1)(2-3 \mathrm{x})$ là hàm số bậc hai với $a=-3 ; b=5 ; c=-2$

Vận dụng 1 trang 12
$h=19,6-4,9 t^2 ; h, t \geq 0$.
a) Hỏi sau bao nhiêu giây kể từ khi rơi viên bi chạm đất?
b) Tìm tập xác định và tập giá trị của hàm số h.
a) Để viên bi chạm đất thì $h=0 \Leftrightarrow 19,6-4,9 t^2=0$ $\Leftrightarrow 4,9 t^2=19,6 \Leftrightarrow t^2=4$
Do $t \geq 0$ nên $\mathrm{t}=2$ (s)
Vậy sau 2 giây thì viên bi chạm đất
b) Theo bài ra ta có: $t \geq 0$ nên tập xác định của hàm số h là $D=[0 ;+\infty)$
Mặt khác: $4,9 t^2 \geq 0 \Rightarrow 19,6-4,9 t^2 \leq 19,6$
$\Rightarrow 0 \leq h \leq 19,6$. Do đó tập giá trị của hàm số h là $[0 ; 19,6]$
Hoạt động 2 trang 12
a) Trên mặt phẳng toạ độ $O x y$, biểu diễn toạ độ các điểm trong bảng giá trị của hàm số lập được ở Ví dụ 1. Nối các điểm đã vẽ lại ta được dạng đồ thị hàm số $y=-2 x^{2}+20 x$ trên khoảng $(0 ; 10)$ như trong Hình 6.10. Dạng đồ thị của hàm số $y=-2 x^{2}+20 x$ có giống với đồ thị của hàm số $y=-2 x^{2}$ hay không?
c) Thực hiện phép biến đổi
y=-2 x^{2}+20x \\\\ =-2\left(x^{2}-10 x\right) \\\\ =-2\left(x^{2}-2 . 5 . x+25\right)+50 \\ =-2(x-5)^{2}+50
Hãy cho biết giá trị lớn nhất của diện tích mảnh đất được rào chắn. Từ đó suy ra lời giải của bài toán ở phần mở đầu.
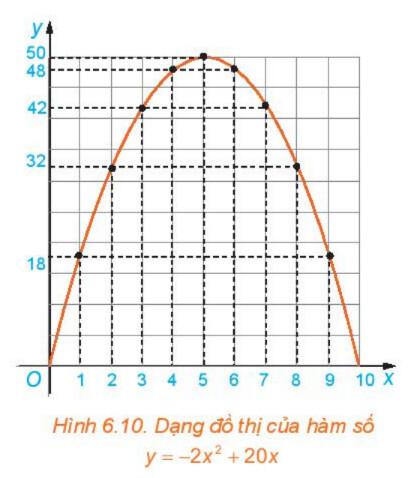
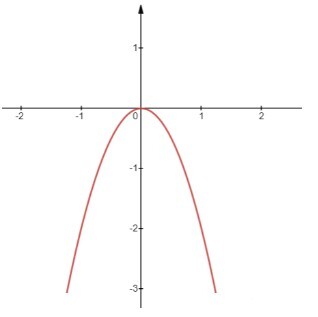
Nhìn vào 2 đồ thị, ta thấy dạng đồ thị của hàm số $y=-2 x^2+20 x$ giống với dạng đồ thị $y=-2 x^2$
b) Tọa độ điểm cao nhất là $(5 ; 50)$
c) Ta có:
S(x)=y=-2 x^2+20x \\\\ =-2\left(x^2-10 x\right) \\\\ =-2\left(x^2-2.5 . x+25\right) +50 \\ =-2(x-5)^2+50 (x-5)^2 \geq 0 \\\\ \Rightarrow-2(x-5)^2+50 \leq 50 \\\\ \Rightarrow S(x) \leq 50
Do đó diện tích lớn nhất của mảnh đất rào chắn là $50\left(m^2\right)$ khi $x=5$
Hoạt động 3 trang 13
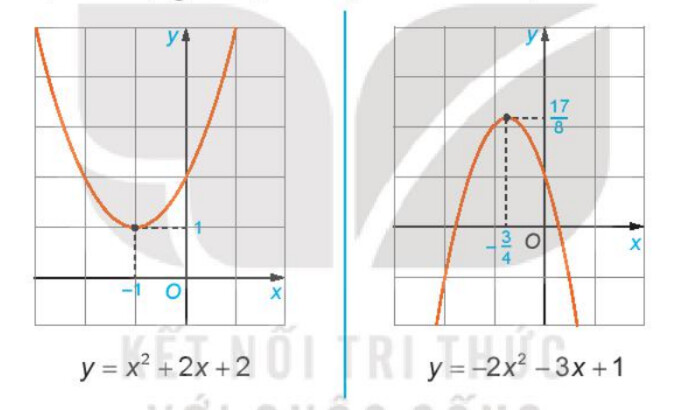
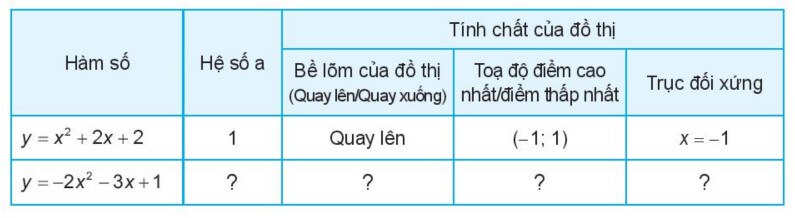
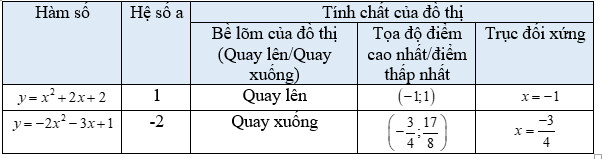
Quan sát đồ thị hàm số $y=-2 x^2-3 x+1$ ta thấy:
+ Hệ số a của hàm số là $\mathrm{a}=-2$;
+ Bề Iõm của đồ thị quay xuống;
+ Đồ thị có điểm cao nhất và điểm này có tọa độ $\left(-\frac{3}{4} ; \frac{17}{8}\right)$;
$+$ Trục đối xứng $x=-\frac{3}{4}$.
Luyện tập 2 trang 15
-Vẽ đồ thị $y=a x^2+b x+c(a \neq 0)$
Là 1 parabol có đỉnh là điểm $I\left(-\frac{b}{2 a} ;-\frac{\Delta}{4 a}\right)$, có trục đối xứng là đường thẳng $x=-\frac{b}{2 a}$
Quay bề lõm lên trên nếu $a>0$, quay bề lõm xuống dưới nếu $a<0$
Xác định 1 vài điểm đặc biệt đồ thị đi qua
– Quan sát đồ thị hàm số trên (a;b)
Hàm số đồng biến nếu đồ thị có dạng đi lên từ trái sang phải.
Hàm số nghịch biến nếu đồ thị có dạng đi xuống từ trái sang phải
– Giá trị nhỏ nhất của hàm số là điểm có vị trí thấp nhất trên đồ thị.
Vẽ đồ thị $y=3 x^2-10 x+7$
– Có đỉnh $I\left(\frac{5}{3} ;-\frac{4}{3}\right)$, có trục đối xứng là đường thẳng $x=\frac{5}{3}$
– Đi qua điểm $(0 ; 7) ;(1 ; 0)$
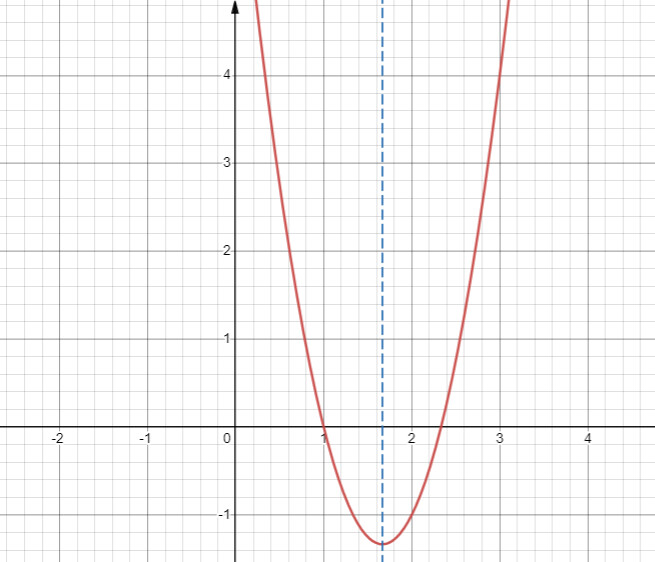
– Giá trị nhỏ nhất của hàm số là tại điểm có tọa độ $\left(\frac{5}{3} ;-\frac{4}{3}\right)$
Vận dụng 2 trang 15
Hãy giúp bạn Nam ước lượng độ cao của đỉnh trụ tháp cầu (so với mặt đất).

Chọn hệ trục tọa độ Oxy sao cho một chân trụ tháp đặt tại gốc tọa độ, chân còn lại đặt trên tia $\mathrm{Ox}$. Khi đó trụ tháp là một phần của đồ thị hàm số dạng $y=a x^2+b x$
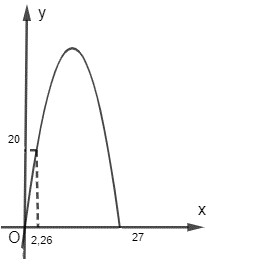
Đồ thị $y=a x^2+b x$ đi qua điểm có tọa độ $(2,26 ; 20)$ và $(27 ; 0)$
Nên ta có \begin{cases} a. (2,26)^2 +b.2,26=20 \\ a.27^2 +b.27=0 \\ \end{cases} \Longleftrightarrow \begin{cases} a \approx -0,358 \\ b \approx 9,666 \\\end{cases}
Do đó ta có hàm số $y=-0,358 x^2+9,666 x$
Tọa độ đỉnh là $x=\frac{-b}{2 a}=13,5 ; y=65,2455$
Vậy độ cao của đỉnh trụ tháp cầu so với mặt đất khoảng $65,2455m$
Giải bài tập vận dụng trang 11 SGK Toán 10 bài 16
Phần tiếp theo sẽ cung cấp cho các bạn phương pháp cùng lời giải trong phần bài tập trang 16 cực kỳ dễ hiểu và chi tiết. Cùng HocThatGioi rèn luyện và nâng cao kỹ năng giải quyết các vấn đề thực tế thông qua các phương pháp, công thức toán học từ bài Hàm số bậc 2 ở trên.
Bài tập 6.7 trang 16
a) $y=x^2-3 x+2$
b) $y=-2 x^2+2 x+3$
c) $y=x^2+2 x+1$
d) $y=-x^2+x-1$
Vẽ đồ thị $y=a x^2+b x+c(a \neq 0)$
Là 1 parabol có đỉnh là điểm $I\left(-\frac{b}{2 a} ;-\frac{\Delta}{4 a}\right)$, có trục đối xứng là đường thẳng $x=-\frac{b}{2 a}$ Quay bề lõm lên trên nếu $\mathrm{a}>0$, quay bề lõm xuống dưới nếu $\mathrm{a}<0$
Xác định các điểm (đặc biệt) thuộc đồ thị.
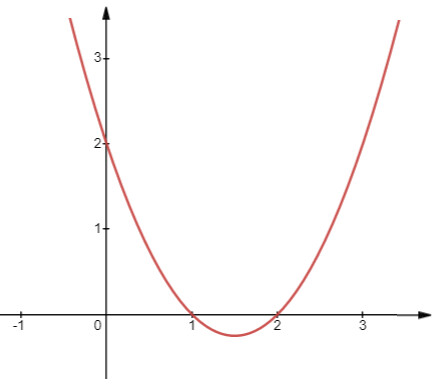
a) Đồ thị $y=x^2-3 x+2$
– Có đỉnh là điểm $I\left(\frac{3}{2} ;-\frac{1}{4}\right)$, có trục đối xứng là đường thẳng $x=\frac{3}{2}$
– $a=1>0$, quay bề lõm lên trên
– Đi qua điểm (0;2);(1;0)
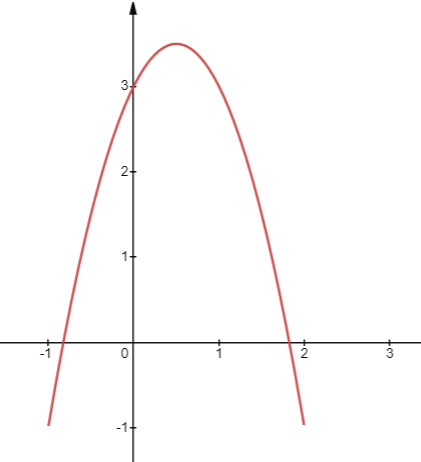
– Có đỉnh là điểm $I\left(\frac{1}{2} ; \frac{7}{2}\right)$, có trục đối xứng là đường thẳng $x=\frac{1}{2}$ – $a=-2<0$, quay bề lõm xuống dưới
– Đi qua điểm $(0 ; 3) ;(1 ; 3)$
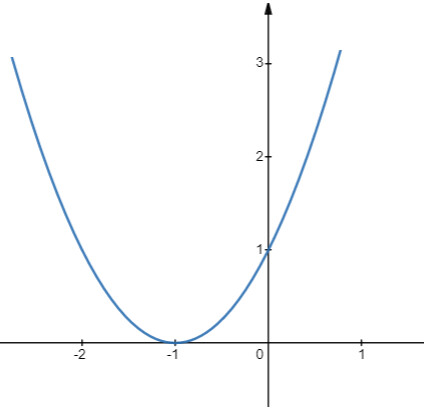
– Có đỉnh là điểm $I(-1 ; 0)$, có trục đối xứng là đường thẳng $x=-1$ – $a=1>0$, quay bề lõm lên trên
– Đi qua điểm (0;1); (1;4)
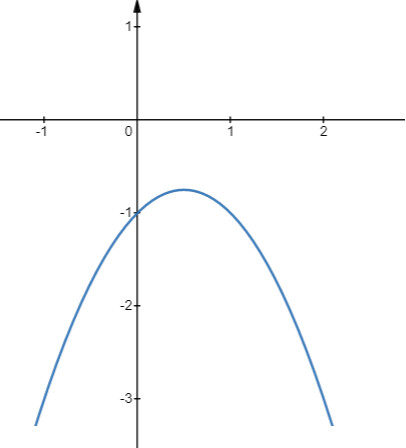
– Có đỉnh là điểm $I\left(\frac{1}{2} ; \frac{-3}{4}\right)$, có trục đối xứng là đường thẳng $x=\frac{1}{2}$ – $a=-1<0$, quay bề lõm xuống dưới
Bài tập 6.8 trang 16
Quan sát đồ thị hàm số trên $(a ; b)$
Hàm số đồng biến nếu đồ thị có dạng đi lên từ trái sang phải.
Hàm số nghịch biến nếu đồ thị có dạng đi xuống từ trái sang phải
a) Hàm số $y=x^2-3 x+2$ nghịch biến trên khoảng $\left(-\infty ; \frac{3}{2}\right)$; đồng biến trên khoảng $\left(\frac{3}{2} ;+\infty\right)$
b) Hàm số $y=-2 x^2+2 x+3$ đồng biến trên khoảng $\left(-\infty ; \frac{1}{2}\right)$; nghịch biến trên khoảng $\left(\frac{1}{2} ;+\infty\right)$
c) Hàm số $y=x^2+2 x+1$ nghịch biến trên khoảng $(-\infty ;-1)$; đồng biến trên khoảng $(-1 ;+\infty)$
d) Hàm só $y=-x^2+x-1$ đồng biến trên khoảng $\left(-\infty ; \frac{1}{2}\right)$; nghịch biến trên khoảng $\left(\frac{1}{2} ;+\infty\right)$
Bài tập 6.9 trang 16
a) Đi qua 2 điểm $\mathrm{A}(1 ; 0)$ và $\mathrm{B}(2 ; 4)$
b) Đi qua điểm $\mathrm{A}(1 ; 0)$ và có trục đối xứng $x=1$
c) Có đỉnh $I(1 ; 2)$
d) Đi qua điểm $C(-1 ; 1)$ và có tung độ đỉnh $-0,25$
Đồ thị hàm số $y=a x^2+b x+c$ có:
– Đỉnh là điểm $I\left(\frac{-b}{2 a} ; \frac{-\Delta}{4 a}\right)$
– Trục đối xứng là đường thẳng $x=\frac{-b}{2 a}$
a) Đồ thị hàm số $y=a x^2+b x+1$ đi qua điểm $\mathrm{A}(1 ; 0)$ nên:
$a .1^2+b .1+1=0 \Leftrightarrow a+b=-1$
Đồ thị hàm số $y=a x^2+b x+1$ đi qua điểm $\mathrm{B}(2 ; 4)$ nên:
$$a .2^2+2 b+1=4 \Leftrightarrow 4 a+2 b=3$$
Từ 2 phương trình trên, ta có $a=\frac{5}{2} ; b=\frac{-7}{2}$
=> Hàm số cần tìm là $y=\frac{5}{2} x^2-\frac{7}{2} x+1$
b) Đồ thị hàm số $y=a x^2+b x+1$ đi qua điểm $\mathrm{A}(1 ; 0)$ nên:
$a .1^2+b .1+1=0 \Leftrightarrow a+b=-1$
Đồ thị hàm số $y=a x^2+b x+1$ có trục đối xứng $\mathrm{x}=1$
$$\frac{-b}{2 a}=1 \Leftrightarrow-b=2 a \Leftrightarrow 2 a+b=0$$
Từ 2 phương trình trên, ta có $a=1 ; b=-2$
$=>$ Hàm số cần tìm là $y=x^2-2 x+1$
c) Đồ thị hàm số $y=a x^2+b x+1$ có đỉnh $I(1 ; 2)$ nên:
$$\begin{aligned}& \frac{-b}{2 a}=1 \Leftrightarrow-b=2 a \Leftrightarrow 2 a+b=0 \\& a .1^2+b .1+1=2 \Leftrightarrow a+b=1\end{aligned}$$
Từ 2 phương trình trên, ta có $a=-1 ; b=2$
$=>$ Hàm số cần tìm là $y=-x^2+2 x+1$
d) Đồ thị hàm số $y=a x^2+b x+1$ đi qua điểm $C(-1 ; 1)$ nên:
$a \cdot(-1)^2+b \cdot(-1)+1=1 \Leftrightarrow a-b=0 \Leftrightarrow a=b$
Đồ thị hàm số $y=a x^2+b x+1$ có tung độ đỉnh là $-0,25$ nên:
$$\frac{-\Delta}{4 a}=-0,25 \Leftrightarrow-\frac{b^2-4 . a .1}{4 a}=-0,25 \Leftrightarrow b^2-4 a=a \Leftrightarrow b^2=5 a$$
Thay $a=b$ ta có:
$b^2=5 b \Leftrightarrow b=0$ hoặc $b=5$
Vì $a \neq 0$ nên $a=b=5$
$=>$ Hàm số cần tìm là $y=5 x^2+5 x+1$
Bài tập 6.10 trang 16
Đồ thị hàm số $y=a x^2+b x+c$ có đỉnh là $I\left(\frac{-b}{2 a} ; \frac{-\Delta}{4 a}\right)=>$ tìm a,b,c.
Đồ thị hàm số $y=a x^2+b x+c$ đi qua điểm $\mathrm{A}(8 ; 0)$ nên:
$$a .8^2+b .8+c=0 \Leftrightarrow 64 a+8 b+c=0$$
Đồ thị hàm số $y=a x^2+b x+c$ có đỉnh là l(6;-12):
$$\begin{aligned}& \frac{-b}{2 a}=6 \Leftrightarrow-b=12 a \Leftrightarrow 12 a+b=0 \\& a .6^2+6 b+c=-12 \Leftrightarrow 36 a+6 b+c=-12\end{aligned}$$
Từ 3 phương trình trên ta có: $a=3 ; b=-36, c=96$
$=>$ Hàm số cần tìm là $y=3 x^2-36 x+96$
Bài tập 6.11 trang 16
a) $(\mathrm{P})$ nằm hoàn toàn trên trục hoành
b) $(\mathrm{P})$ nằm hoàn toàn dưới trục hoành
c) (P) cắt trục hoành tại hai điểm phân biệt và có đỉnh nằm phía dưới trục hoành
d) (P) tiếp xúc với trục hoành và nằm phía trên trục hoành
a) $(P)$ nằm hoàn toàn trên trục hoành thì $(P)$ không cắt trục hoành
=> Phương trình $a x^2+b x+c=0$ vô nghiệm $=>\Delta\lt0$
$(\mathrm{P})$ nằm hoàn toàn trên trục hoành thì bề lõm phải hướng lên trên $=>\mathrm{a}\gt0$
b) Tương tự câu a:
$(\mathrm{P})$ nằm hoàn toàn dưới trục hoành thì $(\mathrm{P})$ không cắt trục hoành
$=>$ Phương trình $a x^2+b x+c=0$ vô nghiệm $=>$ $\Delta\lt0$
( $P$ ) nằm hoàn toàn dưới trục hoành thì bề lõm phải hướng xuống dưới $=>\mathrm{a}\gt0$
c) ( $\mathrm{P})$ cắt trục hoành tại hai điểm phân biệt
$=>$ Phương trình $a x^2+b x+c=0$ có 2 nghiệm phân biệt=> $\Delta\gt0$
(P) có đỉnh nằm phía dưới trục hoành mà có 2 nghiệm phân biệt thì bề lõm phải hướng lên trên => $a\gt0$
d) $(\mathrm{P})$ tiếp xúc với trục hoành
$=>$ Phương trình $a x^2+b x+c=0$ có duy nhất 1 nghiệm $=>\Delta=0$
$(\mathrm{P})$ nằm phía trên trục hoành nên bề lõm phải hướng lên trên $=>a\gt0$
Bài tập 6.12 trang 16
An nói: Tớ đọc ở một tài liệu thấy nói rằng cổng Trường Đại học Bách khoa Hà Nội (H.6.14) có dạng một parabol, khoảng cách giữa hai chân cổng là $8 \mathrm{~m}$ và chiều cao của cổng tính từ một điểm trên mặt đất cách chân cổng $0,5 \mathrm{~m}$ là $2,93 \mathrm{~m}$. Từ đó tó́ tính ra được chiểu cao của cổng parabol đó là $12 \mathrm{~m}$.
Sau một hồi suy nghĩ, Bình nói: Nếu dữ kiện như bạn nói, thì chiều cao của cổng parabol mà bạn tính ra ở trên là không chính xác.
Dựa vào thông tin mà An đọc được, em hãy tính chiều cao của cổng Trường Đại học Bách khoa Hà Nội để xem kết quả bạn An tính được có chính xác không nhé!

Chọn hệ trục tọa độ $\mathrm{Oxy}$ như hình vẽ với $\mathrm{Oy}$ là trục đối xứng của cổng parabol:
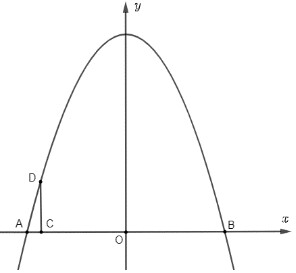
Theo bài ra ta có:
$\mathrm{AB}=8 \mathrm{~m} \Rightarrow \mathrm{AO}=\mathrm{OB}=4 \mathrm{~m}$
$\mathrm{AC}=0,5 \mathrm{~m}=>\mathrm{OC}=\mathrm{OA}-\mathrm{AC}=3,5 \mathrm{~m}$
=> Parabol đi qua điểm $A(-4 ; 0) ; B(4 ; 0) ; C(-3,5 ; 2,93)$
Do đó ta có các phương trình sau:
a. $(-4)^2+b(-4)+c=0 \Leftrightarrow 16 a-4 b+c=0$
$a .4^2+4 b+c=0 \Leftrightarrow 16 a+4 b+c=0$
a. $(-3,5)^2+b(-3,5)+c=2,93 \Leftrightarrow 12,25 a-3,5 b+c=2,93$
Từ 3 phương trình trên, ta có: $a=\frac{-293}{375} ; b=0 ; c=\frac{4688}{375}$
Tọa độ đỉnh là $I\left(0 ; \frac{4688}{375}\right)$
Vậy chiều cao của cổng parabol là $\frac{4688}{375} \approx 12,5 m$
=> Kết quả của An tính ra không chính xác
Bài tập 6.13 trang 16
a) Tính diện tích mảnh vườn hình chữ nhật rào được theo chiều rộng x (mét) của nó.
b) Tìm kích thước của mảnh vườn hình chữ nhật có diện tích lớn nhất mà bác Hùng có thể rào được.
Theo bài ra ta có chu vi của mảnh vườn hình chữ nhật bằng $40 \mathrm{~m}$
Tính được chiều dài của mảnh vườn => diện tích mảnh vườn
a) Gọi chiều dài mảnh vườn là $a(m)$
Khi đó ta có $2 a+2 x=40 \Leftrightarrow a=20-x$
Vậy diện tích mảnh vườn hình chữ nhật là: $S=a . x=(20-x) x=-x^2+20 x$
b) Để diện tích mảnh vườn lớn nhất thì S phải lớn nhất:
Ta có $S=-x^2+20 x=-\left(x^2-20 x+100\right)+100=100-(x-10)^2 \leq 100$ (vì $(x-10)^2 \geq 0$ )
Diện tích mảnh vườn lớn nhất là $100\left(m^2\right)$ khi $x=10$
Bài tập 6.14 trang 16
a) Tím độ cao cực đại của vật trong quá trình bay
b) Tính khoảng cách từ điểm chạm mặt đất sau khi bay của vật đến gốc O. Khoảng cách này gọi là tầm xa của quỹ đạo.
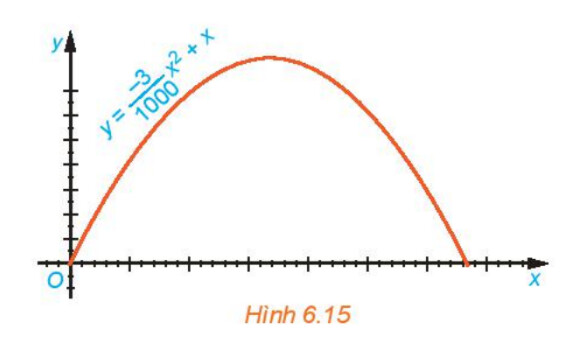
a) Độ cao cực đại của vật là tung độ đỉnh của hàm số $y=\frac{-3}{1000} x^2+x$
b) Khoảng cách từ điểm chạm mặt đất sau khi bay của vật đến gốc $\mathrm{O}$ là hoành độ của điểm khác gốc tọa độ làm cho y=0
a) Tung độ đỉnh của hàm số $y=\frac{-3}{1000} x^2+x$ là:
$$\frac{-\Delta}{4 a}=\frac{-\left(1^2-4 \cdot \frac{-3}{1000} \cdot 0\right)}{4 \cdot \frac{-3}{1000}}=\frac{250}{3}$$
Vậy độ cao cực đại của vật là $\frac{250}{3}(m)$
b) Vật chạm đất khi:
$y=0 \Leftrightarrow \frac{-3}{1000} x^2+x=0 \Leftrightarrow x=\frac{1000}{3}$ và $\mathrm{x}=0$ (loại)
Vậy khoảng cách từ điểm chạm mặt đất sau khi bay của vật đến gốc O là $\frac{1000}{3}(\mathrm{~m})$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Hàm số bậc 2 Chương Hàm số, đồ thị và ứng dụng Toán 10 Kết nối tri thức tập 2 ở các trang 11, 12, 13, 14, 15, 16, 17, 18. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!





