Giải SGK bài 15 Hàm số trang 4, 5, 6, 7, 8, 9, 10 Toán 10 Kết nối tri thức Tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Hàm số. Đây là bài học thuộc bài 15 chương VI trang 4, 5, 6, 7, 8, 9, 10 sách Toán 10 Kết nối tri thức tập 2. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi trong SGK của bài 15
Cùng HocThatGioi đi tìm phương pháp và bài giải chi tiết cho câu hỏi mở đầu, các hoạt động cùng phần luyện tập ở các trang 4, 5, 6, 7, 8, 9 trong bài Hàm số ngay dưới đây nhé!
Câu hỏi mở đầu trang 4
Có cách nào mô tả sự phụ thuộc của số tiền phải trả vào tổng lượng điện tiêu thụ hay không?
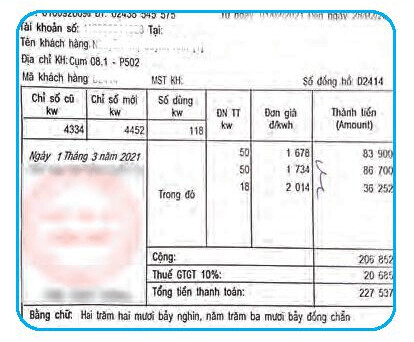
Quan sát hóa đơn ta thấy:
Tổng lượng điện tiêu thụ trong tháng là: $50 + 50 + 18 = 118 (kW)$.
Số tiền phải trả (chưa tính thuế giá trị gia tăng) là 206 852 đồng.
Giá tiền điện được tính theo bậc thang cho từng số lượng điện đã dùng, cụ thể:
Dùng 50 kW đầu thì đơn giá là 1678 đồng/ 1 kW.
Dùng 50 kW tiếp theo thì đơn giá là 1734 đồng/ 1 kW.
Dùng 100 kW tiếp thì đơn giá là 2014 đồng/ 1 kW.
Ở hóa đơn điện trên kia, người sử dụng điện dùng 118 kW, có nghĩa phải trả theo 3 bậc.
Nên ta tính số tiền điện bằng cách thực hiện phép tính:
$50 . 1678 + 50 . 1734 + 18 . 2014 = 206 852 (đồng)$
Vậy ta mô tả được sự phụ thuộc của số tiền điện phải trả vào tổng lượng điện tiêu thụ như trên.
Hoạt động 1 trang 5

b) Trong Bảng $6.1$, mỗi thời điểm tương ứng với bao nhiêu giá trị của nồng độ bụi PM 2.5?
a) Dựa vào Bảng 6.1, ta thấy:
– Tại thời điểm 8 giờ, nồng độ bụi PM 2.5 là $57,9$
– Tại thời điểm 12 giờ, nồng độ bụi PM 2.5 là $69,07$
– Tại thời điểm 16 giờ, nồng độ bụi PM 2.5 là $81,78$
b) Trong Bảng 6.1, mỗi thời điểm tương ứng với 1 giá trị của nồng độ bụi PM $2.5$
Ví dụ: tại 0 giờ, nồng độ bụi PM 2.5 là $74,27$
Hoạt động 2 trang 5
b) Trong khoảng thời gian đó, năm nào mực nước biển trung bình tại Trường Sa cao nhất, thấp nhất?
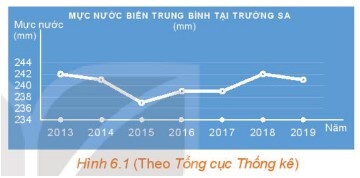
a) Quan sát biểu đồ trên, ta biết được thời gian theo dõi mực nước biển ở Trường Sa được thể hiện từ năm 2013 đến năm 2019
b) Trong khoảng thời gian đó:
– Năm 2013, 2019 là năm có mực nước cao nhất
– Năm 2015 là năm có mực nước thấp nhất
Hoạt động 3 trang 5
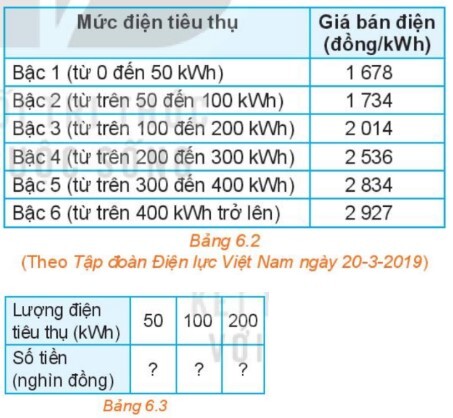
Dựa vào Bảng 6.2, ta xem xét lượng điện tiêu thụ nằm ở bậc nào, từ đó ta tính được số tiền và công thức mô tả.
a) Số tiền phải trả tương ứng với lượng điện $50 \mathrm{kWh}$ là:
$50.1,678=83,9$ (nghìn đồng)
Số tiền phải trả tương ứng với lượng điện $100 \mathrm{kWh}$ là:
$50.1,678+(100-50) .1,734=170,6$ (nghìn đồng)
Số tiền phải trả tương ứng với lượng điện $200 \mathrm{kWh}$ là:
$50.1,678+(100-50) .1,734+(200-100) .2,014=372$ (nghìn đồng)
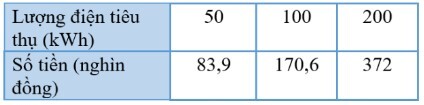
$$y=1,678 . x$$
Luyện tập 1 trang 6

c) Cho hàm số $y=f(x)=-2 x^2$. Tính $\mathrm{f}(1); f(2)$ và tìm tập xác định, tập giá trị của hàm số này.
Tập xác định là tập D với mỗi giá trị của x sẽ thuộc tập D
Tập tất cả giá trị y nhận được là tập giá trị của hàm số
a) Mỗi giá trị của x tương ứng sẽ có 1 giá trị của y nên Bảng $6.4$ cho ta một hàm số.
Tập xác định của hàm số $D=\{2013 ; 2014 ; 2015 ; 2016 ; 2017 ; 2018\}$
Tập giá trị của hàm số $\{73,1 ; 73,2 ; 73,3 ; 73,4 ; 73,5\}$
b) Giá trị của hàm số tại $x=2018$ là $242$
Tập xác định của hàm số $D=(2013 ; 2019)$
Tập giá trị của hàm số $(236 ; 242)$
$$\begin{array}{r}f(1)=-2.1^2=-2 \\f(2)=-2.2^2=-8\end{array}$$
Tập xác định của hàm số $y=f(x)=-2 x^2$ là $\mathbb{R}$
Ta có $x^2 \geq 0 \Rightarrow-2 x^2 \leq 0$, do đó $y \leq 0$
Tập giá trị của hàm số $y=f(x)=-2 x^2$ là $(-\infty ; 0)$
Hoạt động 4 trang 7
$$(0 ; 0),(2 ; 2),(-2 ; 2),(1 ; 2),(-1 ; 2) .$$
Nêu nhận xét về mối quan hệ giữa hoành độ và tung độ của những điểm nằm trên đồ thị.
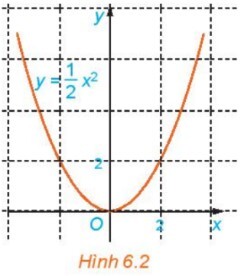
Dựa vào độ thị ta thấy $(0 ; 0) ;(2 ; 2) ;(-2 ; 2)$ nằm trên đồ thị hàm số $y=\frac{1}{2} x^2$
Với hoành độ x = 2 thì $$y=\frac{1}{2} \cdot 0^2=0$$
Với x = 2 thì $y=\frac{1}{2} \cdot 2^2=2$
Với x = -2 thì $$y=\frac{1}{2} \cdot(-2)^2=2$$
Vậy hoành độ và tung độ của những điểm nằm trên đồ thị thỏa mãn hàm số $y=\frac{1}{2} x^2$.
Luyện tập 2 trang 7
b) Vẽ đồ thị của các hàm số $y=2 x+1$ và $y=2 x^2$ trên cùng một mặt phẳng tọa độ.
a) Để $y=8 \Leftrightarrow \frac{1}{2} x^2=8 \Leftrightarrow x^2=16 \Leftrightarrow x=4$ hoăc $x=-4$
b) Vẽ đồ thị $y=2 x+1$ :
-Là đồ thị bậc nhất nên đồ thị là đường thẳng đi qua điểm có tọa độ $(0 ; 1)$ và $$(-1 ;-1)$$
Vẽ đồ thị $y=2 x^2$
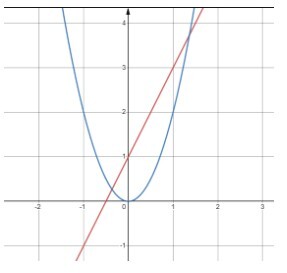
Vận dụng 1 trang 7
Theo bảng giá bán lẻ điện sinh hoạt (Bảng 6.2) thì số tiền phải trả là:
$y=1,678 \cdot 50+1,734(x-50)=83,9+1,734(x-50)$ hay
$y=1,734 x-2,8$ (nghìn đồng).
Vậy trên tập xác định $D=(50 ; 100]$, hàm số $y$ mô tả số tiền phải thanh toán có công thức là $y=1,734 x-2,8$; tập giá trị của nó là $(83,9 ; 170,6]$.
Hãy vẽ đồ thị ở Hình $6.3$ vào vở rồi vẽ tiếp đồ thị của hàm số $y=1,734 x-2,8$ trên tập $D=(50 ; 100]$.
Với $x = 100$ thì $y = 170,6$ đồ thị của hàm số là đoạn thẳng màu đỏ trên hình sau:
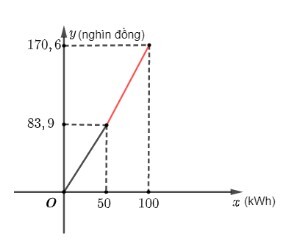
Hoạt động 5 trang 8
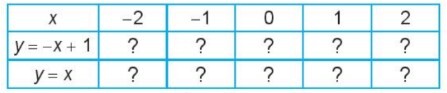
Thay $x$ vào ta có:

Khi $x$ tăng, giá trị $y$ của hàm số $y=-x+1$ giảm
Khi $x$ tăng, giá trị $y$ của hàm số $y=x$ tăng
Hoạt động 6 trang 8
a) Giá trị của $f(x)$ tăng hay giảm khi x tăng trên khoảng $(-\infty ; 0)$ ?
b) Giá trị của $\mathrm{f}(\mathrm{x})$ tăng hay giảm khi $x$ tăng trên khoảng $(0 ;+\infty)$ ?
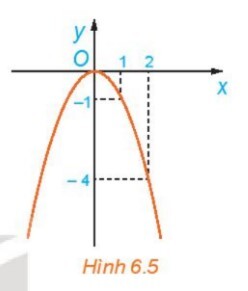
Dựa vào đồ thị, ta thấy:
a) Trên khoảng $(-\infty ; 0)$, giá trị của $f(x)$ tăng
b) Trên khoảng $(0 ;+\infty)$, giá trị của $\mathrm{f}(\mathrm{x})$ giảm
Luyện tập 3 trang 9
a) Hàm số $y=3 x+1$ đồng biến hay nghịch biến trên $\mathbb{R}$
b) Hàm số $y=-2 x^2$ đồng biến hay nghịch biến trên $(-\infty ; 0)$ và $(0 ;+\infty)$
Quan sát đồ thị hàm số trên $(a ; b)$
Hàm số đồng biến nếu đồ thị có dạng đi lên từ trái sang phải.
Hàm số nghịch biến nếu đồ thị có dạng đi xuống từ trái sang phải.
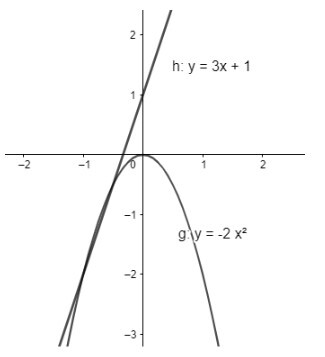
a) Trên $\mathbb{R}$, đồ thị $y=3 x+1$ đi lên từ trái sang phải, như vậy hàm số $y=3 x+1$ đồng biến trên $\mathbb{R}$
b) Trên khoảng $(-\infty ; 0)$, đồ thị $y=-2 x^2$ đi lên từ trái sang phải với mọi $x \in(-\infty ; 0)$, như vậy hàm số đồng biến trên $(-\infty ; 0)$
Trên khoảng $(0 ;+\infty)$, đồ thị $y=-2 x^2$ đi xuống từ trái sang phải với mọi $x \in(0 ;+\infty)$, như vậy hàm số nghịch biến trên $(0 ;+\infty)$
Vận dụng 2 trang 9
a) Tính số tiền phải trả khi di chuyển 25 km.
b) Lập công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển.
c) Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến trên khoảng nào.
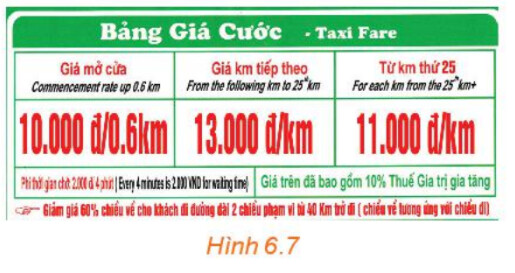
Gọi $x$ là số km taxi đã đi; $y$ (nghìn đồng) là số tiền cước phải trả
a) Khi di chuyển $25 \mathrm{~km}$ thì:
Với 0,6km đầu tiên, số tiền cước phải trả $10000$ (đồng)
Với những km tiếp theo, số tiền cước phải trả $13000.(25-0,6)=317200$ (đồng)
Vậy số tiền cước phải trả $317200+10000=327200$ (đồng)
b) Khi hành khách đi từ $0 \mathrm{~km}$ đến $0,6 \mathrm{~km}$ thì $y=10$ (nghìn đồng)
Khi hành khách đi từ $0,7 \mathrm{~km}$ đến $25 \mathrm{~km}$ thì $y=10+(x-0,6) .13=13 x+2,2$ (nghìn đồng)
Khi khách hàng đi từ $25 \mathrm{~km}$ trở lên $y=13.25+2,2+(x-25) .11=11 x+52,2$ (nghìn đồng)
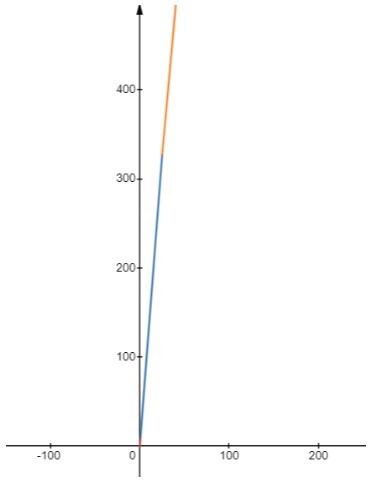
Nhìn trên đồ thị ta có thể thấy đồ thị đồng biến trên $(0 ;+\infty)$.
Giải bài tập vận dụng trang 9 SGK Toán 10 bài 15
Phần tiếp theo sẽ cung cấp cho các bạn phương pháp cùng lời giải trong phần bài tập trang 9 cực kỳ dễ hiểu và chi tiết. Cùng HocThatGioi rèn luyện và nâng cao kỹ năng giải quyết các vấn đề thực tế thông qua các phương pháp, công thức toán học từ bài Hàm số ở trên.
Bài tập 6.1 trang 9
a) $x+y=1$
b) $y=x^2$
c) $y^2=x$
d) $x^2-y^2=0$
Biểu diễn $y$ theo $x$, nếu với mỗi giá trị của $x$ ta chỉ tìm được duy nhất một giá trị $y$ tương ứng thì y là hàm số của $x$.
a) $x+y=1 \Rightarrow y=1-x$, vậy với mỗi giá trị $\mathrm{x}$ chỉ có 1 giá trị y giá trị $\mathrm{y}$, vậy $\mathrm{x}=\mathrm{y}+1$ là hàm số
b) $y=x^2$ là 1 hàm số
c) $y^2=x \Rightarrow y=\sqrt{x}$ hoặc $y=-\sqrt{x}$ (nếu $x \geq 0$ ), vậy 1 giá trị của x lại có 2 giá trị $\mathrm{y}$, nên đây không phải là hàm số
d) $x^2-y^2=0 \Leftrightarrow x^2=y^2, \mathrm{y}=\mathrm{x}$ hoặc $\mathrm{y}=-\mathrm{x}$, vậy 1 giá trị của $\mathrm{x}$ lại có 2 giá trị y, nên đây không phải là hàm số
Bài tập 6.2 trang 9
Ví dụ hàm số y= \frac{\mathrm{-1} }{\mathrm{2} }x
Ta có bảng sau:

Tập xác định của hàm số $D=\left\{-2 ;-1 ;-\frac{1}{2} ; 0 ; \frac{1}{2} ; 1 ; 2\right\}$
Tập giá trị của hàm số $\left\{1 ; \frac{1}{2} ; \frac{1}{4} ; 0 ;-\frac{1}{4} ;-\frac{1}{2} ;-1\right\}$
Bài tập 6.3 trang 9
a) $y=2 x^3+3 x+1$
b) $y=\frac{x-1}{x^2-3 x+2}$
c) $y=\sqrt{x+1}+\sqrt{1-x}$
a) Hàm $y=2 x^3+3 x+1$ là hàm đa thức nên có tập xác định $D=\mathbb{R}$
b) Biểu thức $\frac{x-1}{x^2-3 x+2}$ có nghĩa khi $x^2-3 x+2 \neq 0 \Leftrightarrow x \neq 1$ và $x \neq 2$
Vậy tập xác định của hàm số đã cho là $D=\mathbb{R} /\{1 ; 2\}$
c) Biểu thức $\sqrt{x+1}+\sqrt{1-x}$ có nghĩa khi $x+1 \geq 0$ và $1-x \geq 0$, tức là $-1 \leq x \leq 1$
Vậy tập xác định của hàm số đã cho là $D=[-1 ; 1]$
Bài tập 6.4 trang 9
a) $y=2 x+3$
b) $y=2 x^2$
a) Biểu thức $2 x+3$ có nghĩa với mọi x, nên có tập xác định $D=\mathbb{R}$
Do đó tập giá trị của hàm số là $\mathbb{R}$
b) Biểu thức $2 x^2$ có nghĩa với mọi x, nên có tập xác định $D=\mathbb{R}$
Ta có: $x^2 \geq 0$ Do đó $y=2 x^2 \geq 0$, tập giá trị của hàm số là $[0 ;+\infty)$
Bài tập 6.5 trang 9
а) $y=-2 x+1$
b) $y=-\frac{1}{2} x^2$
Vẽ hình, quan sát đồ thị hàm số trên $(a;b)$
Hàm số đồng biến nếu đồ thị có dạng đi lên từ trái sang phải.
Hàm số nghịch biến nếu đồ thị có dạng đi xuống từ trái sang phải.
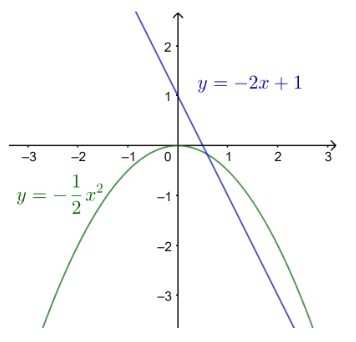
a) Hàm số $y=-2 x+1$ nghịch biến trên $\mathbb{R}$
b) Hàm số $y=-\frac{1}{2} x^2$ đồng biến trên khoảng $(-\infty ; 0)$; nghịch biến trên khoảng $(0 ;+\infty)$
Bài tập 6.6 trang 9
a) Viết công thức của hàm số $T=T(x)$
b) Tính $T(2), T(3), T(5)$ và cho biết ý nghĩa của mỗi giá trị này.
a)
Nếu $02$ thì $T(x)=1,2 \cdot 2+0,9 .(x-2)=0,9 x+0,6$ (triệu đồng)
Số tiền phải trả sau khi thuê x ngày là
T(x)= \begin{cases} 1,2x (0 \lt x \leq 2) \\ 0,9x+0,6(x \gt 2) \end{cases}
b)
$T(2)=1,2.2=2,4$ (triệu đồng)
Ý nghĩa: số tiền khách phải trả khi thuê 2 ngày là 2,4 triệu đồng
$T(3)=0,9.3+0,6=3,3$ (triệu đồng)
Ý nghĩa: số tiền khách phải trả khi thuê 3 ngày là 3,3 triệu đồng
$T(5)=0,9.5+0,6=5,1$
Ý nghĩa: số tiền khách phải trả khi thuê 5 ngày là 5,1 triệu đồng
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Hàm số Chương Hàm số, đồ thị và ứng dụng Toán 10 Kết nối tri thức tập 2 ở các trang 4, 5, 6, 7, 8, 9, 10. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!





