Giải SGK bài 18 chương VI trang 25, 26, 27 Toán 10 Kết nối tri thức tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Phương trình quy về phương trình bậc hai. Đây là bài học thuộc bài 18 chương VI trang 25, 26, 27 sách Toán 10 Kết nối tri thức tập 2. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi trong SGK của bài 18
Dưới đây là phương pháp và bài giải chi tiết cho câu hỏi mở đầu, các hoạt động cùng phần luyện tập ở các trang 25, 26 trong bài Phương trình quy về phương trình bậc hai. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động 1 trang 25
a) Bình phương hai vế của phương trình để khử căn và giải phương trình bậc hai nhận được
b) Thử lại các giá trị x tìm được ở câu a có thỏa mãn phương trình đã cho hay không
a) Bình phương hai vế của phương trình $\sqrt{x^2-3 x+2}=\sqrt{-x^2-2 x+2}$ ta được:
$x^2-3 x+2=-x^2-2 x+2(1)$
Giải phương trình trên ta có:
$$\begin{aligned}& \Leftrightarrow 2 x^2-x=0 \\& \Leftrightarrow x(2 x-1)=0 \\& \Leftrightarrow x=0 \text { hoặc } x=\frac{1}{2}\end{aligned}$$
b) Thử lại ta có:
Với $x=0$, thay vào phương trình đã cho ta được: $\sqrt{0^2-3.0+2}=\sqrt{-0^2-2.0+2} \Leftrightarrow \sqrt{2}=\sqrt{2}$ (luôn đúng)
Với $x=\frac{1}{2}$, thay vào phương trình đã cho ta được:
$\sqrt{\left(\frac{1}{2}\right)^2-3 \cdot \frac{1}{2}+2}=\sqrt{-\left(\frac{1}{2}\right)^2-2 \cdot \frac{1}{2}+2} \Leftrightarrow \sqrt{\frac{3}{4}}=\sqrt{\frac{3}{4}}$ (luôn đúng)
Vậy các giá trị x tìm được ở câu a thỏa mãn phương trình đã cho
Luyện tập 1 trang 25
a) $\sqrt{3 x^2-6 x+1}=\sqrt{-2 x^2-9 x+1}$
b) $\sqrt{2 x^2-3 x-5}=\sqrt{x^2-7}$
Bước 1: Bình phương hai vế và giảii phương trình nhận được
Bước 2: Thử lại các giá trị $x$ nhận được ở trên có thỏa mãn phương trình đã cho hay không $=>$ kết luận nghiệm
a) $\sqrt{3 x^2-6 x+1}=\sqrt{-2 x^2-9 x+1}$
Bình phương hai vế của phương trình $\sqrt{3 x^2-6 x+1}=\sqrt{-2 x^2-9 x+1}$ ta được
$$\begin{aligned}& 3 x^2-6 x+1=-2 x^2-9 x+1 \\& \Leftrightarrow 5 x^2+3 x=0 \\& \Leftrightarrow x(5 x+3)=0 \\& \Leftrightarrow x=0 \text { hoặc } x=\frac{-3}{5}\end{aligned}$$
Thay lần lượt hai giá trị này của $x$ vào phương trình đã cho, ta thấy cả hai giá trị $x=0$; $x=\frac{-3}{5}$ đều thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là $S=\left\{0 ; \frac{-3}{5}\right\}$
b) $\sqrt{2 x^2-3 x-5}=\sqrt{x^2-7}$
Binh phương hai vế của phương trình $\sqrt{2 x^2-3 x-5}=\sqrt{x^2-7}$, ta được:
$$\begin{aligned}& 2 x^2-3 x-5=x^2-7 \\& \Leftrightarrow x^2-3 x+2=0 \\& \Leftrightarrow x=1 \text { hoặc } x=2\end{aligned}$$
Thay lần lượt giá trị của $x$ vào phương trình đã cho, ta thấy không có giá trị nào của $x$ thỏa mãn.
Vậy phương trình đã cho vô nghiệm.
Hoạt động 2 trang 25
a) Bình phương hai vế và giải phương trình nhận được
b) Thử lại các giá trị x tìm được ở câu a có thỏa mãn phương trình đã cho hay không
a) Bình phương hai vế của phương trình $\sqrt{26 x^2-63 x+38}=5 x-6$ ta được:
$$\begin{aligned}& 26 x^2-63 x+38=(5 x-6)^2 \\& \Leftrightarrow 26 x^2-63 x+38=25 x^2-60 x+36 \\& \Leftrightarrow x^2-3 x+2=0 \\& \Leftrightarrow x=1 \text { hoặc } x=2\end{aligned}$$
b) Thử lại:
Với $x=1$ thay vào phương trình đã cho ta được:
$$\begin{aligned}& \sqrt{26.1^2-63.1+38}=5.1-6 \\& \Leftrightarrow 1=-1 \text { (vô lý) }\end{aligned}$$
Với $x=2$ thay vào phương trình đã cho ta được:
$$\begin{aligned}& \sqrt{26.2^2-63.2+38}=5.2-6 \\& \Leftrightarrow \sqrt{16}=4 \Leftrightarrow 4=4 \text { (luôn đúng) }\end{aligned}$$
Vậy giá trị x=2 thỏa mãn phương trình đã cho
Luyện tập 2 trang 26
a) $\sqrt{2 x^2+x+3}=1-x$
b) $\sqrt{3 x^2-13 x+14}=x-3$
Bước 1: Bình phương hai vế và giải phương trình nhận được
Bước 2: Thử lại các giá trị x tìm được ở câu a có thỏa mãn phương trình đã cho hay không và kết luân nghiệm
a) $\sqrt{2 x^2+x+3}=1-x$
Bình phương hai vế của phương trình ta được:
$$2 x^2+x+3=1-2 x+x^2$$
Sau khi thu gọn ta được $x^2+3 x+2=0$. Từ đó $\mathrm{x}=-1$ hoặc $\mathrm{x}=-2$
Thay lần lượt hai giá trị này của x vào phương trình đã cho ta thấy cả hai giá trị $x=-1; x=-2$ đều thỏa mãn Vậy phương trình có tập nghiệm $S=\{-1 ;-2\}$
b) $\sqrt{3 x^2-13 x+14}=x-3$
Bình phương hai vế của phương trình ta được: $3 x^2-13 x+14=x^2-6 x+9$
Sau khi thu gọn ta được $2 x^2-7 x+5=0$. Từ đó $x=1$ hoặc $x=\frac{5}{2}$
Thay lần lượt hai giá trị này của x vào phương trình đã cho ta thấy không có giá trị nào của x thỏa mãn
Vậy phương trình vô nghiệm
Vận dụng trang 26
Để hai người không phải chờ nhau thì thời gian chèo thuyền bằng thời gian kéo xe => lập phương trình.
Giải phương trình này sẽ tìm được vị trí hai người dự định gặp nhau.
Giả sử bác Việt chèo thuyền cập bến ở vị trí $\mathrm{M}$ và ta đặt $\mathrm{BM}=\mathrm{x}(\mathrm{km})(\mathrm{x}>0)$
Ta có: $M C=B C-B M=9,25-x(\mathrm{~km})$
Thời gian di chuyển của anh Nam đến điểm hẹn gặp nhau là $\frac{9,25-x}{5}$ (giờ)
Tam giác ABM vuông tại B, nên ta có:
$$\begin{aligned}& A M^2=A B^2+B M^2=x^2+16 \\& \Rightarrow A M=\sqrt{x^2+16}(\mathrm{~km})\end{aligned}$$
Thời gian di chuyển của bác Việt đến điểm hẹn găp nhau là: $\frac{\sqrt{x^2+16}}{4}$ (giờ)
Để hai người không phải chờ nhau thì ta có phương trình:
$$\frac{\sqrt{x^2+16}}{4}=\frac{9,25-x}{5} \Leftrightarrow 5 \sqrt{x^2+16}=37-4 x$$
Bình phương hai vế của phương trình trên ta được:
$$\begin{aligned}& 25\left(x^2+16\right)=16 x^2-296 x+1369 \\& \Leftrightarrow 9 x^2+296 x-969=0 \\& \Leftrightarrow x=3 \text { hoặc } x=-\frac{323}{9}\end{aligned}$$
Thử lại ta thấy cả hai giá trị của x đều thỏa mãn
Mà $x>0$ nên ta chọn $x=3$
Vậy vị trí hai người gặp nhau cách bến Bính $3 \mathrm{~km}$ và cách thôn Hoành $6,25 \mathrm{~km}$
Giải bài tập vận dụng trang 27 SGK Toán 10 bài 18
Phần tiếp theo sẽ cung cấp cho các bạn phương pháp cùng lời giải trong phần bài tập trang 27 cực kỳ dễ hiểu và chi tiết. Cùng HocThatGioi rèn luyện và nâng cao kỹ năng giải quyết các vấn đề thực tế thông qua các phương pháp, công thức toán học từ bài Phương trình quy về phương trình bậc hai ở trên.
Bài tập 6.20 trang 27
a) $\sqrt{3 x^{2}-4 x-1}=\sqrt{2 x^{2}-4 x+3}$;
b) $\sqrt{x^{2}+2 x-3}=\sqrt{-2 x^{2}+5}$;
c) $\sqrt{2 x^{2}+3 x-3}=\sqrt{-x^{2}-x+1}$;
d) $\sqrt{-x^{2}+5 x-4}=\sqrt{-2 x^{2}+4 x+2}$.
Bước 1: Bình phương hai vế và giải phương trình nhận được
Bước 2: Thử lại các giá trị $x$ nhận được ở trên có thỏa mãn phương trình đã cho hay không kết luận nghiệm
a) $\sqrt{3 x^2-4 x-1}=\sqrt{2 x^2-4 x+3}$
Bình phương hai vế của phương trình ta được:
$$\begin{aligned}& 3 x^2-4 x-1=2 x^2-4 x+3 \\& \Leftrightarrow x^2=4 \\& \Leftrightarrow x=2 \text { hoặc } x=-2\end{aligned}$$
Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy cả 2 giá trị $x=2 ; x=-2$ thỏa mãn
Vậy tập nghiệm của phương trình là $S=\{-2 ; 2\}$
b) $\sqrt{x^2+2 x-3}=\sqrt{-2 x^2+5}$
Bình phương hai vế của phương trình ta được:
$$\begin{aligned}& x^2+2 x-3=-2 x^2+5 \\& \Leftrightarrow 3 x^2+2 x-8=0 \\& \Leftrightarrow x=-2 \text { hoặc } x=\frac{4}{3}\end{aligned}$$
Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy chỉ có giá trị $x=\frac{4}{3}$ thỏa mãn
Vậy tập nghiệm của phương trình là $x=\frac{4}{3}$
c) $\sqrt{2 x^2+3 x-3}=\sqrt{-x^2-x+1}$
Bình phương hai vế của phương trình ta được:
$$\begin{aligned}& 2 x^2+3 x-3=-x^2-x+1 \\& \Leftrightarrow 3 x^2+4 x-4 \\& \Leftrightarrow x=-2 \text { hoặc } x=\frac{2}{3}\end{aligned}$$
Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy cả 2 giá trị đều không thỏa mãn.
Vậy phương trình vô nghiệm
d) $\sqrt{-x^2+5 x-4}=\sqrt{-2 x^2+4 x+2}$
Bình phương hai vế của phương trình ta được:
$$\begin{aligned}& -x^2+5 x-4=-2 x^2+4 x+2 \\& \Leftrightarrow x^2+x-6=0 \\& \Leftrightarrow x=-3 \text { hoặc } x=2\end{aligned}$$
Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy $x=2$ thỏa mãn.
Vậy nghiệm của phương trình là $x=2$
Bài tập 6.21 trang 27
a) $\sqrt{6 x^{2}+13 x+13}=2 x+4$
b) $\sqrt{2 x^{2}+5 x+3}=-3-x$
c) $\sqrt{3 x^{2}-17 x+23}=x-3$;
d) $\sqrt{-x^{2}+2 x+4}=x-2$
Bước 1: Bình phương hai vế và giải phương trình nhận được
Bước 2: Thử lại các giá trị x tìm được ở câu a có thỏa mãn phương trình đã cho hay không và kết luân nghiệm
a) $\sqrt{6 x^2+13 x+13}=2 x+4$
Binh phương hai vế của phương trình ta được:
6 x^2+13 x+13=4 x^2+16 x+16 \\ \Leftrightarrow 2 x^2-3 x-3=0 \\ \Leftrightarrow x=\frac{3-\sqrt{33}}{4} \text { hoặc } x=\frac{3+\sqrt{33}}{4}
Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy cả 2 giá trị $x=\frac{3-\sqrt{33}}{4}$ và $x=\frac{3+\sqrt{33}}{4}$ đều thỏa mãn.
Vậy tập nghiệm của phương trình là $S=\left\{\frac{3-\sqrt{33}}{4} ; \frac{3+\sqrt{33}}{4}\right\}$
b) $\sqrt{2 x^2+5 x+3}=-3-x$
Bình phương hai vế của phương trình ta được:
$$\begin{aligned}& 2 x^2+5 x+3=9+6 x+x^2 \\& \Leftrightarrow x^2-x-6=0 \\& \Leftrightarrow x=-2 \text { hoặc } x=3\end{aligned}$$
Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy không có giá trị nào thỏa mãn
Vậy phương trình vô nghiệm
c) $\sqrt{3 x^2-17 x+23}=x-3$
Bình phương hai vế của phương trình ta được:
3 x^2-17 x+23=x^2-6 x+9 \\ \Leftrightarrow 2 x^2-11 x+14=0 \\ \Leftrightarrow x=2 \text { hoặc } x=\frac{7}{2}
Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy $x=\frac{7}{2}$ thỏa mãn.
Vậy nghiệm của phương trình là $x=\frac{7}{2}$
d) $\sqrt{-x^2+2 x+4}=x-2$
Bình phương hai vế của phương trình ta được:
-x^2-2 x+4=x^2-4 x+4 \\ \Leftrightarrow 2 x^2-6 x=0 \\ \Leftrightarrow x=0 \text { hoặc } x=3
Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy $x=3$ thỏa mãn
Vậy nghiệm của phương trình là $x=3$
Bài tập 6.22 trang 27
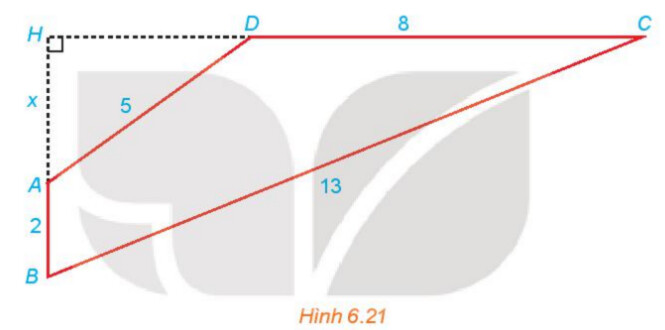
Bước 1: Tính $\mathrm{HD}, \mathrm{HC}$ theo $\mathrm{x}$
Bước 2: Sử dụng định lý py-ta-go cho tam giác vuông $\mathrm{BHC}$
$$B C^2=H B^2+H C^2$$
Khi đó ta lập được phương trình $4 \sqrt{25-x^2}=-x+19$
Bước 3: Giải phương trình trên ta tìm được $x$
Ta có $: \mathrm{AH}=\mathrm{x}(x>0)$
Xét tam giác AHD vuông ở $\mathrm{H}$, ta có:
A D^2=A H^2+H D^2 \\\\ \Leftrightarrow H D^2=A D^2-A H^2=25-x^2 \\ \Rightarrow H D=\sqrt{25-x^2} \\ \text { Ta có: } H C=H D+D C=\sqrt{25-x^2}+8 \\ H B=A H+A B=x+2
Xét tam giác $\mathrm{HBC}$ vuông tại $\mathrm{H}$, ta có:
B C^2=H B^2+H C^2 \\ \Leftrightarrow 13^2=(x+2)^2+\left(\sqrt{25-x^2}+8\right)^2 \\ \Leftrightarrow 169=x^2+4 x+4+25-x^2+16 \sqrt{25-x^2}+64 \\ \Leftrightarrow 16 \sqrt{25-x^2}=-4 x+76 \\ \Leftrightarrow 4 \sqrt{25-x^2}=-x+19
Bình phương hai vế của phương trình trên ta được:
$$\begin{aligned}& 16\left(25-x^2\right)=x^2-38 x+361 \\&\Leftrightarrow 17 x^2-38 x-39=0 \\& \Leftrightarrow x=3 \text { hoặc } x=\frac{-13}{17}\end{aligned}$$
Thay lần lượt các giá trị trên vào phương trình, ta thấy hai giá trị đều thỏa mãn
Do $x>0$ nên ta chọn $x=3 \Rightarrow A H=3$
$$\begin{aligned}& H D=\sqrt{25-3^2}=4 \\& H C=4+8=12 \\& H B=3+2=5\end{aligned}$$
Diện tích tam giác HAD là $S_1=\frac{1}{2} \cdot H A \cdot H D=\frac{1}{2} \cdot 3 \cdot 4=6$
Diện tích tam giác $\mathrm{HBC}$ là $S_2=\frac{1}{2} . H B \cdot H C=\frac{1}{2} \cdot 5 \cdot 12=30$
Vậy diện tích tứ giác ABCD là $S=S_2-S_1=30-6=24$
Bài tập 6.23 trang 27
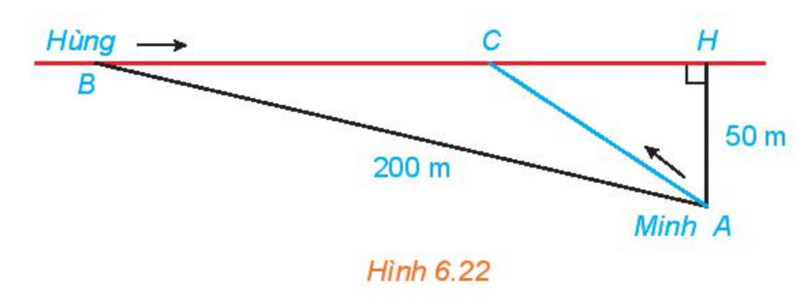
Bước 1: Đặt $\mathrm{CH}=\mathrm{x}(\mathrm{km})(x>0)$
Bước 2: Tính quãng đường Minh di chuyển, Hùng di chuyến
Bước 3: Để hai người không phải chờ nhau thì thời gian đi của 2 bạn phải bằng nhau nên ta lập được phương trình:
$$\frac{\sqrt{0,0025+x^2}}{5}=\frac{\sqrt{15}-20 x}{300}$$
Giải phương trình tìm được $x$ là tìm được vị trí điểm $C$
Đổi: $200 \mathrm{~m}=0,2 \mathrm{~km}$
$50 \mathrm{~m}=0,05 \mathrm{~km}$
Đặt $\mathrm{CH}=x(\mathrm{~km})(x>0)$
Xét tam giác CHA vuông ở H, ta có:
$$C A^2=C H^2+A H^2=x^2+0,0025$$
$\Rightarrow$ Quãng đường Minh di chuyến là $C A=\sqrt{x^2+0,0025}$
Vận tốc đi bộ của Minh là $5 \mathrm{~km} / \mathrm{h}$ nên thời gian di chuyến của Minh là:
$$\frac{\sqrt{x^2+0,0025}}{5}(giờ)$$
Xét tam giác AHB xuông tại $\mathrm{H}$, ta có:
HB^2=A B^2-A H^2=(0,2)^2-(0,05)^2=0,0375 \\ \Rightarrow HB=\frac{\sqrt{15}}{20}
$\Rightarrow$ Quãng đường mà Hùng di chuyển là: $B C=H B-H C=\frac{\sqrt{15}}{20}-x$
Vận tốc đạp xe của Hùng là $15 \mathrm{~km} / \mathrm{h}$ nên thời gian di chuyến của Hùng là:
$$\frac{\frac{\sqrt{55}}{20}-x}{15}=\frac{\sqrt{15}-20 x}{300} \text { (giờ) }$$
Để hai bạn không phải chờ nhau thì:
$$\begin{aligned}& \frac{\sqrt{x^2+0,0025}}{5}=\frac{\sqrt{15}-20 x}{300} \\& \Leftrightarrow 60 \sqrt{x^2+0,0025}=\sqrt{15}-20 x\end{aligned}$$
Bình phương hai vế của phương trình trên ta được:
$$\begin{aligned}& 3600\left(x^2+0,0025\right)=15-40 \sqrt{15} x+400 x^2 \\& \Leftrightarrow 3200 x^2+40 \sqrt{15} x-6=0 \\& \Leftrightarrow x=\frac{-\sqrt{15}-3 \sqrt{7}}{160} \text { hoặc } x=\frac{-\sqrt{15}+3 \sqrt{7}}{160}\end{aligned}$$
Thay lần lượt các giá trị này vào phương trình đầu, ta thấy cả 2 giá trị đều thỏa mãn
Do $x>0$ nên ta chọn $x=\frac{-\sqrt{15}+3 \sqrt{7}}{160}$
$$\Rightarrow B C=B H-C H=\frac{\sqrt{15}}{20}-\frac{-\sqrt{15}+3 \sqrt{7}}{160} \approx 0,1682(\mathrm{~km})=168,2(m)$$
Vậy vị trí C thỏa mãn đề bài là điểm cách B khoảng $168,2 \mathrm{~m}$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Phương trình quy về phương trình bậc hai Chương Hàm số, đồ thị và ứng dụng Toán 10 Kết nối tri thức tập 2 ở các trang 25, 26, 27. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!





