Giải SGK bài tập cuối chương VI Toán 10 Kết nối tri thức Tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi trắc nghiệm cũng như bài tập tự luận trong bài tập cuối chương VI. Đây là Bài tập cuối chương VI trang 28, 29 sách Toán 10 Kết nối tri thức tập 2. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi trắc nghiệm trong SGK của bài tập cuối chương VI
Sau khi đã học lý thuyết và giải các bài tập ở Chương Hàm số, đồ thị và ứng dụng. Cùng HocThatGioi giải chi tiết phần câu hỏi trắc nghiệm ở trang 28 trong bài tập cuối chương VI ngay sau đây nhé!
Bài 6.24 trang 28
A. $D=[2 ;+\infty)$.
B. $D=(2 ;+\infty)$.
C. $D=\mathbb{R} \backslash\{2\}$.
D. $D=\mathbb{R}$.
– Giải bất phương trình $x-2>0$.
– Kết luận tập xác định của hàm số.
Để hàm số $y=\frac{1}{\sqrt{x-2}}$ xác định $\Leftrightarrow x-2>0 \Leftrightarrow x>2$.
Vậy tập xác định của hàm số là: $D=(2 ;+\infty)$.
Chọn B.
Bài 6.25 trang 28
A. $I(-1 ; 0)$.
B. $I(3 ; 0)$.
C. $I(0 ; 3)$.
D. $I(1 ; 4)$.
– Xác định các hệ số $a, b, c$
– Tính $\Delta$.
– Xác định tọa độ đỉnh $I\left(-\frac{b}{2 a} ;-\frac{\Delta}{4 a}\right)$.
Parabol $y=-x^2+2 x+3$ có $a=-1 ; b=2 ; c=3$.
Ta có: $\Delta=b^2-4 a c=2^2-4(-1) .3=4+12=16$.
Tọa độ đỉnh $I$ là: $I(1 ; 4)$.
Chọn D.
Bài 6.26 trang 28
A. Đồng biến trên khoảng $(1 ;+\infty)$.
B. Đồng biến trên khoảng $(-\infty ; 4)$.
C. Nghịch biến trên khoảng $(-\infty ; 1)$.
D. Nghịch biến trên khoảng $(1 ; 4)$.
– Xác định trục đối xứng $x=-\frac{b}{2 a}$ của hàm số
– Xác định khoảng đồng biến, nghịch biến của hàm số
Trục đối xứng của hàm số là: $x=\frac{5}{2}$.
Vì $a=1>0$ nên hàm số đồng biến trên khoảng $\left(\frac{5}{2} ;+\infty\right)$ và nghịch biến trên khoảng $\left(-\infty ; \frac{5}{2}\right)$.
Chọn C.
Bài 6.27 trang 28
A. $m=-1$.
B. $m=-2$.
C. $m=2$.
D. $m>2$.
– Tính $\Delta=b^2-4 a c$.
– Giải bất phương trình $\Delta<0$ để bất phương trình có nghiệm đúng với mọi $x \in \mathbb{R}$
Để $x^2-2 m x+4>0$ nghiệm đúng với mọi $x \in \mathbb{R}$
$\Leftrightarrow \Delta^{\prime}<0$
$\Leftrightarrow(-m)^2-4<0$
$\Leftrightarrow m^2-40$ nên ta có bảng xét dấu sau:

Chọn A.
Bài 6.28 trang 28
A. $\{-1-\sqrt{5} ;-1+\sqrt{5}\}$.
B. $\{-1-\sqrt{5}\}$.
C. $\{-1+\sqrt{5}\}$.
D. $\varnothing$.
– Tìm điều kiện để phương trình có nghĩa
– Bình phương hai vế của phương trình để mất dấu căn
– Đưa về dạng phương trình và giải: $a x^2+b x+c=0$.
ĐК: $x-1 \geq 0 \Leftrightarrow x \geq 1$
$\Rightarrow$ TXĐ của phương trình là: $D=[1 ;+\infty)$
Giải phương trình: $\sqrt{2 x^2-3}=x-1$
$$\begin{aligned}& \Leftrightarrow\left(\sqrt{2 x^2-3}\right)^2=(x-1)^2 \\& \Leftrightarrow 2 x^2-3=x^2-2 x+1 \\& \Leftrightarrow x^2+2 x-4=0 \\& \Leftrightarrow\left[\begin{array}{l}x=-1+\sqrt{5} \\x=-1-\sqrt{5}\end{array}\right.\end{aligned}$$
Ta thấy $x=-1+\sqrt{5}$ thỏa mãn.
Vậy tập nghiệm của phương trình là: $S=\{-1+\sqrt{5}\}$
Chọn C.
Trả lời câu hỏi tự luận trong SGK của bài tập cuối chương VI
Phần tiếp theo sẽ cung cấp cho các bạn phương pháp cùng lời giải trong phần câu hỏi tự luận trang 28, 29 cực kỳ dễ hiểu và chi tiết. Cùng HocThatGioi rèn luyện và nâng cao kỹ năng giải quyết các vấn đề thực tế thông qua các phương pháp, công thức toán học từ Chương Hàm số, đồ thị và ứng dụng.
Bài 6.29 trang 28
a) $y=\sqrt{2 x-1}+\sqrt{5-x}$
b) $y=\frac{1}{\sqrt{x-1}}$.
– Giải bất phương trình $\left\{\begin{array}{c}2 x-1 \geq 0 \\ 5-x \geq 0\end{array}\right.$ và $x-1>0$.
– Kết luận tập xác định của hàm số
a) Tập xác định của hàm số $y=\sqrt{2 x-1}+\sqrt{5-x}$ là:
\begin{cases} 2x-1 \geq 0 \\ 5-x \geq 0 \\ \end{cases} \Longleftrightarrow \begin{cases} x \geq \frac{\mathrm{1} }{\mathrm{2} } \\ x \leq 5 \\ \end{cases} \Longleftrightarrow \frac{\mathrm{1} }{\mathrm{2}} \leq x \leq 5
Vậy tập xác định của hàm số là: $D=\left[\frac{1}{2} ; 5\right]$.
b) Tập xác định của hàm số $y=\frac{1}{\sqrt{x-1}}$ là: $x-1>0 \Leftrightarrow x>1$.
Vậy tập xác định của hàm số là: $D=(1 ;+\infty)$.
Bài 6.30 trang 28
a) $y=-x^2+6 x-9$
b) $y=-x^2-4 x+1$
c) $y=x^2+4 x$
d) $y=2 x^2+2 x+1$.
Cho hàm số $y=a x^2+b x+c$
– Xác định tọa độ đỉnh $I\left(\frac{-b}{a} ; \frac{-\Delta}{4 a}\right)$
– Trục đối xứng $x=\frac{-b}{a}$
– Giao với trục $O x, O y$.
– Xác định tập giá trị của hàm số
– Từ đồ thị tìm khoảng đồng biến, nghịch biến của hàm số
a) $y=-x^2+6 x-9$
Ta có: $a=-1$ nên parabol quay bề lõm xuống dưới.
– Đỉnh $I(3 ; 0)$.
– Trục đối xứng $x=3$.
– Giao điểm của đồ thị với trục $O y$ là: $A(0 ;-9)$.
– Parabol cắt trục hoành tại $x=3$.
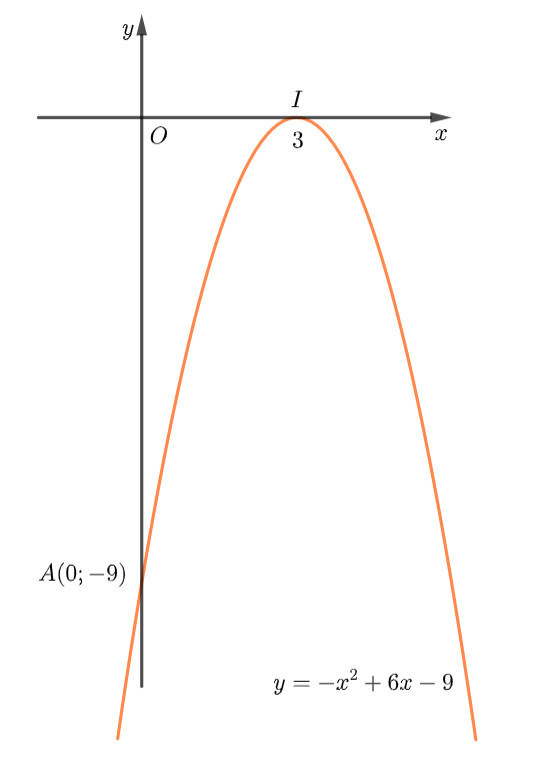
Từ đồ thị ta thấy: Hàm số $y=-x^2+6 x-9$ đồng biến trên khoảng $(-\infty ; 3)$ và nghịch biến trên khoảng $(3 ;+\infty)$.
b) $y=-x^2-4 x+1$
Ta có: $a=-1$ nên parabol quay bề lõm xuống dưới.
– Đỉnh $I(-2 ; 5)$.
– Trục đối xứng $x=-2$.
– Giao điểm của hàm số với trục $O y$ là: $(0 ; 1)$.
– Giao điểm của hàm số với trục $O x$ là: $x=-2+\sqrt{5}$ và $x=-2-\sqrt{5}$.
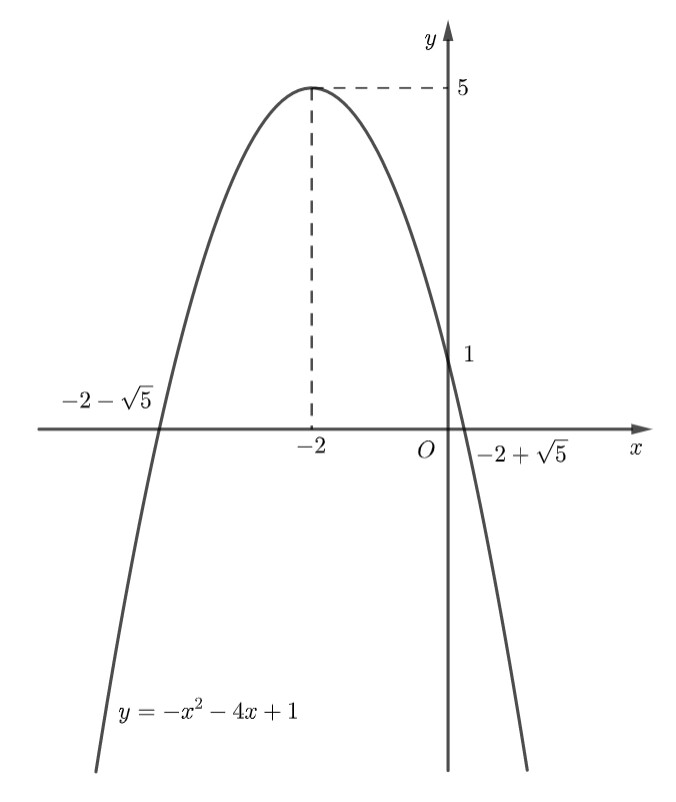
Từ đồ thị ta thấy: Hàm số $y=-x^2-4 x+1$ đồng biến trên khoảng $(-\infty ;-2)$ và nghịch biến trên khoảng $(-2 ;+\infty)$.
c) $y=x^2+4 x$
Ta có: $a=1>0$ nên parabol quay bề lõm lên trên.
– Đỉnh $I(-2 ;-4)$.
– Trục đối xứng $x=-2$.
– Giao điểm của hàm số với trục $O y$ là: $(0 ; 0)$.
– Giao điểm của hàm số với trục $O x$ là: $x=0$ và $x=-4$.
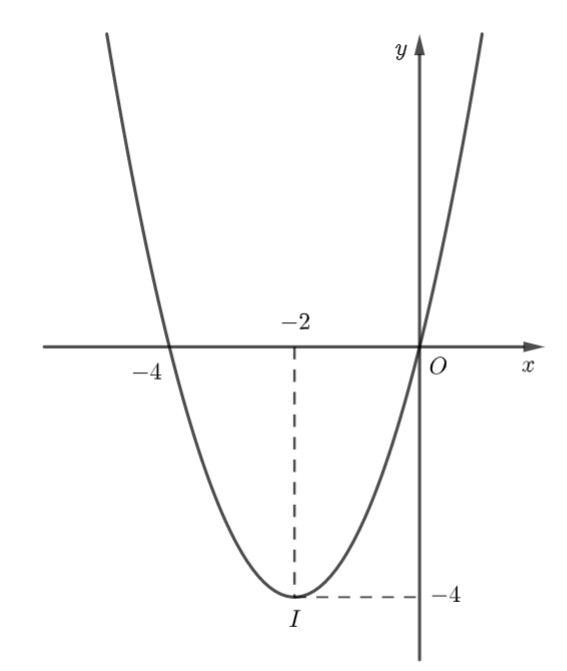
Từ đồ thị ta thấy: Hàm số $y=x^2+4 x$ đồng biến trên khoảng $(-2 ;+\infty)$ và nghịch biến trên khoảng $(-\infty ;-2)$.
d) $y=2 x^2+2 x+1$
Ta có: $a=2>0$ nên parabol quay bề lõm lên trên.
– Đỉnh $I\left(-\frac{1}{2} ; \frac{1}{2}\right)$.
– Trục đối xứng $x=-\frac{1}{2}$.
– Giao điểm của hàm số với trục $O y$ là: $(0 ; 1)$.
– Đồ thị hàm số không có giao điểm với trục $O x$. Lấy điểm (1;5) thuộc đồ thị hàm số, điểm đối xứng với điểm đó qua trục đối xứng $x=-\frac{1}{2}$ là: $(-2 ; 5)$.
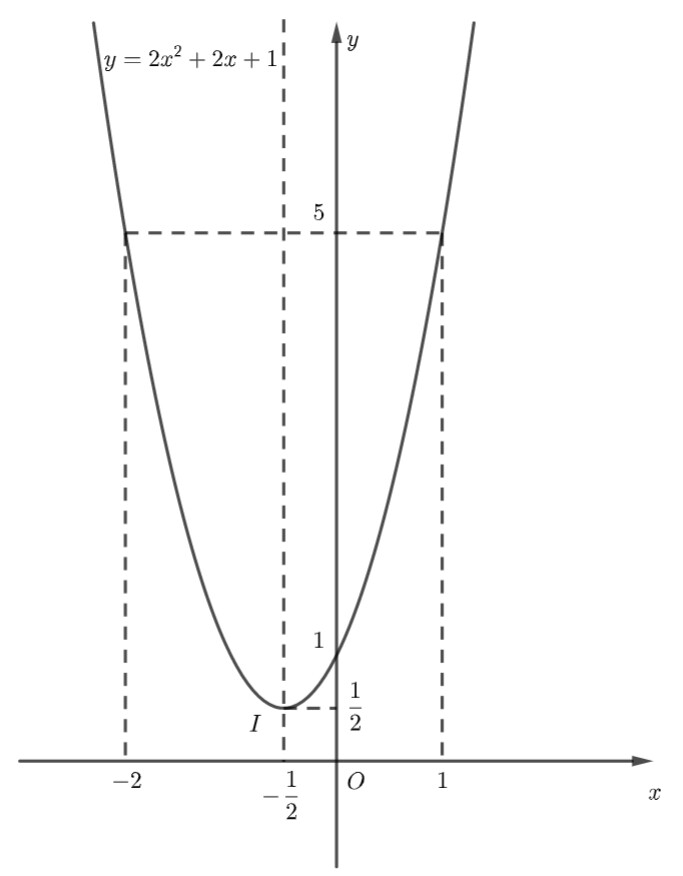
Từ đồ thị ta thấy: Hàm số $y=2 x^2+2 x+1$ đồng biến trên khoảng $\left(-\frac{1}{2} ;+\infty\right)$ và nghịch biến trên khoảng $\left(-\infty ;-\frac{1}{2}\right)$.
Bài 6.31 trang 28
a) $(P)$ đi qua hai điểm $A(1 ; 1)$ và $B(-1 ; 0)$;
b) $(P)$ đi qua điểm $M(1 ; 2)$ và nhận đường thẳng $x=1$ làm trục đối xứng;
c) $(P)$ có đỉnh là $/(1 ; 4)$.
a) Thay các điểm $A(1 ; 1)$ và $B(-1 ; 0)$ vào parabol $(P)$ để giải hệ phương trình tìm $a, b$.
b) Thay điểm $M(1 ; 2)$ vào parabol $(P)$ và trục đối xứng $x=-\frac{b}{2 a}=1$ để giải hệ phương trình tìm $a, b$.
c) Thay đỉnh $I(1 ; 4)$ vào parabol $(P)$ và trục đối xứng $x=-\frac{b}{2 a}=1$ để giải hệ phương trình tìm $a, b$.
a) Theo giả thiết, hai điểm $A(1 ; 1)$ và $B(-1 ; 0)$ thuộc parabol $(P): y=a x^2+b x+3$ nên ta có: $\left\{\begin{array}{l}a+b+3=1 \\ a-b+3=0\end{array} \Leftrightarrow\left\{\begin{array}{l}a=\frac{-5}{2} \\ b=\frac{1}{2}\end{array}\right.\right.$
Vậy hàm số cần tìm là: $y=-\frac{5}{2} x^2+\frac{1}{2} x+3$.
b) Parabol nhận $x=1$ làm trục đối xứng nên $-\frac{b}{2 a}=1 \Leftrightarrow b=-2 a$.
Điếm $M(1 ; 2)$ thuộc parabol nên $a+b+3=2 \Leftrightarrow a+b=-1$.
Do đó, ta có hệ phương trình: $\left\{\begin{array}{c}b=-2 a \\ a+b=-1\end{array} \Leftrightarrow\left\{\begin{array}{c}a=1 \\ b=-2\end{array}\right.\right.$
Vậy hàm số cần tìm là: $y=x^2-2 x+3$
c) Parabol có đỉnh $I(1 ; 4)$ nên ta có:
\begin{cases} \frac{\mathrm{-b} }{\mathrm{2} a} =1 \\ a+b+3=4 \\\end{cases} \Longleftrightarrow \begin{cases} b=-2a \\ a+b=1 \\ \end{cases} \Longleftrightarrow \begin{cases} a=-1 \\ b=2 \\ \end{cases}
Vậy hàm số cần tìm là: $y=-x^2+2 x+3$.
Bài 6.32 trang 28
a) $2 x^{2}-3 x+1>0$;
b) $x^{2}+5 x+4<0$;
c) $-3 x^{2}+12 x-12 \geq 0$;
d) $2 x^{2}+2 x+1<0$.
– Tìm nghiệm của các phương trình trên
– Lập bảng xét dấu
– Kết luận tập nghiệm của bất phương trình
Tam thức $f(x)=2 x^2-3 x+1$ có $a+b+c=2-3+1=0$ nên hai nghiệm phân biệt $x_1=1$ và $x_2=\frac{1}{2}$.
Mặt khác $a=2>0$, do đó ta có bảng xét dấu sau:


c) $-3 x^2+12 x-12 \geq 0$
Tam thức $f(x)=-3 x^2+12 x-12=-3\left(x^2-4 x+4\right)=-3(x-2)^2 \leq 0$
Do đó:
-3 x^2+12 x-12 \geq 0 \\\\ \Leftrightarrow-3 x^2+12 x-12=0 \\\\ \Leftrightarrow-3(x-2)^2=0 \\\\ \Leftrightarrow x=2 .
Tập nghiệm của bất phương trình là: $S=(2)$.
d) $2 x^2+2 x+1<0$.
Tam thức $f(x)=2 x^2+2 x+1$ có $\Delta=-10$ nên $f(x)$ luôn dương với mọi $x$, tức là $2 x^2+2 x+1>0$ với mọi $x \in \mathbb{R}$.
$\Rightarrow$ bất phương trình vô nghiệm
Bài 6.33 trang 29
a) $\sqrt{2 x^{2}-14}=x-1$
b) $\sqrt{-x^{2}-5 x+2}=\sqrt{x^{2}-2 x-3}$.
– Tìm tập xác định của phương trình
– Bình phương hai vế của phương trình để mất dấu căn
– Đưa về dạng phương trình $a x^2+b x+c=0$
a) $\sqrt{2 x^2-14}=x-1$
ĐK: $x-1 \geq 0 \Leftrightarrow x \geq 1$.
$\Rightarrow$ TXĐ: $D=[1 ;+\infty)$
(1) $\Leftrightarrow\left(\sqrt{2 x^2-14}\right)^2=(x-1)^2$
$\Leftrightarrow 2 x^2-14=x^2-2 x+1$
$\Leftrightarrow x^2+2 x-15=0$
$\Leftrightarrow\left[\begin{array}{c}x=3 \\ x=-5\end{array}\right.$
Nhận thấy $x=3$ thỏa mãn điều kiện
Vậy nghiệm của phương trình (1) là: $x=3$
b) $\sqrt{-x^2-5 x+2}=\sqrt{x^2-2 x-3}$ (2)
ĐK: \begin{cases} -x^2-5x+2 \geq 0 \\ x^2-2x-3 \geq 0 \\ \end{cases} \Longleftrightarrow \frac{\mathrm{-5- \sqrt{33} } }{\mathrm{2} } \leq x \leq 1
(2) $\Leftrightarrow\left(\sqrt{-x^2-5 x+2}\right)^2=\left(\sqrt{x^2-2 x-3}\right)^2$
$\Leftrightarrow-x^2-5 x+2=x^2-2 x-3$
$\Leftrightarrow 2 x^2+3 x-5=0$
$\Leftrightarrow\left[\begin{array}{c}x=1 \\ x=-\frac{5}{2}\end{array}\right.$
Nhận thấy $x=-\frac{5}{2}$ thỏa mãn điều kiện
Vậy nghiệm của phương trình (2) là: $x=-\frac{5}{2}$
Bài 6.34 trang 29
Giả sử $t$ là thời gian (theo đơn vị năm) tính từ năm 2018. Số lượng loại máy tính đó bán được trong năm 2018 và năm 2019 lần lượt được biểu diễn bởi các điểm $(0 ; 3,2)$ và $(1 ; 4)$. Giả sử điểm $(0 ; 3,2)$ là đỉnh đồ thị của hàm số bậc hai này.
a) Lập công thức của hàm số mô tả số lượng máy tính xách tay bán được qua từng năm.
b) Tính số lượng máy tính xách tay đó bán được trong năm 2024.
c) Đến năm bao nhiêu thì số lượng máy tính xách tay đó bán được trong năm sẽ vượt mức 52 nghìn chiếc?
– Gọi hàm số bậc hai cần tìm là: $y=a t^2+b t+c$.
– Tọa độ đỉnh $I(0 ; 3,2)$ và đi qua điểm $(1 ; 4)$ từ đó tìm ra được $a, b, c$.
– Tính số lượng máy tính bán xách tay bán ra trong năm 2024 ứng với $t=6$
– Giải phương trình $52=a t^2+b t+c$ để tìm ra số năm.
a) Gọi hàm số bậc hai cần tìm là: $y=a t^2+b t+c$.
Ta có: đỉnh $I(0 ; 3,2)$ và đi qua điểm $(1 ; 4)$
Nên \begin{cases} \frac{\mathrm{-b} }{\mathrm{2} a}=0 \\ c=0,2 \\ a+b+c=4 \end{cases} \Longleftrightarrow \begin{cases} b=0 \\ c=3,2 \\ a+c=4 \end{cases} \Longleftrightarrow \begin{cases} a=0,8 \\ b=0 \\ c=3,2 \end{cases}
Vậy hàm số cần tìm là: $y=0,8 t^2+3,2$
b) Thời gian từ năm 2018 đến năm 2024 là: $t=2024-2018=6$ năm
Số lượng máy tính xách tay bán được trong năm 2024 là:
$0,8.6^2+3,2=32$ (nghìn chiếc).
c) Năm bán được vượt mức 52 nghìn chiếc máy tính là:
0,8 t^2+3,2>52 \\ \Leftrightarrow 0,8 t^2-48,8>0 \\ \Leftrightarrow t \in(-\infty ;-\sqrt{61}) \cup(\sqrt{61} ;+\infty) \\ \text { Vì } t>0 \text { nên } t \in(\sqrt{61} ;+\infty) \text { hay } t>\sqrt{61} \approx 7,8
Từ năm thứ 8 hay năm 2026 thì số lượng máy tính xách tay bán ra vượt mức 52 nghìn chiếc.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK Bài tập cuối chương Hàm số, đồ thị và ứng dụng Toán 10 Kết nối tri thức tập 2 ở các trang 28, 29. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!





