Giải SGK bài 17 chương VI trang 19, 20, 21, 22, 23, 24 Toán 10 Kết nối tri thức tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Dấu của tam thức bậc hai. Đây là bài học thuộc bài 17 chương VI trang 19, 20, 21, 22, 23, 24 sách Toán 10 Kết nối tri thức tập 2. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi trong SGK của bài 17
Dưới đây là phương pháp và bài giải chi tiết cho câu hỏi mở đầu, các hoạt động cùng phần luyện tập ở các trang 19, 20, 21, 22, 23 trong bài Dấu của tam thức bậc hai. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Câu hỏi mở đầu trang 19
Theo Bài 16 , diện tích mảnh đất được rào chắn là $S(x)=-2 x^2+20 x\left(\mathrm{~m}^2\right)$.
Vì mảnh đất được rào chắn có diện tích không nhỏ hơn $48 \mathrm{~m}^2$ nghĩa là $\mathrm{S}(\mathrm{x})$ phải lớn hơn hoặc bằng 48 .
Khi đó: $-2 x^2+20 x \geq 48 \Leftrightarrow 2 x^2-20 x+48 \leq 0$ (1).
Ta cần giải bất phương trình (1).
Sau bài học này ta sẽ giải được bất phương trình (1) như sau:
Tam thức bậc hai $f(x)=2 x^2-20 x+48$ có hai nghiệm $x_1=4 ; x_2=6$; hệ số $a=2>0$. Từ đó suy ra tập nghiệm của bất phương trình (1) là đoạn $[4 ; 6]$. Như vậy khoảng cách từ điểm cắm cột đến bờ tường phải lớn hơn hoặc bằng $4 \mathrm{~m}$ và nhỏ hơn hoặc bằng $6 \mathrm{~m}$ thì mảnh đất rào chắn của bác Việt sẽ có diện tích không nhỏ hơn $48 \mathrm{~m}^2$.
Hoạt động 1 trang 19
$$\begin{aligned}& A=0,5 x^2 \\& B=1-x^2 \\& C=x^2+x+1 \\& D=(1-x)(2 x+1)\end{aligned}$$
Ta có :
A=0,5 x^2 \\B=1-x^2 \\C=x^2+x+1 \\ D=(1-x)(2 x+1)=2 x+1-2 x^2-x=-2 x^2+x+1
=> Các biểu thức đều có dạng $a x^2+b x+c(a \neq 0), \mathrm{a}, \mathrm{b}, \mathrm{c}$ là các số thực.
Luyện tập 1 trang 19
$$\begin{aligned}& A=3 x+2 \sqrt{x}+1 \\& B=-5 x^4-3 x^2+4 \\& C=-\frac{2}{3} x^2+7 x-4 \\& D=\left(\frac{1}{x}\right)^2+2 \cdot \frac{1}{x}+3\end{aligned}$$
Tam thức bậc hai là biểu thức có dạng $a x^2+b x+c$, trong đó $a, b, c$ là những số cho trước $(a \neq 0)$
Biểu thức $C=-\frac{2}{3} x^2+7 x-4$ là tam thức bậc hai
Biểu thức $\mathrm{A}$ không là tam thức bậc hai vì chứa $\sqrt{x}$
Biểu thức $\mathrm{B}$ không là tam thức bậc hai vì chứa $x^4$
Biểu thức $D$ không là tam thức bậc hai vì chứa $\left(\frac{1}{x}\right)^2$
Hoạt động 2 trang 19
a) Xác định hệ số a. Tính $f(0) ; f(1) ; f(2) ; f(3) ; f(4)$ và nhận xét về dấu của chúng so với dấu của hệ số a
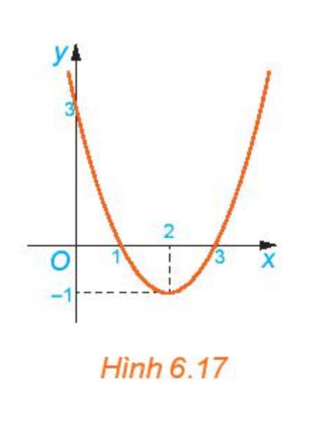
b) Cho đồ thị hàm số $\mathrm{y}=\mathrm{f}(\mathrm{x})(\mathrm{H} .6 .17)$. Xét từng khoảng $(-\infty ; 1) ;(1 ; 3) ;(3 ;+\infty)$, đồ thị nằm phía trên hay phía dưới trục $\mathrm{Ox}$ ?
c) Nhận xét về dấu của $f(x)$ và dấu của hệ số a trên từng khoảng đó.
a) Hệ số a là: $a=1$
$$\begin{aligned}& f(0)=0^2-4.0+3=3 \\& f(1)=1^2-4.1+3=0 \\& f(2)=2^2-4.2+3=-1 \\& f(3)=3^2-4.3+3=0 \\& f(4)=4^2-4.4+3=3\end{aligned}$$
=> $f(0); f(4)$ cùng dấu với hệ số a; $f(2)$ khác dấu với hệ số a
b) Nhìn vào đồ thị ta thấy
– Trên khoảng $(-\infty ; 1)$ đồ thị nằm phía trên trục hoành
– Trên khoảng ( $1 ; 3)$, đồ thị nằm phía dưới trục hoành
– Trên khoảng $(3 ;+\infty)$, đồ thị nằm phía trên trục hoành
c) – Trên khoảng $(-\infty ; 1)$ đồ thị nằm phía trên trục hoành $=>\mathrm{f}(x)>0$, cùng dấu với hệ số a
– Trên khoảng $(1 ; 3)$, đồ thị nằm phía dưới trục hoành $=>\mathrm{f}(\mathrm{x})\mathrm{f}(\mathrm{x})>0$, cùng dấu với hệ số a
Hoạt động 3 trang 20
a) Xét trên từng khoảng $(-\infty ;-1),\left(-1 ; \frac{3}{2}\right),\left(\frac{3}{2} ;+\infty\right)$, đồ thị nằm phía trên trục $\mathrm{Ox}$ hay nằm phía dưới trục $\mathrm{Ox}$
b) Nhận xét về dấu của $\mathrm{g}(\mathrm{x})$ và dấu của hệ số a trên từng khoảng đó
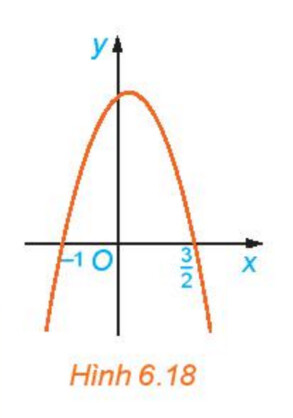
Ta có: hệ số $a=-2f(x)f(x)>0$, khác dấu với hệ số a
– Trên khoảng $\left(\frac{3}{2} ;+\infty\right)$, đồ thị nằm phía dưới trục hoành $=>f(x)<0$, cùng dấu với hệ số a
Hoạt động 4 trang 20
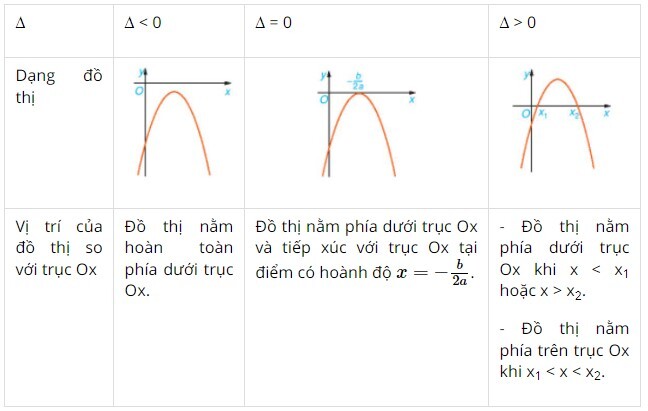
Trường hợp a>0
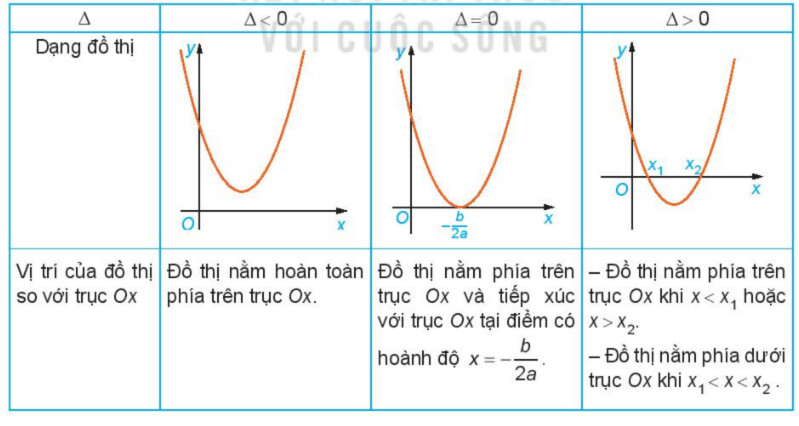
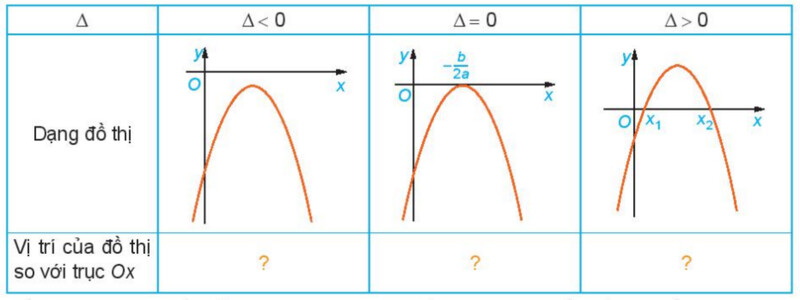
Luyện tập 2 trang 22
a) $-3 x^{2}+x-\sqrt{2}$
b) $x^{2}+8 x+16$
c) $-2 x^{2}+7 x-3$.
Bước 1: Tính $\Delta=b^2-4 a c$
Bước 2:
– Nếu $\Delta0$ thì $f(x)$ có 2 nghiệm là x_1; x_2 (x_1 \lt x_2). Ta lập bảng xét dấu.

a) $f(x)=-3 x^2+x-\sqrt{2}$ có $\Delta=1-12 \sqrt{2}<0$ và a $=-3<0$ nên $f(x)0$ nên $g(\mathrm{x})$ có nghiệm kép $x=-4$ và $g(\mathrm{x})>0$ với mọi $x \neq-4$
c) $h(x)=-2 x^2+7 x-3$ có $\Delta=25>0$ và $a=-2<0$ và có 2 nghiệm phân biệt $x_1=\frac{1}{2} ; x_2=3$
Do đó ta có bảng xét dấu h(x)

Hoạt động 5 trang 22
Diện tích mảnh đất được rào chắn là $S(x)=-2 x^2+20 x\left(m^2\right)$.
Vì mảnh đất được rào chắn có diện tích không nhỏ hơn $48 \mathrm{~m}^2$ nghĩa là $\mathrm{S}(\mathrm{x})$ phải lớn hơn hoặc bằng 48 .
Khi đó: $-2 x^2+20 x \geq 48$.
Luyện tập 3 trang 23
а) $-5 x^2+x-1 \leq 0$
b) $x^2-8 x+16 \leq 0$
c) $x^2-x+6>0$
Xét dấu tam thức bậc hai $f(x)=a x^2+b x+c$
Bước 1: Tính $\Delta=b^2-4 a c$
Bước 2:
– Nếu $\Delta0$ thì $f(x)$ có 2 nghiệm là x_1; x_2 (x_1 \lt x_2). Ta lập bảng xét dấu:

a) Tam thức $f(x)=-5 x^2+x-1$ có $\Delta=-19<0$, hệ số $a=-5<0$ nên $\mathrm{f}(\mathrm{x})$ luôn âm (cùng dấu với a) với mọi x, tức là $-5 x^2+x-10$ nên $g(x)$ luôn dương (cùng dấu với a) với mọi $x \neq 4$, tức là $x^2-8 x+16>0$ với mọi $x \neq 4$
Suy ra bất phương trình có nghiệm duy nhất là $x=4$
c) Tam thức $h(x)=x^2-x+6$ có $\Delta=-230$ nên $\mathrm{h}(\mathrm{x})$ luôn dương (cùng dấu với a) với mọi x , tức là $x^2-x+6>0$ với mọi $x \in \mathbb{R}$. Suy ra bất phương trình có vô số nghiệm
Vận dụng trang 23
Tìm khoảng thời gian $t$ để $h(t)>5$, bài toán đưa về xét dấu tam thức $f(t)=h(t)-5$
Các bước xét dấu tam thức bậc hai $f(t)=a t^2+b t+c$
Bước 1: Tính $\Delta=b^2-4 a c$
Bước 2:
– Nếu $\Delta0$ thì $f(t)$ có 2 nghiệm là x_1; x_2 (x_1 \lt x_2).
Ta lập bảng xét dấu.

Để quả bóng ở độ cao trên $5 \mathrm{~m}$ so với mặt đất thì:
$$\begin{aligned}& h(t)>5 \\& \Rightarrow-4,9 t^2+20 t+1>5 \\& \Rightarrow-4,9 t^2+20 t-4>0\end{aligned}$$
Đặt $f(t)=-4,9 t^2+20 t-4$ có $\Delta^{\prime}=b^{\prime 2}-a c=10^2-(-4,9) .(-4)=80,4>0$ nên $f(t)$ có 2 nghiệm:
t_1= \frac{\mathrm{-b’+ \sqrt{ \Delta’} } }{\mathrm{a}} = \frac{\mathrm{-10+ \sqrt{ 80,4} } }{\mathrm{-4,9}}= \frac{\mathrm{10- \sqrt{ 80,4} } }{\mathrm{4,9}}\\ t_2= \frac{\mathrm{-b’- \sqrt{ \Delta’} } }{\mathrm{a}} = \frac{\mathrm{-10- \sqrt{ 80,4} } }{\mathrm{-4,9}}= \frac{\mathrm{10+ \sqrt{ 80,4} } }{\mathrm{4,9}}
Mặt khác $a=-4,9<0$, do đó ta có bảng xét dấu sau:
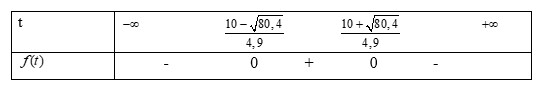
Vậy để quả bóng sẽ ở độ cao trên $5 \mathrm{~m}$ so với mặt đất thì $t \in\left(\frac{10-\sqrt{80,4}}{4,9} ; \frac{10+\sqrt{80,4}}{4,9}\right)$
Giải bài tập vận dụng trang 24 SGK Toán 10 bài 17
Phần tiếp theo sẽ cung cấp cho các bạn phương pháp cùng lời giải trong phần bài tập trang 24 cực kỳ dễ hiểu và chi tiết. Cùng HocThatGioi rèn luyện và nâng cao kỹ năng giải quyết các vấn đề thực tế thông qua các phương pháp, công thức toán học từ bài Dấu của tam thức bậc hai ở trên.
Bài tập 6.15 trang 24
a) $3 x^{2}-4 x+1$;
b) $x^{2}+2 x+1$;
c) $-x^{2}+3 x-2$
d) $-x^{2}+x-1$
Xét dấu tam thức bậc hai $f(x)=a x^2+b x+c$
Bước 1: Tính $\Delta=b^2-4 a c$
Bước 2:
– Nếu $\Delta0$ thì $f(x)$ có 2 nghiệm là x_1; x_2 (x_1 \lt x_2).
Ta lập bảng xét dấu:

a) $f(x)=3 x^2-4 x+1$ có $\Delta=4>0, a=3>0$ và có hai nghiệm phân biệt $x_1=1 ; x_2=\frac{1}{3}$. Do đó ta có bảng xét dấu $f(x)$ :
Suy ra $f(x)>0$ 0ới mọi $x \in\left(-\infty ; \frac{1}{3}\right) \cup(1 ;+\infty)$ và $f(x)<0$ với mọi $x \in\left(\frac{1}{3} ; 1\right)$

b) $g(x)=x^2+2 x+1$ có $\Delta=0$ và $a=1>0$ nên $g(x)$ có nghiệm kép $x=-1$ và $g(x)>0$ với $x \neq-1$
c) $h(x)=-x^2+3 x-2$ có $\Delta=1>0, a=-1$

Suy ra $h(x)>0$ với mọi $x \in(1 ; 2)$ và $h(x)<0$ với mọi $x \in(-\infty ; 1) \cup(2 ;+\infty)$
d) $k(x)=-x^2+x-1$ có $\Delta=-3$
Bài tập 6.16 trang 24
a) $x^{2}-1 \geq 0$;
b) $x^{2}-2 x-1<0$;
c) $-3 x^{2}+12 x+1 \leq 0$
d) $5 x^{2}+x+1 \geq 0$.
Xét dấu tam thức bậc hai $f(x)=a x^2+b x+c$
Bước 1: Tính $\Delta=b^2-4 a c$
Bước 2:
– Nếu $\Delta0$ thì $f(x)$ có 2 nghiệm là x_1; x_2 (x_1 \lt x_2). Ta lập bảng xét dấu:

a) Tam thức $f(x)=x^2-1$ có $\Delta=4>0$ nên $\mathrm{f}(\mathrm{x})$ có 2 nghiệm phân biệt $x_1=-1; x_2=1$
Mặt khác $a=1>0$, do đó ta có bảng xét dấu:

Mặt khác $a=1>0$, do đó ta có bảng xét dấu:
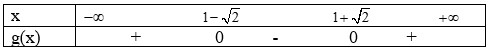
Mặt khác $a=-3<0$, do đó ta có bảng xét dấu:

d) Tam thức $k(x)=5 x^2+x+1$ có $\Delta=-190$ nên $\mathrm{k}(\mathrm{x}$ ) luôn dương ( cùng dấu với a) với mọi x, tức là $5 x^2+x+1>0$ với mọi $x \in \mathbb{R}$. Suy ra bất phương trình có vô số nghiệm
Bài tập 6.17 trang 24
$$x^2+(m+1) x+2 m+3$$
Để tam thức bậc hai $a x^2+b x+c>0$ với mọi $x \in \mathbb{R}$ thì:
$a>0$ và $\Delta<0$
Để tam thức bậc hai $x^2+(m+1) x+2 m+3>0$ với mọi $x \in \mathbb{R}$
Ta có: $\mathrm{a}=1>0$ nên $\Delta<0$
$$\begin{aligned}& \Leftrightarrow(m+1)^2-4 \cdot(2 m+3)<0 \\& \Leftrightarrow m^2+2 m+1-8 m-12<0 \\& \Leftrightarrow m^2-6 m-110$ nên $\mathrm{f}(\mathrm{x})$ có 2 nghiệm phân biệt $m_1=3+\sqrt{20} ; m_2=3-\sqrt{20}$
Khi đó:
$3+\sqrt{20}\lt m \lt 3-\sqrt{20}$
Vậy $m \in(3-2 \sqrt{5} ; 3+2 \sqrt{5})$ thì tam thức bậc hai đã cho luôn dương với mọi $x \in \mathbb{R}$
Bài tập 6.18 trang 24
Tìm hàm tính độ cao so với mặt đất của vật $h(t)$,
Tìm khoảng thời gian $\mathrm{t}$ để $320-h(t) \leq 100$, bài toán đưa về xét dấu tam thức $f(t)=a t^2+b t+c$
Bước 1: Tính $\Delta=b^2-4 a c$
Bước 2:
– Nếu $\Delta0$ thì $f(t)$ có 2 nghiệm là x_1; x_2 (x_1 \lt x_2).
Ta lập bảng xét dấu.

Quãng đường vật rơi được sau $\mathrm{t}(\mathrm{s})$ là: $h(t)=20 t+\frac{1}{2} .9,8 . t^2=4,9 . t^2+20 t$
Để vật cách mặt đất không quá $100 \mathrm{~m}$ thì:
$$320-h(t) \leq 100 \Leftrightarrow h(t) \geq 220 \Leftrightarrow 4,9 t^2+20 t-220 \geq 0$$
Tam thức $f(t)=4,9 t^2+20 t-220$ có $\Delta^{\prime}=1178>0$ nên $f(t)$ có 2 nghiệm phân biệt $t_1=\frac{-10-\sqrt{1} 178}{4,9} ; t_2=\frac{-10+\sqrt{1} 178}{4,9}(\mathrm{t}>0)$
Mặt khác $a=1>0$ nên ta có bảng xét dấu:

Vậy sau ít nhất khoảng $5 s$ thì vật đó cách mặt đất không quá $100 \mathrm{~m}$
Bài tập 6.19 trang 24
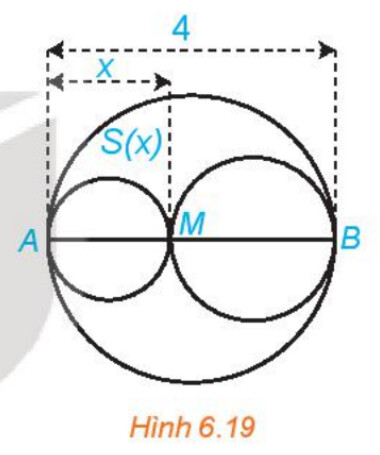
Bước 1: Tính diện tích hình tròn đường kính $AB, AM, MB$ theo $x$
Bước 2: Tính diện tích phần hình phằng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ theo $x$
Bước 3: Lập bất phương trình từ dữ kiện bài toán
Ta có: $\mathrm{AM}<\mathrm{AB}$ nên $0<x0$ nên $\mathrm{f}(\mathrm{x})$ có 2 nghiệm phân biệt $x_1=\frac{6-2 \sqrt{3}}{3} ; x_2=\frac{6+2 \sqrt{3}}{3}$
Mặt khác $a=3>0$, do đó ta có bảng xét dấu:
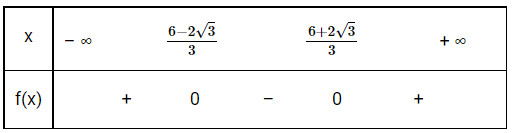
Mà $0<\mathrm{x}<4$ nên $x \in\left(-\infty ; \frac{6-2 \sqrt{3}}{3}\right] \cup\left[\frac{6+2 \sqrt{3}}{3} ;+\infty\right)$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Dấu của tam thức bậc hai Chương Hàm số, đồ thị và ứng dụng Toán 10 Kết nối tri thức tập 2 ở các trang 19, 20, 21, 22, 23, 24. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!





