Giải SGK bài 9 chương 5 trang 61, 62, 63, 64, 65, 66 Toán 6 Cánh diều Tập 2
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Tỉ số và tỉ số phần trăm. Các bài tập sau đây thuộc bài 9 chương 5 – Phân số và số thập phân trang 61, 62, 63, 64, 65, 66 sách Cánh Diều tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài Tỉ số và tỉ số phần trăm
Dưới đây là phương pháp và bài giải chi tiết cho các câu hỏi, hoạt động khám phá, thực hành cùng phần luyện tập ở các trang 61, 62, 63, 64, 65 trong bài Tỉ số và tỉ số phần trăm. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Câu hỏi khởi động trang 61
$\pi$ từ giữa thế kỉ XVIII. Số $\pi$ thể hiện mối liên hệ đặc biệt giữa độ dài của một đường tròn với độ dài đường kính của đường tròn đó. Mối liên hệ đặc biệt giữa độ dài của một đường tròn với độ dài đường kính của đường tròn đó là gì?
Độ dài đường tròn= Chu vi đường tròn= $\pi.d$, với d là đường kính của đường tròn đó
Tỉ lệ giữa độ dài của một đường tròn với độ dài đường kính của đường tròn đó là:
$\pi.d :d=\pi$
Vậy tỉ lệ độ dài của một đường tròn với độ dài đường kính của đường tròn đó luôn bằng $\pi$
Luyện tập vận dụng 1 trang 62
b) Trong các tỉ số đã viết, tỉ số nào là phân số?
Tỉ số của số a và số b phải được viết theo đúng thứ tự là $\frac{a}{b}$ hoặc a : b.
Phân số có dạng $\frac{a}{b}(a, b \in Z, b \neq 0)$
Lời giải chi tiết
a) $\frac{-5}{-7} ; \frac{23,7}{89,6} ; 4: \frac{3}{7}$
b) Trong các tỉ số trên có $\frac{-5}{-7}$ là phân số.
Luyện tập vận dụng 2 trang 63
Tính tỉ số của vận tốc ánh sáng và vận tốc âm thanh.
Tỉ số của số a và số b phải được viết theo đúng thứ tự là $\frac{a}{b}$ hoặc a : b.
Ta có: Vận tốc chuyển động của ánh sáng là: $300000 \mathrm{~km} / \mathrm{s}=300000000 \mathrm{~m} / \mathrm{s}$
Vận tốc chuyển động của âm thanh là: $343,2 \mathrm{~m} / \mathrm{s}$
Vậy tỉ số của vận tốc ánh sáng và vận tốc âm thanh là: $\frac{300000000}{343,2} \approx 874125,9$
Hoạt động 3 trang 63
Tỉ số phần trăm của a và b là $\frac{a}{b}.100\%$
Tỉ số phần trăm của 3 và 5 là:
$\frac{3}{5}.100\%=60\%$
Luyện tập vận dụng 3 trang 63
Tỉ số phần trăm của a và b là $\frac{a}{b}.100\%$
Tỉ số phần trăm của a và b với b = 10 là:
$\frac{a}{10}.100\%=\frac{10}{a}\%$
Tỉ số phần trăm của a và b với b = 100 là:
$\frac{a}{100}.100\%=a\%$
Tỉ số phần trăm của a và b với b = 1000 là:
$\frac{a}{1000}.100\%=\frac{a}{10}\%$
Luyện tập vận dụng 4 trang 64
Khi tính tỉ số phần trăm của a và b mà phải làm tròn số thập phân thì ta làm theo cách thứ hai đã nêu ở trên: Nhân a với 100 rồi chia cho b và làm tròn số thập phân nhận được.
Tỉ số phần trăm của 12 và 35 là:
$\frac{12.100}{35} \%\approx34,3\%$
Hoạt động 4 trang 64
Vận tốc của xe ô tô tải bằng bao nhiêu phần trăm vận tốc của xe ô tô con?
Tỉ số phần trăm của đại lượng thứ nhất có số đo (đại lượng) a và đại lượng thứ hai có số đo (đại lượng) b là:
$\frac{a.100}{b}\%$
Tỉ số vận tốc xe ô tô tải và xe ô tô con là:
$\frac{45.100}{60}\%=75\%$
Luyện tập vận dụng 5 trang 65
Tỉ số phần trăm của đại lượng thứ nhất có số đo (đại lượng) a và đại lượng thứ hai có số đo (đại lượng) b là:
$\frac{a.100}{b}\%$
Tỉ số phần trăm của dân số nữ so với dân số cả nước là:
$\frac{48 327 923}{96 208 984}\%=50,2\%$
Bài tập SGK bài Tỉ số và tỉ số phần trăm
Tiếp theo là các bài tập SGK trang 65, 66 bài Tỉ số và tỉ số phần trăm, thuộc chương 5 – Phân số và số thập phân Toán 6 Cánh diều tập 2. Cùng HocThatGioi giải ngay nhé!
Bài tập 1 trang 65
a) $\frac{4}{3} \mathrm{~m}$ và $75 \mathrm{~cm}$
b) $\frac{7}{10}$ giờ và 25 phút;
c) $10 \mathrm{~kg}$ và 10 tạ.
Tỉ số của số a và số b là $\frac{a}{b}$ hoặc $a$ : b.
Chú ý: Đưa các đại lượng về cùng đơn vị đo.
a) Đổi $75 \mathrm{~cm}=\frac{75}{100}=\frac{3}{4} \mathrm{~m}$
$\Rightarrow$ Tỉ số: $\frac{4}{3}: \frac{3}{4}=\frac{4}{3} \cdot \frac{4}{3}=\frac{16}{9}$.
b) Đổi 25 phút $=\frac{25}{60}=\frac{5}{12}$ giờ
=> Tỉ số: $\frac{7}{10}: \frac{5}{12}=\frac{7}{10} \cdot \frac{12}{5}=\frac{42}{25}$
c) Đổi $10 \mathrm{tạ}=1000 \mathrm{~kg}$
=> Tỉ số: $10: 1000=\frac{1}{100}$
Bài tập 2 trang 65
a) 16 và 75;
b) 6,55 và 8,1.
Tỉ số phần trăm của a và b là $\frac{a}{b}.100\%$
Tỉ số phần trăm của 16 và 75 là:
$\frac{16}{75}.100\%=21,3\%$
Tỉ số phần trăm của 6,55 và 8,1 là:
$\frac{6,55}{8,1}.100\%=80,9\%$
Bài tập 3 trang 65
a) Hỏi tháng nào doanh nghiệp bán được nhiều xi măng nhất? Ít xi măng nhất?
b) Tính tỉ số phần trăm của số lượng xi măng bán ra trong tháng 12 và tổng số lượng xi măng bán ra trong cả bốn tháng (làm tròn kết quả đến hàng đơn vị). ?
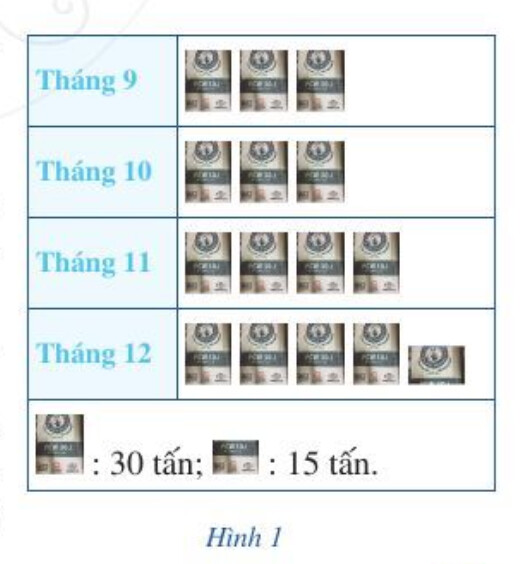
a) Quan sát biểu đồ để xác định tháng nào doanh nghiệp bán được nhiều xi măng nhất? Ít xi măng nhất?
b) – Tính số lượng xi măng bán ra trong tháng 12
– Tính tổng số lượng xi măng bán ra trong cả bốn tháng.
=> Tỉ số phần trăm của số lượng xi măng bán ra trong tháng 12 và tổng số lượng xi măng bán ra trong cả bốn tháng.
a) Tháng 12 doanh nghiệp bán được nhiều xi măng nhất
Tháng 9 và tháng 10 doanh nghiệp bán được ít xi măng nhất
b) Lượng xi măng bán ra trong tháng 12 là:
$30.4 + 15 = 135$ (tấn)
Lượng xi măng bán ra trong cả bốn tháng là:
$3.30+3.30+4.30+135=435$ (tấn)
Tỉ số phần trăm của số lượng xi măng bán ra trong tháng 12 và tổng lượng xi măng bán ra trong cả bốn tháng là:
$\frac{135}{435}.100\%=31\%$
Bài tập 4 trang 66
a) Bạn Châu đọc sách nhiều nhất vào ngày nào?
b) Tính tỉ số phần trăm (làm tròn đến hàng phẩn mười) của tổng số giờ đọc sách của bạn Châu trong ba ngày cuối tuần so vởi tổng số giờ trong ba ngày cuối tuần. Theo em, bạn Châu có nên dành nhiều thời gian để đọc sách hơn không?
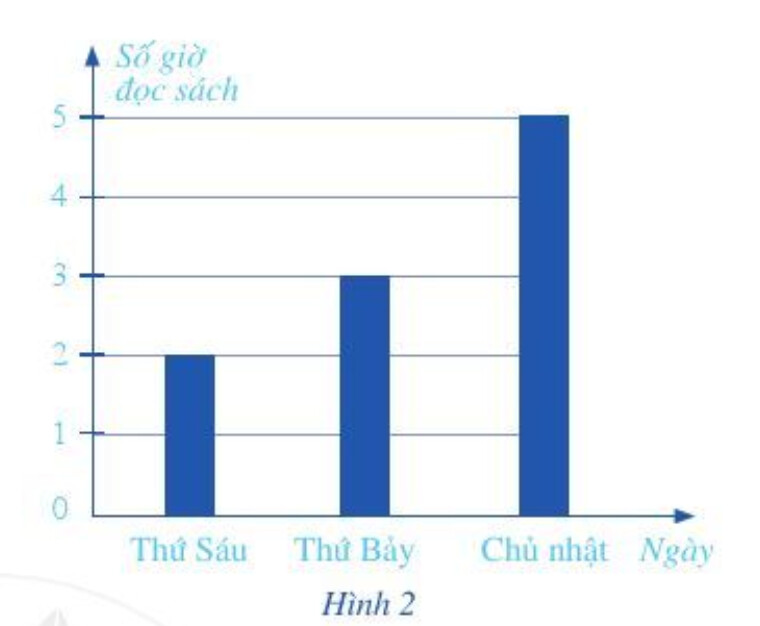
a) Châu đọc sách nhiều nhất vào ngày có cột số giờ đọc sách cao nhất.
b)
– Tính tổng số giờ đọc sách của bạn Châu trong ba ngày cuối tuần
– Tính tổng số giờ trong ba ngày cuối tuần
=> Tỉ số phần trăm của tổng số giờ đọc sách của bạn Châu trong ba ngày cuối tuần so với tổng số giờ trong ba ngày cuối tuần
a) Theo biểu đồ cột ở Hình 2, ta thấy cột cao nhất tương ứng với ngày chủ nhật bạn Châu dành nhiều thời gian đọc sách nhất.
b) Mỗi ngày có 24 giờ nên tổng số giờ trong ba ngày cuối tuần là: $24.3 = 72$ (giờ).
Tổng số giờ đọc sách trong ba ngày cuối tuần là: $2 + 3 + 5 = 10$ (giờ).
Tỉ số phần trăm của tổng số giờ đọc sách của bạn Châu trong ba ngày cuối tuần với tổng số giờ trong ba ngày cuối tuần là:
$\frac{10}{72}.100\%=13,9\%$
Một ngày chỉ nên dành khoảng 1 đến 3 tiếng để đọc sách để não bộ tiếp nhận và xử lý thông tin tốt hơn nên bạn Châu không nên dành nhiều thời gian để đọc sách nữa mà thay vào đó nên chọn các hoạt động thể dục, thể thao tăng cường sức khỏe, các hoạt động học tập, vui chơi, giải trí khác.
Bài tập 5 trang 66
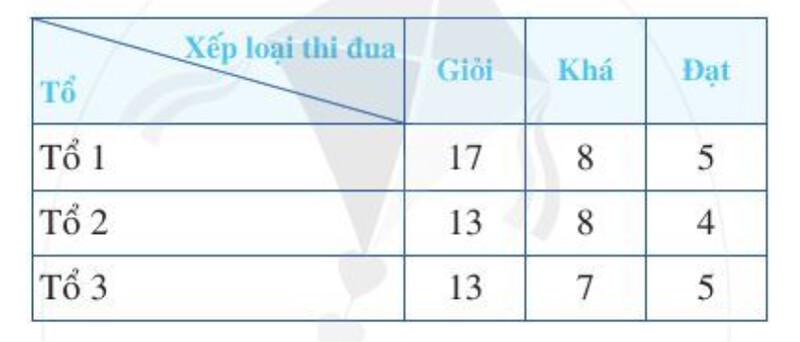
a) Mỗi tổ lao động có bao nhiêu người?
b) Đội trưởng thông báo rằng tỉ số phần trăm của số lao động giỏi ở cả đội so với số người ở cả đội là lớn hơn 53\%. Thông báo đó của đội trưởng có đúng không?
a) Số lao động mỗi tổ = Số lao động giỏi + số lao động khá + số lao động đạt (của mỗi tổ)
b)
– Tính số lao động giỏi ở cả đội.
– Tính số người ở cả đội.
=> Tỉ số phần trăm của số lao động giỏi ở cả đội so với số người ở cả đội.
a) Số người của tổ 1 là: 17 + 8 + 5 = 30 (người).
Số người của tổ 2 là: 13 + 8 + 4 = 25 (người).
Số người của tổ 3 là: 13 + 7 + 5 = 25 (người).
Vậy số người của tổ 1, tổ 2 và tổ 3 lần lượt là: 30 người, 25 người, 25 người.
b) Tổng số người của cả đội là: 30 + 25 + 25 = 80 (người).
Số lao động giỏi của cả đội là: 17 + 13 + 13 = 43 (người).
Tỉ số phần trăm của số lao động giỏi của cả đội so với số người cả đội là:
$\frac{43}{80}.100\%=54,75\%\gt53\%$
Vậy thông báo của đội trưởng là chính xác
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 8 Tỉ số và tỉ số phần trăm chương 5 sách Toán 6 Cánh Diều tập 2 ở các trang 61, 62, 63, 64, 65, 66. Chúc các bạn có một buổi học thật thú vị và bổ ích!





