Giải SGK bài tập cuối chương IX Toán 10 Kết nối tri thức Tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi trắc nghiệm cũng như bài tập tự luận trong bài tập cuối chương IX. Đây là Bài tập cuối chương IX trang 88, 89 sách Toán 10 Kết nối tri thức tập 2. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi trắc nghiệm trong SGK của bài tập cuối chương IX
Sau khi đã học lý thuyết và giải các bài tập ở Chương Tính xác suất theo định nghĩa cổ điển. Cùng HocThatGioi giải chi tiết phần câu hỏi trắc nghiệm ở trang 88 trong bài tập cuối chương IX ngay sau đây nhé!
Bài 9.13 trang 88
A. Lấy được viên bi xanh.
B. Lấy được viên bi vàng hoặc bi trắng
C. Lấy được viên bi trắng.
D. Lấy được viên bi vàng hoặc bi trắng hoặc bi xanh.
E và $\bar{E}$ là hai biến cố đối khi và chỉ khi $E \cup \bar{E}=\Omega$ và $E \cap \bar{E}=\emptyset$
Chọn $D$.
Bài 9.14 trang 88
A. $\frac{1}{30}$
B. $\frac{1}{5}$
C. $\frac{1}{3}$
D. $\frac{2}{5}$
Các số chia hết cho 5 là các số có chữ số tận cùng là 0 hoặc 5.
Số phần tử của không gian mẫu làn $(\Omega)=30$.
Gọi $E$ là biến cố: “Số trên thẻ được rút ra là số chia hết cho 5 “
Ta có: $E=\{5 ; 10 ; 15 ; 20 ; 25 ; 30\}$
$\Rightarrow n(E)=6$
Vậy xác suất của biến cố $E$ là $P(E)=\frac{n(E)}{n(\Omega)}=\frac{1}{5}$.
$=>$ Chọn $B$
Bài 9.15 trang 88
A. $\frac{1}{7}$
B. $\frac{1}{6}$
C. $\frac{1}{8}$
D. $\frac{2}{9}$
Sử dụng công thức xác suất cổ điển $P(E)=\frac{n(E)}{n(\Omega)}$.
Số phần tử của không gian mẫu là $n(\Omega)=36$
Gọi $E$ là biến cố $E$={(1,1); (1 ; 2); (1,3); (2 ; 1); (2 ; 2); (3,1)}
Suy ra $n(E)=6$
Vậy $P(E)=\frac{6}{36}=\frac{1}{6}$.
$=>$ Chọn $B$
Bài 9.16 trang 88
A. $\frac{4}{7}$
B. $\frac{2}{7}$
C. $\frac{1}{6}$
D. $\frac{2}{21}$
Sử dụng công thức xác suất cổ điển $P(E)=\frac{n(E)}{n(\Omega)}$.
Cách chọn 2 bạn từ 10 bạn là $C_{10}^2 \Rightarrow n(\Omega)=C_{10}^2=21$
Gọi $A$ là biến cố: “Hai bạn được chọn có một bạn nam và một bạn nữ”.
Cách chọn một bạn nam là: $3$ cách chọn
Cách chọn một bạn nữ là: $4$ cách chọn
Theo quy tắc nhân ta có $n(A)=3.4=12$
Vậy xác suất của biến cố $\mathrm{A}$ là $P(A)=\frac{n(A)}{n(\Omega)}=\frac{12}{21}=\frac{4}{7}$.
$=>$ Chọn A
Trả lời câu hỏi tự luận trong SGK của bài tập cuối chương IX
Phần tiếp theo sẽ cung cấp cho các bạn phương pháp cùng lời giải trong phần câu hỏi tự luận trang 88, 89 cực kỳ dễ hiểu và chi tiết. Cùng HocThatGioi rèn luyện và nâng cao kỹ năng giải quyết các vấn đề thực tế thông qua các phương pháp, công thức toán học từ Chương Tính xác suất theo định nghĩa cổ điển.
Bài 9.17 trang 88
a) Mô tả không gian mẫu.
b) Mỗi biến cố sau là tập con nào của không gian mẫu?
A: “Rút ra được thẻ màu đỏ hoặc màu vàng”
B: “Rút ra được thẻ mang số hoặc là 2 hoặc là 3”
Kí hiệu $X_1, X_2, \ldots, X_7$ là bảy thẻ màu xanh, $D_1, D_2, \ldots, D_5$ là 5 thẻ màu đỏ và $V_1, V_2$ là hai thẻ màu vàng.
a) Kí hiệu $X_1, X_2, \ldots, X_7$ là bảy thẻ màu xanh, $D_1, D_2, \ldots, D_5$ là 5 thẻ màu đỏ và $V_1, V_2$ là hai thẻ màu vàng.
Ta có không gian mẫu là:
$\Omega $= {X1, X2,…, X7, D1, D2,…, D5, V1, V2}
b) Ta có:
$A=\left\{D_1, D_2, D_3, D_4, D_5, V_1, V_2\right\}$
$B=\left\{X_2, X_3, D_2, D_3, V_2\right\}$.
Bài 9.18 trang 88
Số phần tử của không gian mẫu là $n(\Omega)=5.5=25$.
Gọi $E$ là biến cố: “thẻ rút ra từ hộp II mang số lớn hơn số trên thẻ rút ra từ hộp I”
$E$= {(4,5); (3,4); (3,5); (2,3); (2,4); (2,5); (1,2); (1 ; 3); (1,4); (1,5)}
Suy ra $n(E)=10$
Vậy $P(E)=\frac{n(E)}{n(\Omega)}=\frac{2}{5}$
Bài 9.19 trang 88
a) Tổng số chấm trên hai con xúc xắc bằng 8.
b) Tổng số chấm trên hai con xúc xắc nhỏ hơn 8.
Số phần tử của không gian mẫu là $n(\Omega)=36$.
a) Gọi A là biến cố: “Tổng số chấm trên hai con xúc xắc bằng 8 “
Ta có $A=\{(2,6) ;(3,5) ;(4,4) ;(5,3) ;(6,2)\}$
Suy ra $n(A)=5$
Vậy xác suất của biến cố $\mathrm{A}$ là $P(A)=\frac{n(A)}{n(\Omega)}=\frac{5}{36}$
b) Gọi B là biến cố: “Tổng số chấm trên hai con xúc xắc nhỏ hơn 8”
Gọi C là biến cố: “Tổng số chấm trên hai con xúc xắc lớn hơn 8 “
$C$={(3 ; 6), (4 ; 5), (4 ; 6), (5 ; 4), (5 ; 5), (5 ; 6), (6 ; 3), (6 ; 4), (6 ; 5), (6 ; 6)}
Suy ra $n(C)=10$
Ta có: $n(B)=n(\Omega)-n(A)-n(C)=21$
Vậy xác suất của biến cố $\mathrm{B}$ là $P(B)=\frac{n(B)}{n(\Omega)}=\frac{21}{36}=\frac{7}{12}$.
Bài 9.20 trang 89
a) Vẽ sơ đồ hình cây mô tả không gian mẫu.
b) Tính xác suất của các biến cố:
F: “Trong ba ngày, có đúng một ngày có mưa”;
G: “Trong ba ngày, có ít nhất hai ngày không mưa”.
a) Sơ đồ cây trong đó $B$ là ngày có mưa và $A$ là nhà không mưa.
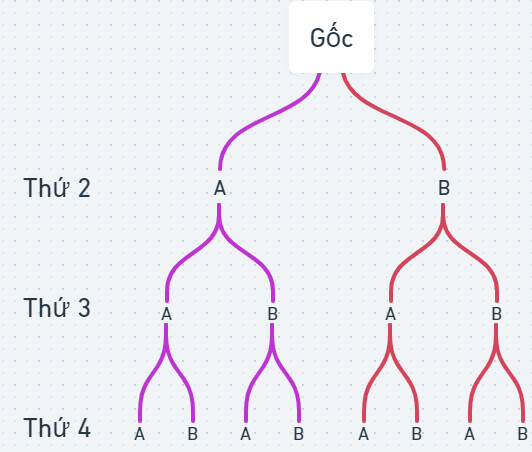
Dựa vào sơ đồ cây ta thấy $n(\Omega)=8$.
b) Ta có $F=\{A A B, A B A, B A A\}$.
Vậy $P(F)=\frac{3}{8}$.
$$G=\{A A B, A B A, B A A, A A A\}$$
Vậy $P(G)=\frac{1}{2} \text {. }$
Bài 9.21 trang 89
a) Vẽ sơ đồ hình cây mô tả không gian mẫu.
b) Tính xác suất để trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa.
a) Kí hiệu $S$ là đồng xu ra mặt sấp và $N$ là đồng xu ra mặt ngửa.
Ta có sơ đồ cây:
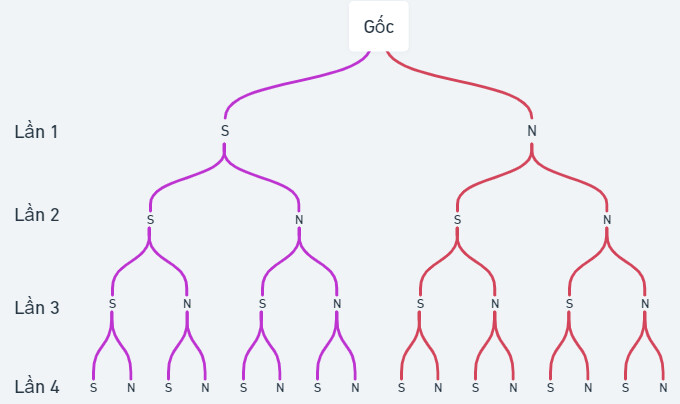
Dựa vào sơ đồ cây ta suy ra $n(\Omega)=16$.
b) Gọi A là biến cố: “gieo đồng xu 4 lần có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa”
Suy ra $A$= {SSNN ; SNSN ; SNNS ; NSSN ; NSNS ; NNSS}.
Suy ra $n(A)=6$.
Vậy $P(A)=\frac{6}{16}=\frac{3}{8}$.
Bài 9.22 trang 89
$\bar{A}$ là biến cố: “Trong 4 viên bi chỉ có toàn bi đỏ hoặc bi xanh”.
Ta có: $(\Omega)=C_{10}^4=210$ và $n(\vec{A})=16$.
Do đó $P(\vec{A})=\frac{16}{210}$
Suy ra $P(A)=1-\frac{16}{240}=\frac{194}{210}=\frac{97}{105}$.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK Bài tập cuối chương Tính xác suất theo định nghĩa cổ điển Toán 10 Kết nối tri thức tập 2 ở các trang 88. 89. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!





