SGK Toán 10 - Kết Nối Tri Thức
Giải SGK bài Mạng xã hội lợi và hại Toán 10 Kết nối tri thức tập 1
Khi đã học xong toàn bộ lý thuyết cũng như thực hành bài tập vận dụng trong SGK Kết nối tri thức tập 1, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Mạng xã hội: lợi và hại trang 96, 97, 98, 99, 100, 101. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Hoạt động 1 trang 97
Hãy dùng phiếu khảo sát theo mẫu trên, tiến hành thu thập dữ liệu với ít nhất 30 phiếu và ghi lại dữ liệu theo mẫu sau:
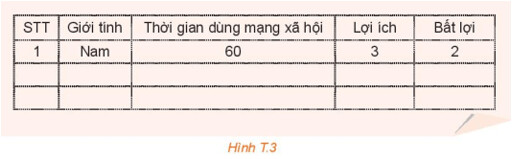

Lời giải chi tiết:
Chẳng hạn: Kết quả khảo sát ở $30$ bạn trong lớp em:
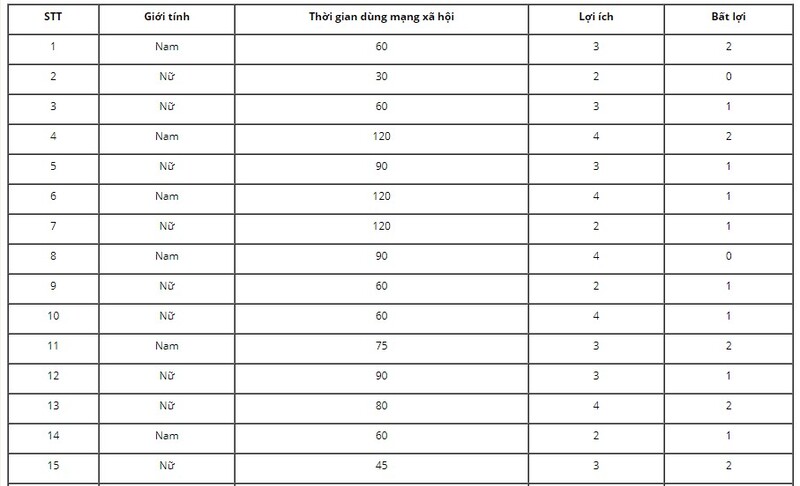
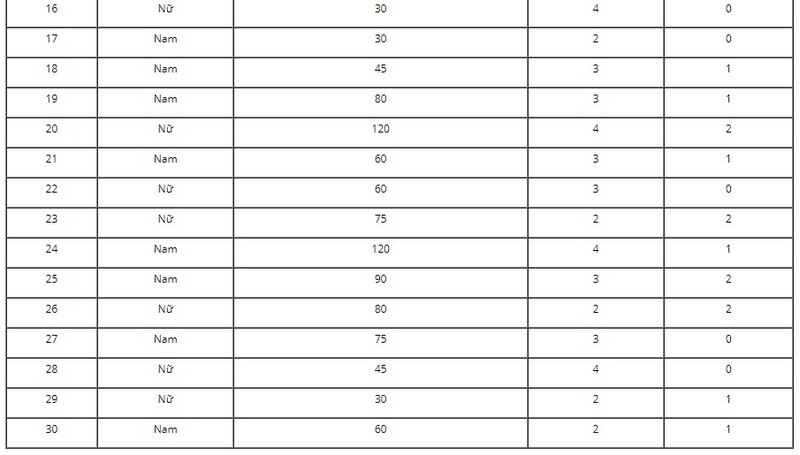
Chẳng hạn: Kết quả khảo sát ở $30$ bạn trong lớp em:


Hoạt động 2 trang 97
Để biết các bạn học sinh tham gia khảo sát đánh giá thế nào về lợi ích và bất lợi của mạng xã hội, hãy thực hiện các yêu cầu sau:
a) Lập bảng tần số của dữ liệu ý kiến về lợi ích/ bất lợi của mạng xã hội theo mẫu sau:

b) Rút ra nhận xét từ bảng tần số thu được.
a) Lập bảng tần số của dữ liệu ý kiến về lợi ích/ bất lợi của mạng xã hội theo mẫu sau:

b) Rút ra nhận xét từ bảng tần số thu được.
Lời giải chi tiết:
a) Bảng tần số của dữ liệu ý kiến về lợi ích của mạng xã hội:

Bảng tần số của dữ liệu ý kiến về bất lợi của mạng xã hội:

b) Nhận xét:
Các HS lớp em đều cảm thấy mạng xã hội mang đến nhiều lợi ích hơn là bất lợi.
Các bất lợi thường gặp là mất thời gian sử dụng.
a) Bảng tần số của dữ liệu ý kiến về lợi ích của mạng xã hội:

Bảng tần số của dữ liệu ý kiến về bất lợi của mạng xã hội:

b) Nhận xét:
Các HS lớp em đều cảm thấy mạng xã hội mang đến nhiều lợi ích hơn là bất lợi.
Các bất lợi thường gặp là mất thời gian sử dụng.
Hoạt động 3 trang 97
Hãy tính một số số đo thống kê mô tả được liệt kê trong Bảng $T.2$ của mẫu số liệu về thời gian sử dụng mạng xã hội:

Dựa trên những số đặc trưng tính được, hãy nêu nhận xét về thời gian sử dụng mạng xã hội của các học sinh được khảo sát.

Dựa trên những số đặc trưng tính được, hãy nêu nhận xét về thời gian sử dụng mạng xã hội của các học sinh được khảo sát.
Phương pháp giải:
Số trung bình $\bar{x}=\frac{x_1+x_2+\ldots+x_{30}}{30}$
Bước 1: Sắp xếp mẫu số thành dãy không giảm $x_1, x_2, \ldots, x_{30}$
Bước 2: Cỡ mẫu $n=30$
Trung vị: $M_e=\frac{1}{2}\left(x_{15}+x_{16}\right)$
$Q_1$ là trung vị của mẫu $x_1, x_2, \ldots, x_{15}$, do đó $Q_1=x_8$
$Q_3$ là trung vị của mẫu $x_{16}, x_{17}, \ldots, x_{30}$, do đó $Q_3=x_{23}$
Mốt là giá trị xuất hiện nhiều lần nhất.
Số trung bình $\bar{x}=\frac{x_1+x_2+\ldots+x_{30}}{30}$
Bước 1: Sắp xếp mẫu số thành dãy không giảm $x_1, x_2, \ldots, x_{30}$
Bước 2: Cỡ mẫu $n=30$
Trung vị: $M_e=\frac{1}{2}\left(x_{15}+x_{16}\right)$
$Q_1$ là trung vị của mẫu $x_1, x_2, \ldots, x_{15}$, do đó $Q_1=x_8$
$Q_3$ là trung vị của mẫu $x_{16}, x_{17}, \ldots, x_{30}$, do đó $Q_3=x_{23}$
Mốt là giá trị xuất hiện nhiều lần nhất.
Lời giải chi tiết:

Cụ thể:
Số trung bình $\frac{60+30+\ldots+60}{30}=72$
Bước 1: Sắp xếp mẫu số thành dãy không giảm ta được: 30, 30, 30, 30, 45, 45, 45, 60, 60, 60, 60, 60, 60, 60, 60, 75, 75, 75, 80, 80, 80, 90, 90, 90, 90, 120, 120, 120, 120, 120.
Bước 2: Cỡ mẫu $n=30$
Trung vị: $M_e=\frac{1}{2}(60+75)=67,5$
$$\begin{aligned}& Q_1=x_8=60 \\& Q_3=x_{23}=90\end{aligned}$$
Nhận xét:
+) Trung bình mỗi bạn sử dụng mạng xã hội khoảng 72 phút/ ngày.
†) Sự chênh lệch thời gian sử dụng giữa các bạn là khá lớn.

Cụ thể:
Số trung bình $\frac{60+30+\ldots+60}{30}=72$
Bước 1: Sắp xếp mẫu số thành dãy không giảm ta được: 30, 30, 30, 30, 45, 45, 45, 60, 60, 60, 60, 60, 60, 60, 60, 75, 75, 75, 80, 80, 80, 90, 90, 90, 90, 120, 120, 120, 120, 120.
Bước 2: Cỡ mẫu $n=30$
Trung vị: $M_e=\frac{1}{2}(60+75)=67,5$
$$\begin{aligned}& Q_1=x_8=60 \\& Q_3=x_{23}=90\end{aligned}$$
Nhận xét:
+) Trung bình mỗi bạn sử dụng mạng xã hội khoảng 72 phút/ ngày.
†) Sự chênh lệch thời gian sử dụng giữa các bạn là khá lớn.
Hoạt động 4 trang 97
a) Hãy tính số trung bình, trung vị, tứ phân vị của thời gian sử dụng mạng xã hội trên hai nhóm học sinh nữa và học sinh năm để so sánh thời gian sử dụng mạng xã hội của hai nhóm.

b) Hãy tính một vài số đo độ phân tán để so sánh sự biến động của thời gian sử dụng mạng xã hội của hai nhóm học sinh.


b) Hãy tính một vài số đo độ phân tán để so sánh sự biến động của thời gian sử dụng mạng xã hội của hai nhóm học sinh.

Phương pháp giải:
Số trung bình $\bar{x}=\frac{x_1+x_2+\ldots+x_{30}}{30}$
Bước 1: Sắp xếp mẫu số thành dãy không giảm $x_1, x_2, \ldots, x_{30}$
Bước 2: Cỡ mẫu $\mathrm{n}=30$
Trung vị: $M_e=\frac{1}{2}\left(x_{15}+x_{16}\right)$
$Q_1$ là trung vị của mẫu $x_1, x_2, \ldots, x_{15}$, do đó $Q_1=x_8$
$Q_3$ là trung vị của mẫu $x_{16}, x_{17}, \ldots, x_{30}$, do đó $Q_3=x_{23}$
Số trung bình $\bar{x}=\frac{x_1+x_2+\ldots+x_{30}}{30}$
Bước 1: Sắp xếp mẫu số thành dãy không giảm $x_1, x_2, \ldots, x_{30}$
Bước 2: Cỡ mẫu $\mathrm{n}=30$
Trung vị: $M_e=\frac{1}{2}\left(x_{15}+x_{16}\right)$
$Q_1$ là trung vị của mẫu $x_1, x_2, \ldots, x_{15}$, do đó $Q_1=x_8$
$Q_3$ là trung vị của mẫu $x_{16}, x_{17}, \ldots, x_{30}$, do đó $Q_3=x_{23}$
Lời giải chi tiết:
a)
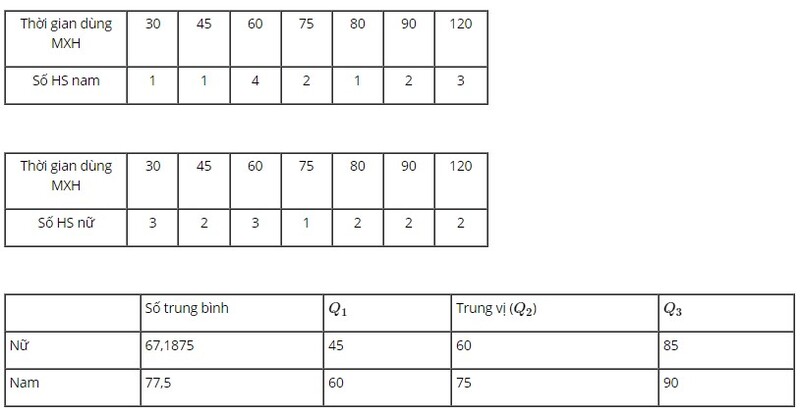
– Số trung bình: các HS nam sử dụng mạng xã hội nhiều hơn so với HS nữ
– Trung vị: các HS nam sử dụng mạng xã hội nhiều hơn so với HS nữ
– Tứ phân vị: thời gian sử dụng phân bố đồng đều ở cả năm và nữ.
b)

Theo kết quả trên: Thời gian sử dụng mạng xã hội của các học sinh nữ có nhiều biến động hơn (một chút) so với các học sinh nam.
a)

– Số trung bình: các HS nam sử dụng mạng xã hội nhiều hơn so với HS nữ
– Trung vị: các HS nam sử dụng mạng xã hội nhiều hơn so với HS nữ
– Tứ phân vị: thời gian sử dụng phân bố đồng đều ở cả năm và nữ.
b)

Theo kết quả trên: Thời gian sử dụng mạng xã hội của các học sinh nữ có nhiều biến động hơn (một chút) so với các học sinh nam.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Mạng xã hội: lợi và hại thuộc phần Hoạt động thực hành trải nghiệm Toán 10 Kết nối tri thức tập 1 ở các trang 96, 97, 98, 99, 100, 101. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!





