Giải SGK bài 13 trang 63,67 Toán 7 Kết nối tri thức tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi, hoạt động, vận dụng,luyện tập và bài tập trong bài Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác. Các bài tập sau đây thuộc bài 13 chương 4 trang 63, 64, 65, 67 SGK Toán 7 Kết nối tri thức. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK trang 63, 64, 65, 66, 67 Toán 7 Kết nối tri thức tập 1
Các câu hỏi, hoạt động, vận dụng,luyện tập ở các trang 63, 64, 65, 66, 67 này sẽ giúp các bạn đi vào bài học tìm hiểu các kiến thức về bài học một cách trơn tru và dễ hiểu hơn rất nhiều đấy! Cùng xem lời giải của HocThatGioi nhé!
HĐ1 trang 63
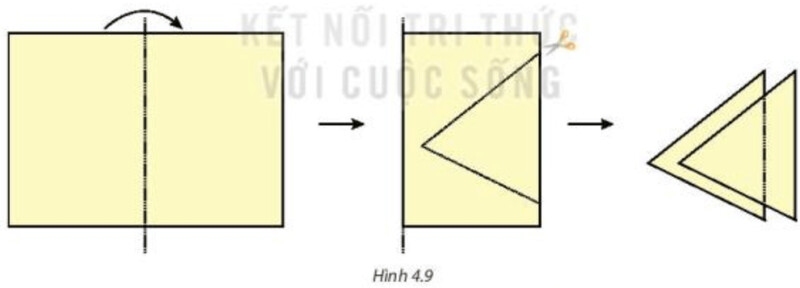
Phần được cắt ra là hai tam giác “chồng khít” lên nhau.
Theo em:
– Các cạnh tương ứng có bằng nhau không?
– Các góc tương ứng có bằng nhau không?
– Các cạnh tương ứng của hai tam giác bằng nhau.
– Các góc tương ứng của hai tam giác bằng nhau.
Câu hỏi trang 64
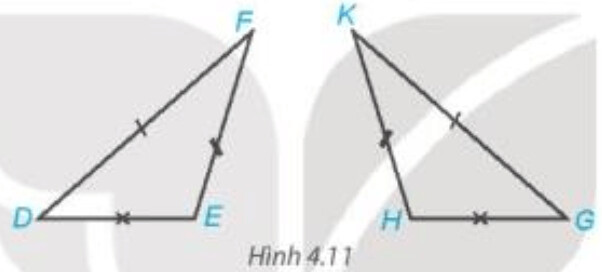
Các cặp cạnh tương ứng: $\mathrm{FE}=\mathrm{KH}, \mathrm{ED}=\mathrm{HG}, \mathrm{DF}=\mathrm{GK}$.
Các cặp góc tương ứng: $\widehat{F}=\widehat{K}, \widehat{E}=\widehat{H}, \widehat{D}=\widehat{G}$.
Kí hiệu bằng nhau của cặp tam giác là: $\triangle D E F=\Delta G H K$.
Luyện tập 1 trang 65
Hãy tính độ dài đoạn thẳng $EF$ và số đo góc $EDF$.
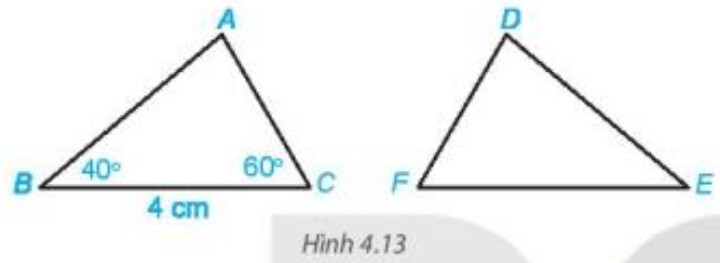
Xét tam giác $A B C$ có $\widehat{A}+\widehat{B}+\widehat{C}=180^{\circ}$.
Do đó $\widehat{A}=180^{\circ}-\widehat{B}-\widehat{C}= 180^{\circ}-60^{\circ}-40^{\circ} =80^{\circ}$.
Do tam giác $A B C$ bằng tam giác $D E F$ nên $E F=B C$ (2 cạnh tương ứng) và $\widehat{E D F}=\widehat{B A C}$ (2 góc tương ứng).
Do đó $\mathrm{EF}=4 \mathrm{~cm}$ và $\widehat{E \mathrm{DF}}=80^{\circ}$.
Vậy $\mathrm{EF}=4 \mathrm{~cm}$ và $\widehat{E D F}=80^{\circ}$.
HĐ2 trang 65
– Dùng thước thẳng có vạch chia vẽ đoạn thẳng $BC = 6 cm$.
– Vẽ cung tròn tâm $B$ bán kính $5 cm$ và cung tròn tâm $C$ bán kính $4 cm$ sao cho hai cung tròn cắt nhau tại điểm $A$ (H.4.14).
– Vẽ các đoạn thẳng $AB, AC$ ta được tam giác $ABC$.
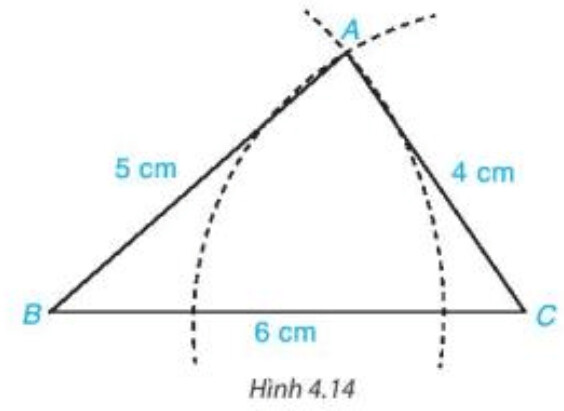
Bước 1. Vẽ đoạn thẳng $BC = 6 cm$.

Bước 2. Vẽ cung tròn tâm $B$ bán kính $5 cm$ và cung tròn tâm $C$ bán kính $4 cm$ sao cho hai cung tròn cắt nhau tại điểm $A$.
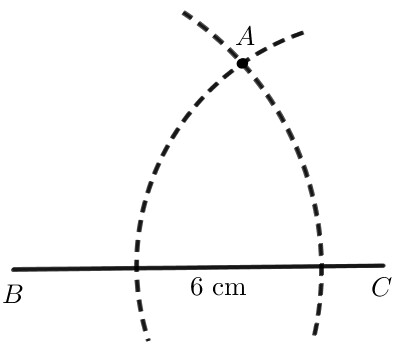
Bước 3. Vẽ các đoạn thẳng $AB, AC$ ta được tam giác $ABC$.
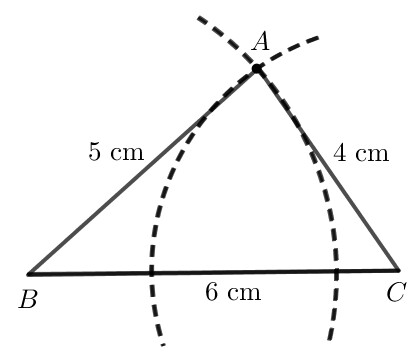
HĐ3 trang 66
– Dùng thước đo góc kiểm tra xem các góc tương ứng của hai tam giác $ABC$ và $A^{\prime} B^{\prime} C^{\prime}$ có bằng nhau không.
– Hai tam giác $\mathrm{ABC}$ và $A^{\prime} B^{\prime} C^{\prime}$ có bằng nhau không?
Vẽ tam giác $A’B’C’$ tương tự như trên.
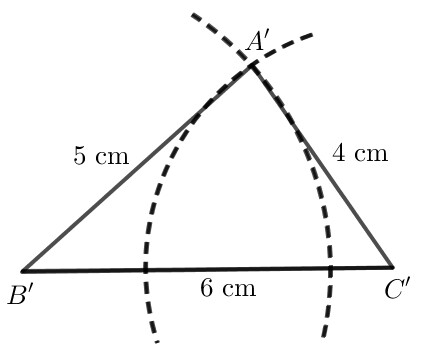
Sử dụng thước đo góc, ta có:
$\widehat{A}=\widehat{A^{\prime}} \approx 82,8^{\circ} ; \widehat{B}=\widehat{B^{\prime}} \approx 41,4^{\circ} ; \widehat{C}=\widehat{C^{\prime}} \approx 55,8^{\circ} $
Các góc tương ứng của hai tam giác $\mathrm{ABC}$ và $A^{\prime} B^{\prime} C^{\prime}$ bằng nhau.
– Hai tam giác $A B C$ và $A^{\prime} B^{\prime} C^{\prime}$ có:
$A B=A^{\prime} B^{\prime}, B C=B^{\prime} C^{\prime}, C A=C^{\prime} A^{\prime}$ (theo giả thiết).
$\widehat{A}=\widehat{A^{\prime}}, \widehat{B}=\widehat{B^{\prime}}, \widehat{C}=\widehat{C^{\prime}}$ (chứng minh trên).
Vậy hai tam giác $A B C$ và $A^{\prime} B^{\prime} C^{\prime}$ có các cạnh và các góc tương ứng bằng nhau.
Do đó $\triangle A B C=\Delta A^{\prime} B^{\prime} C^{\prime}$.
Luyện tập 2 trang 66
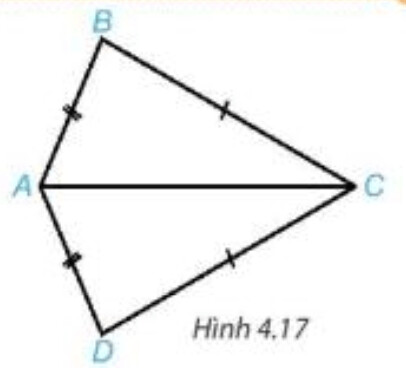
Xét hai tam giác $A B C$ và $A D C$ có:
$A B=A D$ (theo giả thiết)
$B C=D C$ (theo giả thiết)
$AC$ chung
Vậy $\triangle A B C=\Delta A \mathrm{D} C(c-c-c)$.
Vận dụng trang 67
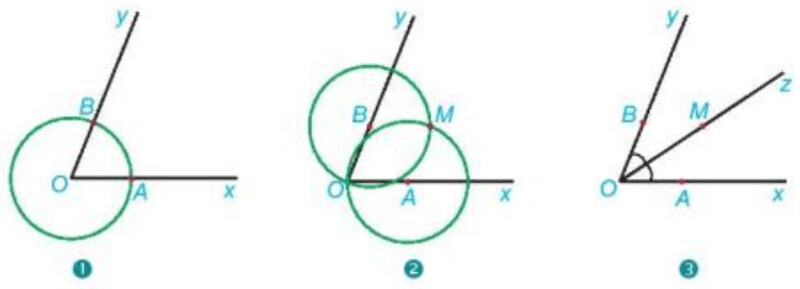
(1) Vẽ đường tròn tâm $\mathrm{O}$ cắt $\mathrm{Ox}$, Oy lần lượt tại $\mathrm{A}$ và $\mathrm{B}$.
(2) Vẽ đường tròn tâm $\mathrm{A}$ bán kính $\mathrm{AO}$ và đường tròn tâm $\mathrm{B}$ bán kính $\mathrm{BO}$. Hai đường tròn cắt nhau tại điểm $\mathrm{M}$ khác điểm $\mathrm{O}$.
(3) Vẽ tia $\mathrm{Oz}$ đi qua $\mathrm{M}$.
Em hãy giải thích vì sao tia $OM$ là tia phân giác của góc $xOy$.
Do $A$ và $B$ thuộc đường tròn tâm $\mathrm{O}$ nên $\mathrm{AO}=\mathrm{BO}$.
Do $\mathrm{M}$ thuộc đường tròn tâm $\mathrm{B}$ bán kính $\mathrm{BO}$ nên $\mathrm{BO}=\mathrm{BM}$.
Do $\mathrm{M}$ thuộc đường tròn tâm $\mathrm{A}$ bán kính $\mathrm{AO}$ nên $\mathrm{AO}=\mathrm{AM}$.
Mà $A O=B O$ nên $A M=B M$.
Xét hai tam giác $O B M$ và $O A M$ có:
$\mathrm{BO}=\mathrm{AO}$ (chứng minh trên).
$\mathrm{BM}=\mathrm{AM}$ (chứng minh trên).
OM chung.
Do đó $\triangle O B M=\triangle O A M(c-c-c)$.
Do đó $\widehat{B O M}=\widehat{A O M}$ (2 góc tương ứng).
Mà $\mathrm{OM}$ nằm giữa hai tia $\mathrm{OA}$ và $\mathrm{OB}$ nên $\mathrm{OM}$ là tia phân giác của $\widehat{A O B}$ hay $\mathrm{OM}$ là tia phân giác của $\widehat{x O y}$.
Vậy $OM$ là tia phân giác của $\widehat{x O y}$.
Giải bài tập SGK trang 67 Toán 7 Kết nối tri thức tập 1
Những bài tập SGK ở cuối bài trang 67 sách Toán 7 kết nối tri thức sẽ giúp các bạn vận dụng những kiến thức vừa học để giải các bài tập từ cơ bản đến nâng cao. Cùng HocThatGioi giải quyết những bài toán này nhé!
Bài 4.4 trang 67
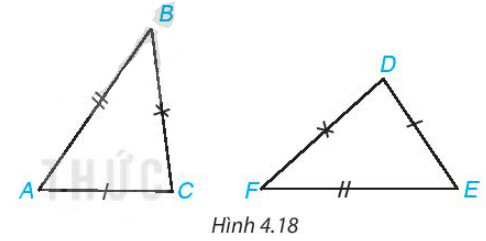
Trong các khẳng định sau, khẳng định nào đúng?
(1) $\triangle A B C=\triangle D E F$;
(2) $\triangle A C B=\triangle E D F$;
(3) $\triangle B A C=\triangle D F E$;
(4) $\triangle C A B=\triangle D E F$.
Quan sát hình, ta thấy $\mathrm{AB}=\mathrm{EF}, \mathrm{BC}=\mathrm{FD}, \mathrm{CA}=\mathrm{DE}$.
Khi đó:
$\triangle A B C=\triangle E F D$ nên khẳng định (1) sai.
$\Delta A C B=\triangle E \mathrm{D} F$ nên khẳng định (2) đúng.
$\Delta B A C=\Delta F \mathrm{ED}$ nên khẳng định (3) sai.
$\triangle C A B=\triangle D E F$ nên khẳng định (4) đúng.
Bài 4.5 trang 67
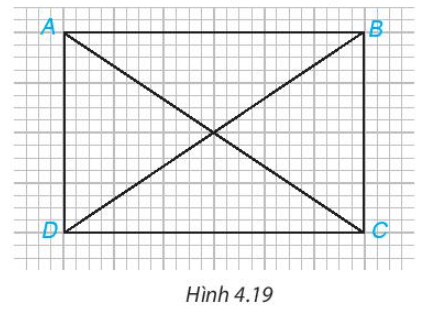
Xét hai tam giác $A B D$ và $C D B$ có:
$A B=C D$ (cùng có độ dài bằng 6 ô vuông).
$A D=B C$ (cùng có độ dài bằng 4 ô vuông).
$BD$ chung.
Do đó $\triangle A B \mathrm{D}=\triangle C \mathrm{D} B(c-c-c)$.
Xét hai tam giác $A C D$ và $C A B$ có:
$A D=B C$ (cùng có độ dài bằng 4 ô vuông).
$\mathrm{CD}=\mathrm{AB}$ (cùng có độ dài bằng 6 ô vuông).
$AC$ chung.
Do đó $\triangle A C \mathrm{D}=\triangle C A B(c-c-c)$.
Vậy hai cặp tam giác bằng nhau là: $\triangle \mathrm{ABD}=\triangle C D B, \triangle A C D=\triangle C A B$
Bài 4.6 trang 67
a) Chứng minh rằng $\triangle A B \mathrm{D}=\triangle C B \mathrm{D}$.
b) Tinh $\widehat{A B C}$.
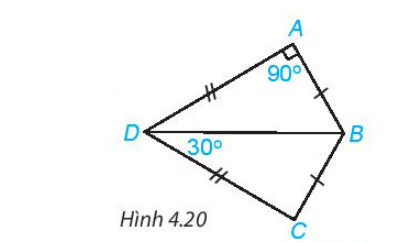
a) Xét hai tam giác $A B D$ và $C B D$ có:
$\mathrm{AB}=\mathrm{BC}$ (theo giả thiết).
$A D=C D$ (theo giả thiết).
$BD$ chung.
Vậy $\triangle A B \mathrm{D}=\triangle C B \mathrm{D}(c-c-c)$.
b) $\mathrm{Do} \Delta A B \mathrm{D}=\triangle C B \mathrm{D}$ nên $\widehat{A \mathrm{D} B}=\widehat{C \mathrm{D} B}$ (2 góc tương ứng).
Do đó $\widehat{A \mathrm{DB}}=30^{\circ}$.
Xét tam giác $\mathrm{ABD}$ vuông tại $\mathrm{A}$ có: $\widehat{A B \mathrm{D}}+\widehat{A \mathrm{DB}}=90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).
Do đó $\widehat{A B \mathrm{D}}=90^{\circ}-\widehat{A \mathrm{DB}}=90^{\circ}-30^{\circ}=60^{\circ}$.
Do $\triangle A B \mathrm{D}=\triangle C B \mathrm{D}$ nên $\widehat{A B D}=\widehat{C B D}$ (2 góc tương ứng).
Do đó $\widehat{C B D}=60^{\circ}$.
Khi đó $\widehat{A B C}=\widehat{A B D}+\widehat{C B D}=60^{\circ}+60^{\circ}=120^{\circ}$.
Vậy $\widehat{A B C}=120^{\circ}$.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 13 – Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác trang 63,67 Toán 7 Kết nối tri thức tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





