Giải SGK Bài 31 trang 59, 60, 61, 62 SGK Toán 7 Kết nối tri thức Tập 2
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết tất cả các câu hỏi, vận dụng, luyện tập và bài tập và cùng nhau tìm ra phương pháp giải hay, nhanh nhất cho bài Quan hệ giữa góc và cạnh đối diện trong một tam giác. Các bài tập sau đây thuộc Bài 31 chương 9 trang 59, 60, 61, 62 Toán 7 Kết nối tri thức Tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Giải mục 1 SGK trang 60 Toán 7 Kết nối tri thức tập 2
Với giải bài tập Bài 31 SGK Toán 7 Kết Nối Tri Thức Tập 2: Quan hệ giữa góc và cạnh đối diện trong một tam giác giúp học sinh dễ dàng hiểu và hoàn thiện các bài tập Toán Hình 7 Bài 31.
Giải câu hỏi mở đầu trang 59 SGK Toán 7 Kết nối tri thức tập 2
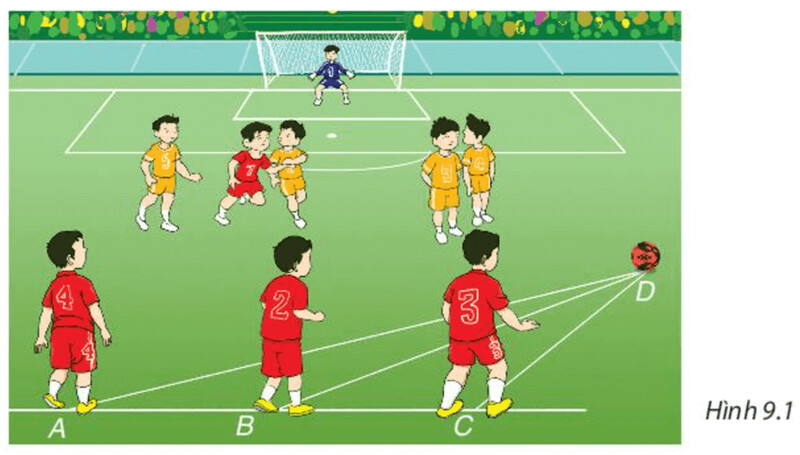
Xét $ \Delta $ $ABD$ có góc $ABD$ là góc tù nên góc $ABD$ là góc lớn nhất trong tam giác.
Khi đó $AD > BD$.
Xét $\Delta$ $BCD$ có góc $BCD$ là góc tù nên góc $BCD$ là góc lớn nhất trong tam giác.
Khi đó $BD > CD$.
Do đó $AD > BD > CD$.
Vậy cầu thủ mang áo số 4 xa trái bóng nhất.
Giải hoạt động 1 trang 60
– Sắp xếp độ dài các cạnh theo thứ tự từ bé đến lớn. Sắp xếp độ lớn các góc theo thứ tự từ bé đến lớn.
– Góc lớn nhất đối diện với cạnh nào? Góc bé nhất đối diện với cạnh nào?
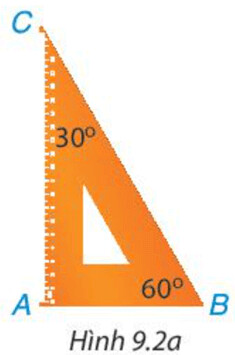
Quan sát, so sánh các cạnh.
– $AB < AC < BC$ nên sắp xếp độ dài các cạnh theo thứ tự từ bé đến lớn là: $AB$, $AC$, $BC$.
$ \widehat{C}$ < $ \widehat{B}$ < $ \widehat{A}$ nên sắp xếp độ lớn các góc theo thứ tự từ bé đến lớn là: $ \widehat{C}$; $ \widehat{B}$; $ \widehat{A}$
– Góc lớn nhất là góc $A$ đối diện với cạnh $BC$. Góc bé nhất là góc $C$ đối diện với cạnh $AB$.
Giải hoạt động 2 SGK trang 60
Quan sát, so sánh các góc.
Giải luyện tập 1 SGK Trang 60
Xác định góc đối diện với từng cạnh rồi so sánh các góc.
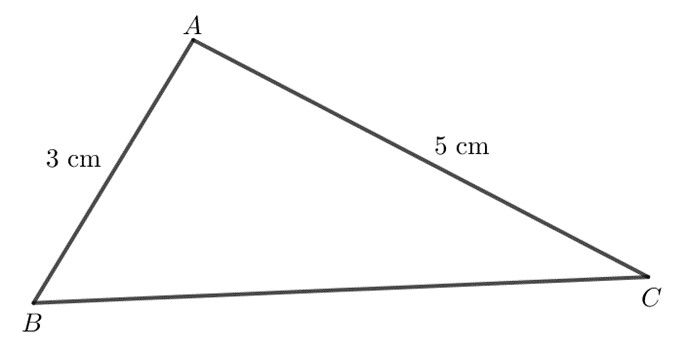
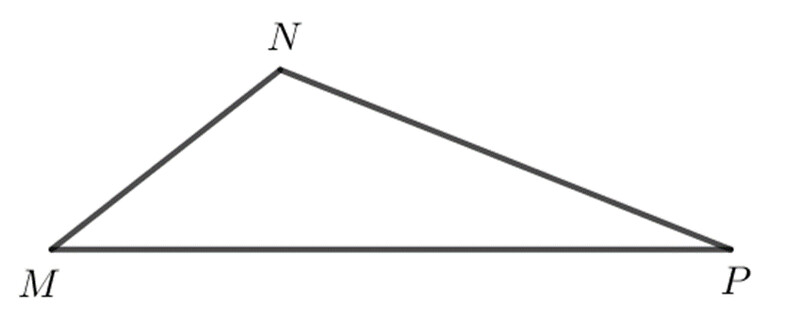
Góc $M$ đối diện với cạnh $NP$
Góc $N$ đối diện với cạnh $MP$.
Ta có: $MN < NP < MP$ nên $\widehat{P}$ < $\widehat{M}$ <$\widehat{N}$ (định lý)
Vậy sắp xếp các góc của tam giác $MNP$ theo thứ tự từ bé đến lớn là: $\widehat{P}$; $\widehat{M}$; $\widehat{N}$
Giải mục 2 Trang 61, 62 SGK Toán 7 Kết nối tri thức tập 2
Cùng HocThatGioi tìm ra đáp án chính xác nhất cho các câu hỏi, luyện tập và vận dụng ở các trang 61, 62 trong bài Quan hệ giữa góc và cạnh đối diện trong một tam giác ở ngay bên dưới nhé!
Giải hoạt động 3 SGK Trang 61
Em hãy dự đoán xem giữa hai cạnh đối diện với hai góc $B$ và $C$ ( tức là cạnh $AC$ và $AB$) thì cạnh nào lớn hơn.
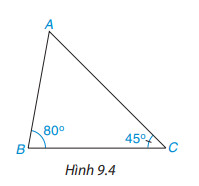
Quan sát, so sánh các cạnh.
Em dự đoán cạnh đối diện với góc $B$ lớn hơn cạnh đối diện với góc $C$.
Giải hoạt động 4 SGK Trang 61
Đo độ dài các cạnh rồi so sánh.
Đo độ dài các cạnh, ta được:
$AB = 3,3 cm$
$AC = 4,6 cm$
Do đó cạnh $AC$ lớn hơn cạnh $AB$
Vậy dự đoán của em ở Hoạt động 3 là đúng.
Giải luyện tập 2 trang 61
+ Áp dụng định lí tổng ba góc trong tam giác, tính góc còn lại của tam giác
+ Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn
Áp dụng định lí tổng ba góc trong một tam giác trong tam giác $MNP$, có:
$\widehat{M}$ + $\widehat{}N$ + $\widehat{P}$ = $180^{\circ}$
$\Longrightarrow $ $47^{\circ}$ + $53^{\circ}$ + $\widehat{P}$ = $180^{\circ}$
$\Longrightarrow $ $\widehat{P}$ = $180^{\circ}$ – $47^{\circ}$ – $53^{\circ}$ = $80^{\circ}$
$\Longrightarrow $ $\widehat{M}$ < $\widehat{}N$ < $\widehat{P}$ ($47^{\circ}$ <$53^{\circ}$ < $80^{\circ}$)
$\Longrightarrow $ $NP < MP < MN$ ( cạnh đối diện với góc lớn hơn thì lớn hơn)
Vậy các cạnh của tam giác đó theo thứ tự độ dài từ bé đến lớn là $NP$, $MP$, $MN$.
Giải phần tranh luận trang 61
Theo em bạn nào nói đúng? Vì sao?

+ Góc tù là góc lớn nhất trong tam giác
+ Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn
Vì tam giác $ABC$ có góc $A$ là góc tù nên góc $A$ là góc lớn nhất trong tam giác $ABC$.
\Longrightarrow Cạnh đối diện với góc $A$ là cạnh lớn nhất trong tam giác $ABC$.
Mà cạnh $BC$ là cạnh đối diện với góc $A$.
Vậy cạnh $BC$ là cạnh lớn nhất trong tam giác $ABC$. Do đó bạn Tròn nói đúng.
Giải bài tập vận dụng trang 62
( Biết rằng góc $ACD$ là góc tù)
Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Trong tam giác $BCD$, góc $DCB$ là góc tù nên là góc lớn nhất. Cạnh $DB$ đối diện với góc lớn nhất nên là cạnh lớn nhất
\Longrightarrow $DB$ > $DC$ (1)
Vì góc $DBA$ là góc ngoài tại đỉnh $B$ của tam giác $BCD$ nên
\widehat{ABD} > \widehat{BCD} nên góc $DBA$ cũng là góc tù.
Trong tam giác $ABD$, góc $DCA$ là góc tù nên là góc lớn nhất. Cạnh $DA$ đối diện với góc lớn nhất nên là cạnh lớn nhất.
\Longrightarrow $DA > DB$ (2)
Từ (1) và (2) \Longrightarrow $DA$ > $DB$ > $DC$
Vậy $DA$ dài nhất, $DC$ ngắn nhất
Do đó, cầu thủ $C$ gần trái bóng nhất, cầu thủ $A$ xa trái bóng nhất.
Giải bài tập trang 62 SGK Toán 7 Kết nối tri thức tập 2
Bài học lý thuyết đã đi đến hồi kết, hãy cùng nhau giải các bài tập trong bài Quan hệ giữa góc và cạnh đối diện trong một tam giác ở các trang 62 SGK Toán 7 Kết nối tri thức tập 2.
Giải bài 9.1 trang 62
a) Tìm cạnh lớn nhất của tam giác $ABC$.
b) Tam giác $ABC$ là tam giác gì?
+ Góc tù là góc lớn nhất trong tam giác. Tam giác có 1 góc tù là tam giác tù.
+ Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn
a) Vì $\widehat{A}$ = $105^{\circ}$ > $90^{\circ}$ nên là góc tù. Do đóc góc $A$ là góc lớn nhất trong tam giác $ABC$.
Cạnh $BC$ đối diện với góc $A$ nên là cạnh lớn nhất trong tam giác $ABC$
Vậy cạnh lớn nhất của tam giác $ABC$ là cạnh $BC$.
b) Vì tam giác có góc $A$ là góc tù
\Longrightarrow Tam giác $ABC$ là tam giác tù.
Giải bài 9.2 trang 62
a) \widehat{A} = \widehat{B}
b) \widehat{A} > \widehat{B}
c) \widehat{A} < \widehat{B}
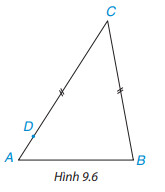
+ So sánh $AC$ và $BC$
+ Sử dụng định lí: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn
Vì $BC = DC$.
Mà $D$ nằm giữa $A$ và $C$ nên $AC$ = $DA$ + $DC$, do đó $AC > DC$
\Longrightarrow $AC$ > $BC$
Xét tam giác $ABC$ có $AC$ > $BC$
\Longrightarrow \widehat{B} > \widehat{A} ( trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn)
Vậy khẳng định c là đúng.
Giải bài 9.3 trang 62
+ Xác định góc bằng $96^{\circ}$ là góc ở đáy hay góc ở đỉnh.
+ Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
+ Góc bằng $96^{\circ}$ không thể là góc ở đáy vì góc ở đáy còn lại cũng bằng $96^{\circ}$. Khi đó, tổng ba góc trong tam giác vượt quá 180 độ ( Vô lí)
Do đó, góc bằng $96^{\circ}$ là góc ở đỉnh. Cạnh đối diện với góc ở đỉnh là cạnh đáy.
+ Vì $96^{\circ}$ là góc tù nên là góc bằng $96^{\circ}$ là góc lớn nhất trong tam giác nên cạnh đáy là cạnh lớn nhất ( trong một tam giác, cạnh đối diện với góc lớn nhất là cạnh lớn nhất)
Giải bài 9.4 trang 62
Biết rằng ba điểm $A$,$B$,$C$ cùng nằm trên một đường thẳng, $B$ nằm giữa $A$ và $C$, \widehat{ACD} là góc tù. Hỏi bạn nào đi xa nhất, bạn nào đi gần nhất? Vì sao?
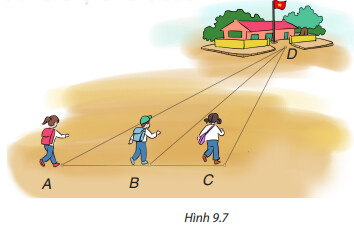
Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Trong tam giác $BCD$, góc $DCB$ là góc tù nên là góc lớn nhất. Cạnh $DB$ đối diện với góc lớn nhất nên là cạnh lớn nhất
\Longrightarrow $DB$ > $DC$ (1)
Vì góc $DBA$ là góc ngoài tại đỉnh $B$ của tam giác $BCD$ nên:
\widehat{ABD} > \widehat{BCD} nên góc $DBA$ cũng là góc tù.
Trong tam giác $ABD$, góc $DCA$ là góc tù nên là góc lớn nhất. Cạnh $DA$ đối diện với góc lớn nhất nên là cạnh lớn nhất.
\Longrightarrow $DA$ > $DB$ (2)
Từ (1) và (2) \Longrightarrow $DA$ > $DB$ > $DC$
Vậy $DA$ dài nhất, $DC$ ngắn nhất. Do đó bạn Mai đi xa nhất, bạn Hà đi gần nhất.
Giải bài 9.5 trang 62
Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn
Xét độ dài $AC$, $BC$ có vượt quá $500 m$ không? Nếu có khoảng cách vượt quá $500 m$ thì tại $C$ không thể nghe tiếng loa.
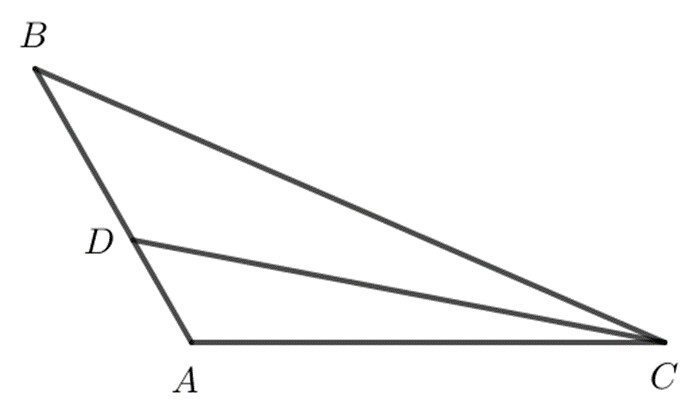
Xét $ \Delta $ $ACD$ có $\widehat{CAD}$ ]à góc tù nên $\widehat{CAD}$ là góc lớn nhất trong $ \Delta $ $ACD$.
Do đó cạnh đối diện với $\widehat{CAD}$ là cạnh lớn nhất trong $ \Delta $ $ACD$.
Cạnh đối diện với $\widehat{CAD}$ trong $ \Delta $ $ACD$ là cạnh $CD$.
Do đó $CD$ > $AC$ = $500 m$.
Bán kính để nghe rõ tiếng của loa là $500 m$ nên tại $C$ không tthể nghe rõ tiếng loa.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Bà viết này đã giải quyết tất cả các bài tập, câu hỏi, các hoạt động của bài Quan hệ giữa góc và cạnh đối diện trong một tam giác. Các bài tập sau đây thuộc Bài 31 chương 9 trang 59, 60, 61, 62 Toán 7 Kết nối tri thức Tập 2. Hy vọng, qua bài viết này bạn có thể nắm rõ tất cả các kiến thức và áp dụng nó vào thực tế một cách tốt nhất. Chúc các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





