SGK Toán 7 – Kết Nối Tri Thức
Giải SGK bài tập cuối chương 8 SGK trang 58 Toán 7 Kết nối tri thức Tập 2
Chương 8 đã dần đi đến hồi kết, phần lý thuyết về chương 8 Làm quen với biến cố và xác suất của biến cố đã tạm khép lại. Sau đây, chúng ta sẽ cùng áp dụng các lý thuyết đã học, để giải các bài tập cuối chương 8 trang 58 SGK Toán 7 Kết nối tri thức tập 2. Cùng xem HocThatGioi giải các bài toán này nhé!
Giải SGK bài 8.12 trang 58
Một túi đựng các quả cầu có cùng kích thước, được ghi số $5; 10; 15; 20; 30; 35; 40$. Lấy ngẫu nhiên một quả cầu trong túi. Chọn từ thích hợp (chắc chắn, không thểm ngẫu nhiên) thay vào dấu “ $?$” trong các câu sau:
– Biến cố $A$: “ Lấy được quả cầu ghi số là số chính phương” là biến cố ..$?$..
– Biến cố $B$: “ Lấy được quả cầu ghi số là số chia hết cho $3$” là biến cố ..$?$..
– Biến cố $C$: “ Lấy được quả cầu ghi số là số chia hết cho $5$” là biến cố ..$?$..
– Biến cố $A$: “ Lấy được quả cầu ghi số là số chính phương” là biến cố ..$?$..
– Biến cố $B$: “ Lấy được quả cầu ghi số là số chia hết cho $3$” là biến cố ..$?$..
– Biến cố $C$: “ Lấy được quả cầu ghi số là số chia hết cho $5$” là biến cố ..$?$..
Phương pháp giải:
Biến cố chắc chắn: Là biến cố biết trước được luôn xảy ra.
Biến cố không thể: Là biến cố biết trước được không bao giờ xảy ra.
Biến cố ngẫu nhiên: Là biến cố không thể biết trước được có xảy ra hay không.
Biến cố chắc chắn: Là biến cố biết trước được luôn xảy ra.
Biến cố không thể: Là biến cố biết trước được không bao giờ xảy ra.
Biến cố ngẫu nhiên: Là biến cố không thể biết trước được có xảy ra hay không.
Lời giải chi tiết:
Biến cố $A$: “Lấy được quả cầu ghi số là số chính phương” là biến cố không thể vì trong số các số được ghi không có số nào là số chính phương.
Biến cố $B$: “Lấy được quả cầu ghi số là số chia hết cho $3$” là biến cố ngẫu nhiên vì trong số các số được ghi, có số 1$5, 30$ chia hết cho $3$.
Biến cố $C$: “Lấy được quả cầu ghi số là số chia hết cho $5$” là biến cố chắc chắn vì tất cả các số được ghi đều chia hết cho $5$.
Biến cố $A$: “Lấy được quả cầu ghi số là số chính phương” là biến cố không thể vì trong số các số được ghi không có số nào là số chính phương.
Biến cố $B$: “Lấy được quả cầu ghi số là số chia hết cho $3$” là biến cố ngẫu nhiên vì trong số các số được ghi, có số 1$5, 30$ chia hết cho $3$.
Biến cố $C$: “Lấy được quả cầu ghi số là số chia hết cho $5$” là biến cố chắc chắn vì tất cả các số được ghi đều chia hết cho $5$.
Giải SGK bài 8.13 trang 58
Một thùng kín đựng $5$ quả bóng màu đỏ, $10$ quả bóng màu xanh, $20$ quả bóng màu vàng, có cùng kích thước. Ngọc lấy ngẫu nhiên một quả bóng trong thùng. Hỏi khả năng Ngọc lấy quả bóng màu gì lớn nhất?
Phương pháp giải:
Số bóng màu nào nhiều hơn thì khả năng lấy được bóng màu đó càng lớn.
Số bóng màu nào nhiều hơn thì khả năng lấy được bóng màu đó càng lớn.
Lời giải chi tiết:
Vì số bóng màu vàng nhiều nhất nên khả năng Ngọc lấy quả bóng màu vàng lớn nhất.
Vì số bóng màu vàng nhiều nhất nên khả năng Ngọc lấy quả bóng màu vàng lớn nhất.
Giải SGK bài 8.14 trang 58
Một chiếc hộp đựng $7$ tấm thẻ như nhau được ghi số $2;3;4;5;6;7;8$. Rút ngẫu nhiên một tấm thẻ trong hộp. Tìm xác suất để rút được tấm thẻ:
a) Ghi số nhỏ hơn $10$.
b) Ghi số $1$.
c) Ghi số $8$.
a) Ghi số nhỏ hơn $10$.
b) Ghi số $1$.
c) Ghi số $8$.
Phương pháp giải:
Biến cố chắc chắn: Là biến cố biết trước được luôn xảy ra. Biến cố chắc chắn có xác suất bằng $1$.
Biến cố không thể: Là biến cố biết trước được không bao giờ xảy ra. Biến cố không thể có xác suất bằng $0$.
Biến cố ngẫu nhiên: Có $k$ biến cố đồng khả năng và luôn xảy ra $1$ trong $k$ biến cố này thì xác suất của mỗi biến cố đó là $\frac{1}{k}$.
Biến cố chắc chắn: Là biến cố biết trước được luôn xảy ra. Biến cố chắc chắn có xác suất bằng $1$.
Biến cố không thể: Là biến cố biết trước được không bao giờ xảy ra. Biến cố không thể có xác suất bằng $0$.
Biến cố ngẫu nhiên: Có $k$ biến cố đồng khả năng và luôn xảy ra $1$ trong $k$ biến cố này thì xác suất của mỗi biến cố đó là $\frac{1}{k}$.
Lời giải chi tiết:
a) Vì biến cố: “Rút được tấm thẻ ghi số nhỏ hơn $10$” là biến cố chắc chắn nên xác suất rút được tấm thẻ ghi số nhỏ hơn $10$ là $1$.
b) Vì biến cố: “Rút được tấm thẻ ghi số $1$” là biến cố không thể nên xác suất rút được tấm thẻ ghi số $1$ là $0$.
c) Biến cố: “Rút được tấm thẻ ghi số $8$” là biến cố ngẫu nhiên.
Có $7$ biến cố đồng khả năng: “Rút được thẻ ghi số $2$” ; “Rút được thẻ ghi số $3$”; “Rút được thẻ ghi số $4$”; “Rút được thẻ ghi số $5$”; “Rút được thẻ ghi số $6$”; “Rút được thẻ ghi số $7$”; “Rút được thẻ ghi số $8$” và luôn xảy ra $1$ trong $7$ biến cố đó.
Xác suất của mỗi biến cố là: $\frac{1}{7}$.
Vậy xác suất rút được thẻ ghi số $8$ là $\frac{1}{7}$.
a) Vì biến cố: “Rút được tấm thẻ ghi số nhỏ hơn $10$” là biến cố chắc chắn nên xác suất rút được tấm thẻ ghi số nhỏ hơn $10$ là $1$.
b) Vì biến cố: “Rút được tấm thẻ ghi số $1$” là biến cố không thể nên xác suất rút được tấm thẻ ghi số $1$ là $0$.
c) Biến cố: “Rút được tấm thẻ ghi số $8$” là biến cố ngẫu nhiên.
Có $7$ biến cố đồng khả năng: “Rút được thẻ ghi số $2$” ; “Rút được thẻ ghi số $3$”; “Rút được thẻ ghi số $4$”; “Rút được thẻ ghi số $5$”; “Rút được thẻ ghi số $6$”; “Rút được thẻ ghi số $7$”; “Rút được thẻ ghi số $8$” và luôn xảy ra $1$ trong $7$ biến cố đó.
Xác suất của mỗi biến cố là: $\frac{1}{7}$.
Vậy xác suất rút được thẻ ghi số $8$ là $\frac{1}{7}$.
Giải SGK bài 8.15 trang 58
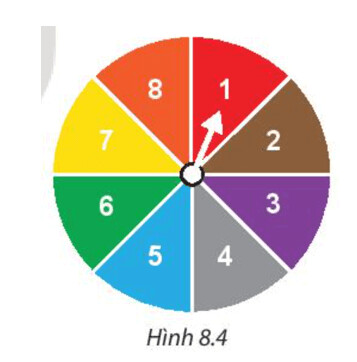
Một tấm bìa cứng hình tròn được chia làm $8$ phần có diện tích bằng nhau và ghi số $1;2;3;4;5;6;7;8$ như $Hình$ $8.4$, được gắn vào trục quay có mũi tên ở tâm.
Bạn Việt quay tấm bìa.
a) Tìm xác suất để mũi tên chỉ vào hình quạt:
* Ghi số lẻ * Ghi số $6$
b) Biết rằng nếu mũi tên dừng ở hình quạt ghi số $1$ hoặc $2$ thì Việt nhận được $100$ điểm; dừng ở hình quạt ghi số $3$ hoặc $4$ thì Việt nhận được $200$ điểm; dừng ở hình quạt ghi số $5$ hoặc $6$ thì Việt nhận được $300$ điểm; dừng ở hình quạt ghi số $7$ hoặc $8$ thì Việt nhận được $400$ điểm.
Xét các biến cố sau:
$A$: “ Việt nhận được $100$ điểm”
$B$: “ Việt nhận được $200$ điểm”
$C$: “ Việt nhận được $300$ điểm”
$D$: “ Việt nhận được $400$ điểm”
Các biến cố $A,B,C,D$ có đồng khả năng hay không?
Tìm xác suất các biến cố $A,B,C$ và $D$.
Bạn Việt quay tấm bìa.
a) Tìm xác suất để mũi tên chỉ vào hình quạt:
* Ghi số lẻ * Ghi số $6$
b) Biết rằng nếu mũi tên dừng ở hình quạt ghi số $1$ hoặc $2$ thì Việt nhận được $100$ điểm; dừng ở hình quạt ghi số $3$ hoặc $4$ thì Việt nhận được $200$ điểm; dừng ở hình quạt ghi số $5$ hoặc $6$ thì Việt nhận được $300$ điểm; dừng ở hình quạt ghi số $7$ hoặc $8$ thì Việt nhận được $400$ điểm.
Xét các biến cố sau:
$A$: “ Việt nhận được $100$ điểm”
$B$: “ Việt nhận được $200$ điểm”
$C$: “ Việt nhận được $300$ điểm”
$D$: “ Việt nhận được $400$ điểm”
Các biến cố $A,B,C,D$ có đồng khả năng hay không?
Tìm xác suất các biến cố $A,B,C$ và $D$.
Phương pháp giải:
Biến cố ngẫu nhiên: Có $k$ biến cố đồng khả năng và luôn xảy ra $1$ trong $k$ biến cố này thì xác suất của mỗi biến cố đó là $\frac{1}{k}$.
Biến cố ngẫu nhiên: Có $k$ biến cố đồng khả năng và luôn xảy ra $1$ trong $k$ biến cố này thì xác suất của mỗi biến cố đó là $\frac{1}{k}$.
Lời giải chi tiết:
a) *Xét $2$ biến cố: “Mũi tên chỉ vào số lẻ” ; “Mũi tên chỉ vào số chẵn”.
Đây là $2$ biến cố đồng khả năng (đều có $4$ khả năng) và luôn xảy ra $1$ trong $2$ biến cố đó
Xác suất của mỗi biến cố đó là $\frac{1}{2}$.
* Xét $8$ biến cố: “Mũi tên chỉ vào số $1$” ; “Mũi tên chỉ vào số $2$”; “Mũi tên chỉ vào số $3$” ; “Mũi tên chỉ vào số $4$”; “Mũi tên chỉ vào số $5$” ; “Mũi tên chỉ vào số $6$”; “Mũi tên chỉ vào số $7$” ; “Mũi tên chỉ vào số $8$”.
Chúng là $8$ biến cố đồng khả năng và luôn xảy ra $1$ trong $8$ biến cố đó.
Xác suất của mỗi biến cố đó là $\frac{1}{8}$.
b) Xét $4$ biến cố: $A,B,C,D$.
$4$ biến cố này là $4$ biến cố đồng khả năng (đều có $2$ khả năng) và luôn xảy ra $1$ trong $4$ biến cố đó
Xác suất của mỗi biến cố đó là $\frac{1}{4}$.
a) *Xét $2$ biến cố: “Mũi tên chỉ vào số lẻ” ; “Mũi tên chỉ vào số chẵn”.
Đây là $2$ biến cố đồng khả năng (đều có $4$ khả năng) và luôn xảy ra $1$ trong $2$ biến cố đó
Xác suất của mỗi biến cố đó là $\frac{1}{2}$.
* Xét $8$ biến cố: “Mũi tên chỉ vào số $1$” ; “Mũi tên chỉ vào số $2$”; “Mũi tên chỉ vào số $3$” ; “Mũi tên chỉ vào số $4$”; “Mũi tên chỉ vào số $5$” ; “Mũi tên chỉ vào số $6$”; “Mũi tên chỉ vào số $7$” ; “Mũi tên chỉ vào số $8$”.
Chúng là $8$ biến cố đồng khả năng và luôn xảy ra $1$ trong $8$ biến cố đó.
Xác suất của mỗi biến cố đó là $\frac{1}{8}$.
b) Xét $4$ biến cố: $A,B,C,D$.
$4$ biến cố này là $4$ biến cố đồng khả năng (đều có $2$ khả năng) và luôn xảy ra $1$ trong $4$ biến cố đó
Xác suất của mỗi biến cố đó là $\frac{1}{4}$.
Hi vọng những bài giải và phương pháp giải trên của HocThatGioi về Bài tập cuối chương 8 trang 58 Toán 7 Kết nối tri thức tập 2 sẽ phần nào giúp các bạn hoàn thành và hiểu trọn vẹn được những bài tập được thầy cô giao cho. Chúc các bạn học tốt!





