Giải SGK bài 20 Động học của chuyển động tròn Vật lí 10 Chân trời sáng tạo
Bài viết sau đây của HocThatGioi sẽ hướng dẫn bạn những phương pháp và lời giải chi tiết nhất, giúp giải quyết toàn bộ các câu hỏi và bài tập trong bài 20 Động học của chuyển động tròn. Các câu hỏi này nằm ở các trang 126, 127, 128, 129, 130 Vật lí 10 Chân trời sáng tạo. Hy vọng các bạn sẽ nắm chắc và hiểu được toàn bộ bài học sau khi xem bài viết dưới đây.
Giải SGK câu hỏi mở đầu trang 126 Vật lí 10 Chân trời sáng tạo
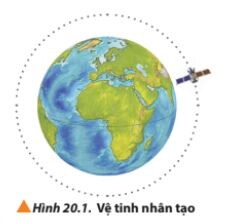
Quan sát hình vẽ.
– Quỹ đạo của vệ tinh nhân tạo của Trái Đất có hình tròn.
– Tốc độ chuyển động của vệ tinh phụ thuộc vào độ cao của vệ tinh đối với Trái Đất (minh chứng sẽ được học trong bài).
Giải SGK mục 1 trang 126, 127 Vật lí 10 Chân trời sáng tạo
Dưới đây là các phương pháp giải và đáp án chính xác nhất cho các câu hỏi hoạt động ở mục 1 Định nghĩa radian. Số đo cung tròn theo góc ở các trang 126, 127 trong bài 20 SGK Vật lí 10 Chân trời sáng tạo. Các bạn có thể tham khảo ở ngay bên dưới nhé!
Giải SGK câu hỏi 1 trang 126

Quan sát hình vẽ và vận dụng kiến thức toán học.
Theo công thức tính chu vi đường tròn có bán kính R, ta có chiều dài của nửa đường tròn bằng πR.
Vì cung tròn của đường tròn có chiều dài là R tương ứng với góc 1 rad nên chiều dài tương ứng với góc π rad.
Giải SGK câu hỏi 2 trang 127
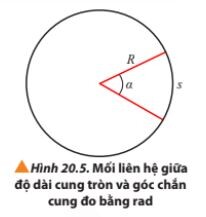
Vận dụng kiến thức đã học.
– Công thức tính chiều dài cung tròn s đã được học là: $s = \frac{\pi \cdot R \cdot \alpha}{180}$
– Trong công thức trên, $\alpha$ được tính theo đơn vị là độ.
– Công thức tính chiều dài đơn giản hơn: $s = \alpha \cdot R$; trong đó $\alpha$ có đơn vị là rad.
Với $\alpha^\circ = \alpha(rad) \cdot \frac{180^\circ}{\pi}$
Giải SGK câu hỏi luyện tập trang 127
$x^\circ = \frac{x \cdot \pi}{180} rad$
| Số đo theo độ | $0^\circ$ | $30^\circ$ | $45^\circ$ | $60^\circ$ | $90^\circ$ | $180^\circ$ | $360^\circ$ |
| Số đo theo radian | $0$ | $\frac {\pi}{6}$ | $\frac {\pi}{4}$ | $\frac {\pi}{3}$ | $\frac {\pi}{2}$ | $\pi$ | $2\pi$ |
Giải SGK câu hỏi 3 trang 127
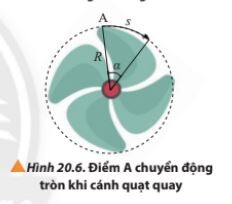
Quãng đường điểm A đi được là: $s = \alpha_{(radian)} \cdot R$
Giải SGK câu hỏi 4 trang 127
Lưu ý khi sử dung biểu thức $s = \alpha \cdot R$ là góc $\alpha$ có đơn vị là radian.
Với $\alpha^\circ = \alpha(rad) \cdot \frac {180^\circ}{\pi}$
Giải SGK mục 2 trang 128, 129 Vật lí 10 Chân trời sáng tạo
Dưới đây là các phương pháp giải và đáp án chính xác nhất cho các câu hỏi hoạt động ở mục 2 Tốc độ trong chuyển động tròn ở các trang 128, 129 trong bài 20 SGK Vật lí 10 Chân trời sáng tạo. Các bạn hãy xem ngay lời giải chi tiết bên dưới dưới nhé!
Giải SGK câu hỏi 5 trang 128
Tốc độ chuyển động của em phụ thuộc vào tốc độ góc (góc quay được trong một đơn vị thời gian).
Giải SGK câu hỏi luyện tập trang 129

Biểu thức tính tốc độ góc: $\omega = \frac {2\pi}{T}$
$T$ là chu kì $(s)$.
Đổi $T = 12 giờ = 12.86400 s = 1.036.800 s$
Tốc độ góc của các vệ tinh là:
$\omega = \frac {2\pi}{T} = \frac {2\pi}{1036800} \approx 6,06\cdot10^{-6} (rad/s)$
Giải SGK câu hỏi 6 trang 129

Biểu thức mối liên hệ giữa vận tốc, tốc độ góc và bán kính: $v = \omega \cdot R$
Tốc độ càng lớn (vật chuyển động càng nhanh) thì mắt càng khó nhìn.
– Trong chuyển động tròn, mỗi điểm trên bán kính đều có cùng tốc độ góc, nhưng vì mỗi điểm này có quãng đường khác nhau nên vận tốc khác nhau.
– Những điểm thuộc phần trục quay có quãng đường nhỏ hơn những điểm ở xa trục trục quay nên vận tốc của những điểm ở gần trục quay nhỏ hơn vận tốc ở những điểm xa trục quay
$\Rightarrow$ Phần cánh quạt ở gần trục quay rõ hơn phần ở xa trục quay.
Giải SGK mục 3 trang 129, 130 Vật lí 10 Chân trời sáng tạo
Dưới đây là những phương pháp và lời giải chi tiết, chính xác nhất cho các câu hỏi luyện tập và vận dụng thuộc mục 3 Gia tốc hướng tâm của chuyển động tròn đều nằm ở các trang 129, 130 bài 20 SGK Vật lí 10 Chân trời sáng tạo. Các bạn có thể tham khảo ngay đáp án bên dưới nhé.
Giải SGK câu hỏi 7 trang 129
Trong chuyển động tròn đều, tuy vận tốc có độ lớn không đổi nhưng lại có phương luôn thay đổi. Vì gia tốc đặc trưng cho sự thay đổi của vận tốc nên chuyển động tròn đều có gia tốc.
Giải SGK câu hỏi vận dụng trang 130
+ Gia tốc hướng tâm của một điểm chính giữa nan hoa xe đạp: $a_{ht} = \omega^2 \cdot R$
+ Ta có $\omega$ luôn không đổi trong quá trình chuyển động, nên những điểm càng xa tâm thì gia tốc càng lớn và ngược lại.
$\Rightarrow$ Gia tốc hướng tâm phụ thuộc vào khoảng cách từ điểm tới tâm.
Giải SGK bài tập trang 130 Vật lí 10 Chân trời sáng tạo
Phần bài tập của bài 20 Động học của chuyển động tròn nằm ở trang 130 SGK Vật lí 10 Chân trời sáng tạo sẽ giúp các bạn củng cố những kiến thức đã được học trong bài. Dưới đây là những phương pháp giải và đáp án chi tiết, chính xác nhất mà các bạn có thể tham khảo. Cùng xem ngay bên dưới nhé!
Giải SGK bài tập 1 trang 130

$\alpha^\circ = \alpha(rad) \cdot \frac {180^\circ}{\pi}$
$\alpha(radian) = \frac {\alpha^\circ \cdot \pi}{180}$
+ $15^\circ = \frac {15 \cdot \pi}{180} = \frac {\pi}{12} radian$
+ $\frac {3\pi}{4} = \frac {3}{4} \cdot 180 = 135^\circ$
+ $150^\circ = \frac {150 \cdot \pi}{180} = \frac {5\pi}{6} radian$
+ $\frac {\pi}{10} = \frac {1}{10} \cdot 180 = 18^\circ$
| Độ | $15^\circ$ | $135^\circ$ | $150^\circ$ | $18^\circ$ |
| Rad | $\frac {\pi}{12}$ | $\frac {3\pi}{4}$ | $\frac {5\pi}{6}$ | $\frac {\pi}{10}$ |
Giải SGK bài tập 2 trang 130
Biểu thức tính chiều dài của một cung tròn: $s = α \ cdot R$
+ $α$ là góc quay (rad)
+ $R$ là bán kính (m)
$\alpha(radian) = \frac {\alpha^\circ \cdot \pi}{180}$
Đổi $200^\circ = \frac {200 \cdot \pi}{180} = \frac {10\pi}{9} (radian)$
$\Rightarrow$ Chiều dài của cung tròn là:
$s = \alpha \cdot R = 200^\circ = \frac {10\pi}{9} \cdot 1,2 \approx 4,2(m)$
Giải SGK bài tập 3 trang 130
+ Biểu thức tính tốc độ: $v = \omega \cdot R$
+ Biểu thức tính gia tốc hướng tâm: $a_{ht} = \omega^2 \cdot R$
Trong đó:
+ $\omega$: tốc độ góc (tốc độ quay trong 1 giây) (rad/s)
+ $R$: khảng cách từ vật đến tâm (m)
Ta có: $\omega= 2 vòng/s = 2.2π = 12,57 rad/s; R = 20 200 + 6400 = 26 600 km = 2,66.10^7 m$
Tốc độ của mỗi vệ tinh là:
$v = \omega \cdot R = 12,57 \cdot 2,66 \cdot 10^7 \approx 3,34 \cdot 10^8 (m/s)$
Gia tốc hướng tâm của mỗi vệ tinh là:
$a_{ht} = \omega^2 \cdot R = 12,57^2 \cdot 2,66 \cdot 10^7 \approx 4,2 \cdot 10^9 (m/s^2)$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Bài viết trên đã giải quyết tất cả các câu hỏi luyện tập, vận dụng cùng các bài tập trong bài 20 Động học của chuyển động tròn ở các trang 126, 127, 128, 129, 130 Vật lí 10 Chân trời sáng tạo. Hy vọng bài viết sẽ giúp các bạn giải đáp được các thắc mắc của mình trong bài học này. Cảm ơn các bạn đã theo dõi, hẹn gặp lại vào các bài viết tiếp theo nhé.





