Dạng bài tập tìm quãng đường trong dao động điều hoà – cách giải và bài tập
Trong bài này, HocThatGioi sẽ chia sẻ cho các bạn về Dạng bài tập tìm quãng đường trong dao động điều hoà – cách giải và bài tập, bài viết sẽ giúp chúng ta bài viết sẽ giúp ta biết được cách tính quãng đường trong dao động điều hoà, cũng sẽ có những bài tập rèn luyện để giúp chúng ta thực hành và làm ngon lành dạng bài tập này nhé!
Trong dạng bài tập này thường có 2 loại tìm quãng đường:
- Tìm quãng đường vật đi được trong một khoảng thời gian
- Tìm quảng đường ngắn nhất, quãng đường dài nhất trong một khoảng thời gian
1. Cách giải dạng bài tập tính quãng đường vật đi được trong một khoảng thời gian
Sau đây sẽ là cách giải dạng bài tập tính quãng đường vật đi trong một khoảng thời gian
1.1 Các bước giải bài tập tính quãng đường
Bước 1: Tìm khoảng thời gian \delta t mà vật đi.
Nếu giả thuyết không cho khoảng thời gian thì ta phải tìm khoảng thời gian bằng hiệu của thời gian cuối và thời gian vật bắt đầu chuyển động:
t_2 là thời gian vật bắt đầu chuyển động
t_1 là thời gian kết thúc
Bước 2: Tách \Delta t=n.T+t' với n=\frac{1}{4},\frac{1}{2},1,2,3,....
Với khoảng thời gian bằng n.T thì:
- Nếu n=\frac{1}{4} thì quãng đường vật đi được là A
- Nếu n=\frac{1}{2} thì quãng đường vật đi được là 2A
- Nếu n là các số nguyên lớn hơn 1 thì quãng đường vật đi được là n.4.A
Với khoảng thời gian bằng t' thì ta cần tính ra góc quét của vật trong khoảng thời gian đó, sau đó dùng vòng tròn dao động điều hoà để xác định vị trí điểm đầu, điểm cuối rồi tính được quãng đường vật đi được trong khoảng thời gian t'
Vậy quãng đường đi được sẽ bằng tổng của quãng đường đi trong khoảng thời gian n.T và quãng đường đi trong khoảng thời gian t'
1.2 Ví dụ minh hoạ
Dưới đây là ví dụ hướng dẫn giải dạng bài tập tính quãng đường đi được trong 1 khoảng thời gian
Chu kì của dao động là: T=\frac{2\pi}{\omega}=\frac{2\pi}{4\pi}=0.5s
Tách \Delta t=2.125=4.0,5+0,125=4.T+0.125
Ta có:
Trong 4T thì vật đi được quãng đường là S_1=4.4.A=16A=128cm
Trong khoảng thời gian 0,125s thì góc quét của vật: \Delta \varphi=\omega.\Delta t=4\pi.0,125=\frac{\pi}{2}
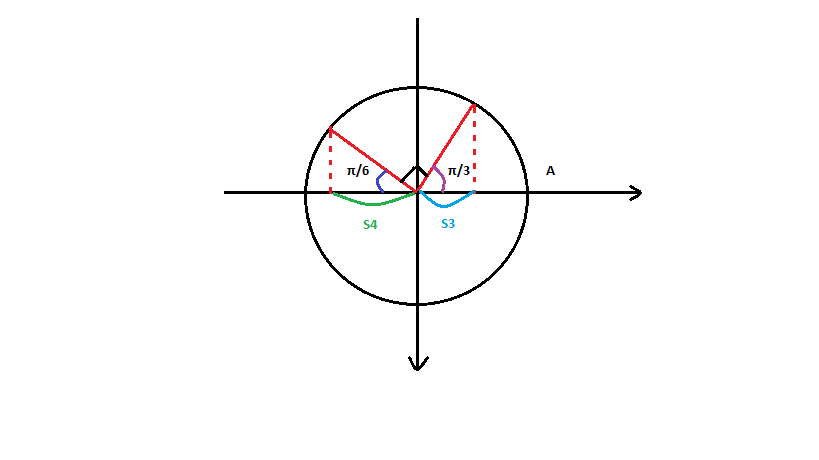
Vẽ vòng tròn dao động điều hoà và dựa vào hình vẽ ta tính được quãng đường vật đi trong khoảng thời gian 0,125s là S_2=S_3+S_4=A.cos(\frac{\pi}{3})+A.cos(\frac{\pi}{6})=4+4\sqrt{3}\approx10,9cm
Vậy quãng đường vật đi được trong khoảng thời gian 2,125s là S=S_1+S_2=128+10,9=138,9cm
1.3 Bài tập rèn luyện
Các bài tập dưới đây sẽ giúp các bạn rèn luyện tốt dạng bài tập này:
2. Cách giải dạng bài tập tìm quãng đường dài nhất, quãng đường ngắn nhất đi trong khoảng thời gian nhỏ hơn nữa chu kì
Các công thức dưới đây chỉ áp dụng đối với khoảng thời gian nhỏ hơn \frac{T}{2}
2.1 Công thức tính quãng đường ngắn nhất và quảng đường dài nhất đi được trong một khoảng thời gian
Công thức tính quãng đường ngắn nhất(S_{min}):
\Delta \varphi=\omega .t
Công thức tính quãng đường dài nhất(S_{max}):
\Delta \varphi=\omega .t
2.2 Ví dụ minh hoạ
Dưới đây là ví dụ hướng dẫn giải dạng bài tập tính quãng đường ngắn nhất, quãng đường dài nhất:
Ta có: 0,2<\frac{T}{2}
Nên ta áp dụng công thức:
S_{max}=2Asin(\frac{\Delta varphi}{2})=2.5.sin(\frac{2\pi.0,2}{2})\approx 5,88cm
2.3 Bài tập rèn luyện
Các bài tập dưới đây sẽ giúp các bạn rèn luyện tốt dạng bài tập này:
Cảm ơn các bạn đã xem hết bài viết của HocThatGioi về Dạng bài tập tìm quãng đường trong dao động điều hoà – cách giải và bài tập, hi vọng sẽ giúp các bạn học tốt về dạng bài tập này. Nếu thấy hay hãy chia sẻ cho bạn bè cùng học và đừng quên để lại 1 like, 1 cmt để tạo động lực và giúp HocThatGioi ngày càng phát triển nhé!
Bài viết khác liên quan đến Lớp 12 – Vật Lý – Dao động điều hòa
- Lý thuyết dao động điều hoà đầy đủ chi tiết nhất – 9 dạng bài hay gặp
- Cách viết phương trình dao động điều hoà – bài tập áp dụng
- Tổng hợp dao động điều hoà – cách viết phương trình dao động tổng hợp và bài tập áp dụng
- 16 bài tập trắc nghiệm dao động điều hoà có đáp án chi tiết nhất
- Dạng bài tập tìm li độ của vật tại một thời điểm – cách giải chi tiết dễ hiểu nhất
- 5 bài tập về dao động điều hoà có lời giải chi tiết