Giải SGK bài 20 Một số ví dụ về cách giải các bài toán thuộc phần động lực học Vật lí 10 Kết nối tri thức
Trong bài viết này HocThatGioi sẽ cùng bạn đi tìm đáp án và phương pháp tốt nhất giải quyết toàn bộ các câu hỏi và bài tập trong bài Một số ví dụ về cách giải các bài toán thuộc phần động lực học. Các bài tập sau đây thuộc bài 20 chương 3 ở các trang 80, 81, 82 Vật lí 10 Kết nối tri thức. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Giải SGK mục 1, 2, 3 SGK trang 80, 81, 82 Vật lí 10 Kết nối tri thức
Cùng HocThatGioi tìm ra đáp án chính xác nhất cho các câu hỏi hoạt động ở Mục 1, 2, 3 của các trang 80, 81, 82 trong bài Một số ví dụ về cách giải các bài toán thuộc phần động lực học ở ngay bên dưới nhé!
Giải SGK câu hỏi 1 trang 82
Các bước giải bài toán phần động lực học:
+ Bước $1$: Phân tích lực tác dụng lên vật
+ Bước $2$: Chọn hệ quy chiếu
+ Bước $3$: Viết phương trình theo định luật $2$ $Newton$: $\sum \overrightarrow{F} = m.\overrightarrow{a}$
+ Bước $4$: Chiếu phương trình định luật $2$ $Newton$ lên trục $Ox$ và $Oy$ $\Rightarrow $ Đại lượng cần tính
Vật chịu tác dụng của $4$ lực: lực đẩy $\overrightarrow{F}$, lực ma sát $\overrightarrow{F_{m}}$, trọng lực $\overrightarrow{P}$, phản lực $\overrightarrow{N}$
Chọn hệ quy chiếu và các lực có chiều như hình vẽ
Theo định luật $2$ $Newton$, ta có: $\overrightarrow{F} + \overrightarrow{F_{m}} + \overrightarrow{P}+ \overrightarrow{N}$ ($1$)
Chiếu ($1$) lên trục $Ox$ ta có: $F – F_{m}= m.a \Leftrightarrow F – \mu N = ma$ ($2$)
Chiếu ($1$) lên $Oy$, ta có:
$P−N=0\Leftrightarrow N=P=mg$
Thay $N = mg$ vào ($2$), ta có:
$F−\mu mg=ma$
$\Leftrightarrow a=\frac{F – \mu mg}{m}$
$\Leftrightarrow a=\frac{220 – 0,35 . 55. 9,8}{55} = 0,57(m/s^{2})$
Giải SGK câu hỏi 2 trang 82
Các bước giải bài toán phần động lực học:
+ Bước $1$: Phân tích lực tác dụng lên vật
+ Bước $2$: Chọn hệ quy chiếu
+ Bước $3$: Viết phương trình theo định luật $2$ $Newton$: $\sum \overrightarrow{F} = m.\overrightarrow{a}$
+ Bước $4$: Chiếu phương trình định luật $2$ $Newton$ lên trục $Ox$ và $Oy \Rightarrow $ Đại lượng cần tính
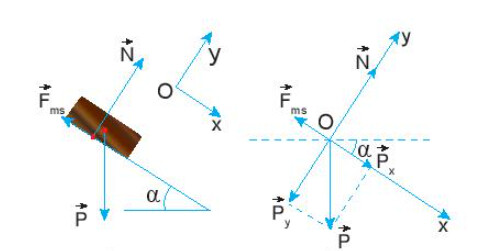
Theo định luật $2$ $Newton$, ta có:
$\overrightarrow{F_{ms}}+ \overrightarrow{P} + \overrightarrow{N}= m.\overrightarrow{a} $ ($1$)
Chiếu ($1$) lên $Ox$, ta có:
$P_{x}−F_{ms}=ma$
$\Leftrightarrow mgsin\alpha − \mu N=ma$ ($2$)
Chiếu ($1$) lên $Oy$, ta có:
$N−P_{y}=0$
$\Leftrightarrow N−mgcos\alpha =0$
$\Leftrightarrow N=mgcos\alpha $
Thay $N=mgcos\alpha$ vào ($2$), ta có:
$mgsin\alpha − \mu mgcos\alpha =ma$
$\Leftrightarrow gsin\alpha −\mu gcos\alpha =a$
$\Leftrightarrow a=9,8.sin30^{\circ}−0,3.9,8.cos30^{\circ}$
$\Leftrightarrow a\approx 2,35(m/s^{2})$
Quãng đường vật đi được sau $2 s$ là:
$S=\frac{1}{2}at^{2}=12.2,35.22=4,7$ $(m)$
Giải SGK bài 3 trang 82
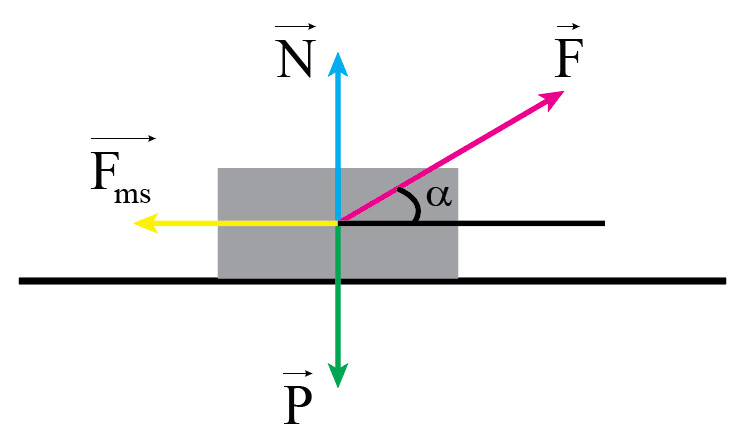
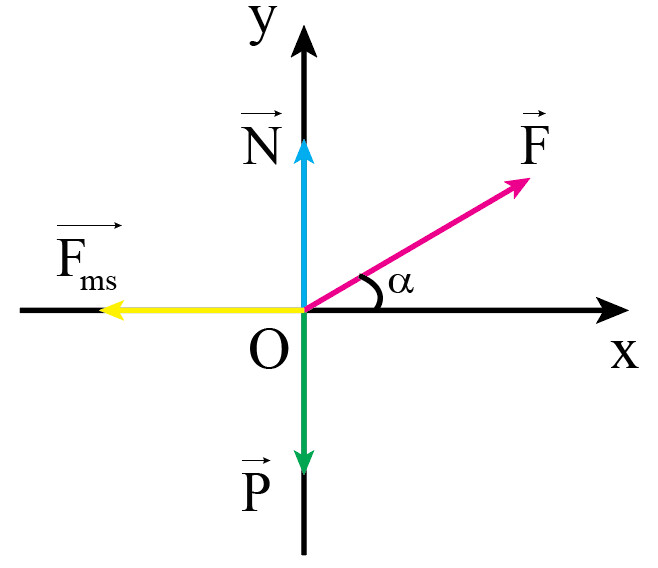
– Vật chuyển động thẳng đều.
– Áp dụng định luật $2$ $Newton$ cho chuyển động của vật theo hai trục $Ox, Oy$:
$\begin{cases} O_{x} : F_{x} = F. cos\alpha – F_{ms} = m.a_{x} = 0 (1)) \\ \\ O_{y} : F_{y} = N + F sin\alpha – P = 0 \end{cases}$ ($2$)
Mà $F_{ms} = \mu .N$
Giải hệ phương trình có:
Từ ($2$) $\Rightarrow N = P – F.sin\alpha = mg – F.sin\alpha$
$\Rightarrow F_{ms} = \mu .N = \mu mg – \mu F.sin\alpha $
Thay vào ($1$) ta được:
$F.cos\alpha – \mu mg + \mu F.sin\alpha = 0 \Rightarrow F = \frac{\mu mg}{cos\alpha +\mu .sin\alpha} = 20,3N$
Giải SGK câu hỏi 4 trang 82
Vật $1$: lực kéo, trọng lực, phản lực, lực ma sát, lực căng dây.
Vật $2$: lực căng dây, phản lực, lực ma sát, trọng lực.
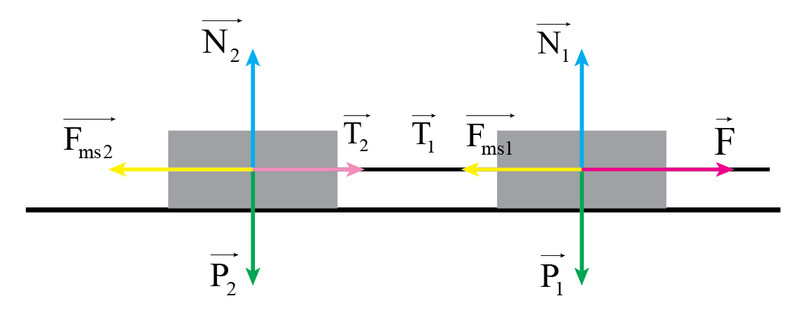
Vật $1$:
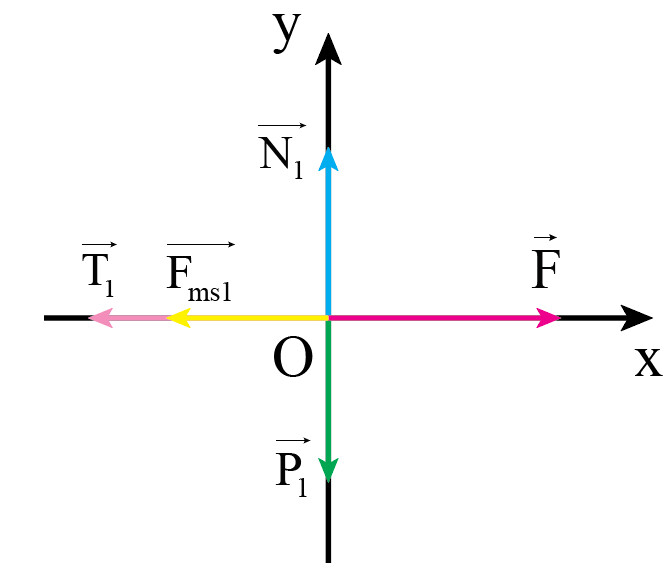
– Áp dụng định luật $2$ $Newton$ cho chuyển động của vật $1$ theo hai trục $Ox, Oy$:
$\begin{cases} O_{x}:F_{x}=F−F_{ms1}−T_{1}=m_{1}.a_{x}=m_{1}a_{1} (1) \\ O_{y}:F_{y}=N_{1}−P_{1}=0 (2) \end{cases}$
Mà $F_{ms1} = \mu .N_{1}$
Giải hệ phương trình có:
Từ $(2)$ ta được: $N_{1} = P_{1} = m_{1}g$
\Rightarrow $F_{ms1} = \mu .N_{1} = \mu m_{1}g$
Thay vào $(1)$ ta được:
$\Rightarrow F – \mu m_{1}g – T_{1} = m_{1}a_{1} \Rightarrow T_{1} = F – \mu m_{1}g – m_{1}a_{1}$
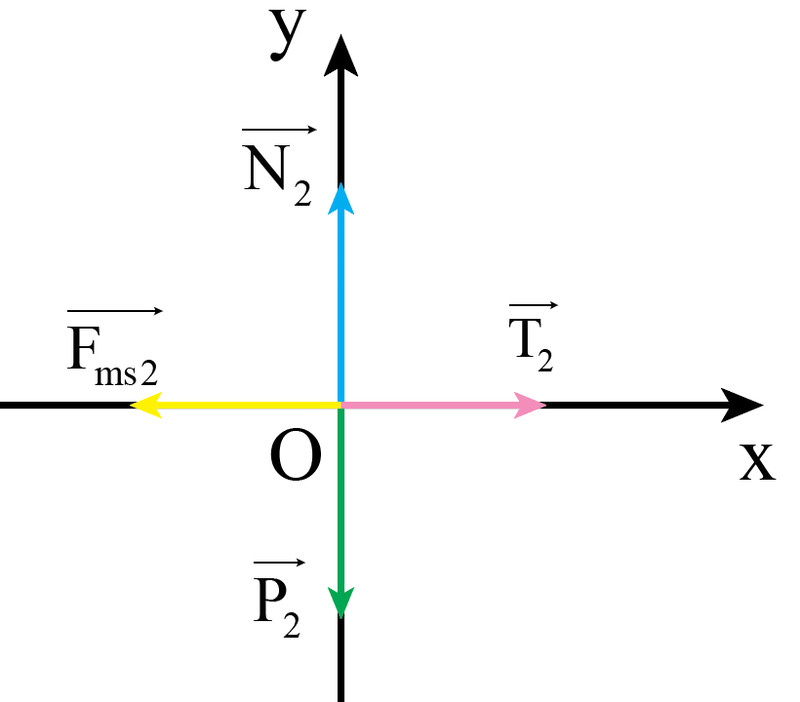
– Áp dụng định luật $2$ $Newton$ cho chuyển động của vật $1$ theo hai trục $Ox, Oy$:
$\begin{cases} O_{x}:F_{x}=T_{2}−F_{ms2}=m_{2}.a_{x}=m_{2}a_{2}(3) \\ O_{y}:F_{y}=N_{2}−P_{2}=0(4)\end{cases}$
Mà $F_{ms2} = \mu .N_{2}$
Giải hệ phương trình có:
Từ $(4)$ ta được: $N_{2} = P_{2} = m_{2}g$
\Rightarrow $F_{ms2} = \mu .N_{2} = \mu m_{2}g$
Thay vào $(3)$ ta được:
$\Rightarrow T_{2} – \mu m_{2}g = m_{2}a_{2} \Rightarrow T_{2} = \mu m_{2}g – m_{2}a_{2}$
Do hệ $2$ vật được nối với nhau bằng một sợi dây không dãn nên ta có:
$T_{1} = T_{2} \Rightarrow F – \mu m_{1}g – m_{1}a_{1} = \mu m_{2}g + m_{2}a_{2}$
Bên cạnh đó hệ hai vật chuyển động với cùng gia tốc nên ta có: $a_{1} = a_{2} = a$
$\Rightarrow F – \mu m_{1}g – m_{1}a = \mu m_{2}g + m_{2}a$ $\Rightarrow a = \frac{F−\mu m_{1}g−\mu m_{2}g}{m_{1}+m_{2}} = 1,04m/s^{2}$
Lực căng dây nối: $T_{1} = T_{2} = \mu m_{2}g + m_{2}a = 30N$
Cách khác: có thể viết định luật $2$ $Newton$ cho hệ $2$ vật vào một phương trình đều được, khi đó biện luận cho lực căng dây, gia tốc để giải ngắn gọn hơn.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Bài viết này đã giải quyết tất cả các bài tập, câu hỏi của bài 20 Một số ví dụ về cách giải các bài toán thuộc phần động lực học chương 3 trang 80, 81, 82 Vật lí 10 Kết nối tri thức. Chúc các bạn học tốt và tiếp thu được nhiều kiến thức bổ ích nhé!





