Giải SGK bài 22 Ba đường Conic trang 48, 49, 50, 51, 52, 53, 54, 55, 56, 57 Toán 10 Kết nối tri thức Tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Ba đường Conic. Đây là bài học thuộc bài 22 chương VII trang 48, 49, 50, 51, 52, 53, 54, 55, 56, 57 sách Toán 10 Kết nối tri thức tập 2. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi trong SGK của bài 22
Dưới đây là phương pháp và bài giải chi tiết cho câu hỏi hoạt động cùng phần luyện tập ở các trang 48, 49, 50, 51, 52, 53, 54, 55, 56 trong bài Ba đường Conic. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động 1 trang 48
a) Đường vừa nhận được có liên hệ với hình ảnh nào ở Hình 7.17?
b) Trong quá trình đầu bút di chuyển để vẽ nên đường nói trên, tổng các khoảng cách từ nó tới các vị trí $F_1 ; F_2$, có thay đổi không? Vì sao?
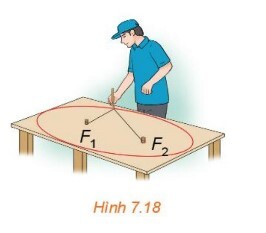
a) Đường vừa nhận được là đường “màu đỏ” trong Hình $7.17$.
b) Tổng khoảng cách từ đầu bút đến các vị trí không thay đổi
Câu hỏi trang 49
Cần điều kiện $a \gt c$ hay $2 a \gt 2 c$ tức là $M F_1+M F_2 \gt F_1 F_2$, nói cách khác là để điểm $\mathrm{M}$ nằm ngoài đoạn $F_1 F_2$, từ đó mới tạo thành elip.
Không tồn tại $\mathrm{M}$ để $M F_1+M F_2 \lt F_1 F_2$ (hay a $ \lt $ c)
Nếu $M F_1+M F_2=F_1 F_2$ thì M thuộc đoạn $F_1 F_2$ cũng không tạo thành elip.
Luyện tập 1 trang 49
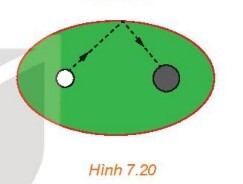
Quãng đường từ lúc bi lăn đến lúc về lỗ thu bi bằng tổng khoảng cách từ điểm bi chạm vào thành bàn tới hai tiêu điểm, dựa vào định nghĩa elip, tổng này luôn bằng $2 a$ không đổi.
Hoạt động 2 trang 49
a) Nêu toạ độ của các tiêu điểm $F_{1}, F_{2}$
b) Giải thích vì sao điểm $M(x ; y)$ thuộc elip khi và chỉ khi:
$$\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2 a \text {. }$$ (1)
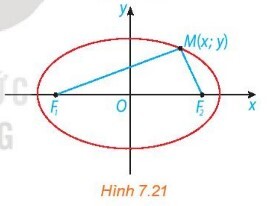
a) Tọa độ 2 tiêu điểm là: $F_1(-c ; 0), F_2(c ; 0)$.
b) Ta có: $M F_1=\sqrt{(x+c)^2+y^2}, M F_2=\sqrt{(x-c)^2+y^2}$.
Vậy để điểm $\mathrm{M}$ thuộc Elip thì khoảng cách $M F_1+M F_2=2 a$ nên $\sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2}=2 a$
Luyện tập 2 trang 50
$\operatorname{Tìm} c=\sqrt{a^2-b^2}$, sau đó thay vào công thức xác địinh hai tiêu điểm và tiêu cự
Ta có: $c=\sqrt{100^2-64^2}=6$.
Do đó $(\mathrm{E})$ có hai tiêu điểm là $F_1(-6 ; 0), F_2(6 ; 0)$ và có tiêu cự bằng $2 c=12$.
Vận dụng 1 trang 50
$$\frac{x^{2}}{16}+\frac{y^{2}}{4}=1 \text {. }$$
Biết rằng 1 đơn vị trên mặt phẳng toạ độ của bản vẽ thiết kế ứng với $30 \mathrm{~cm}$ trên thực tế. Tính chiều cao $h$ của ô thoáng tại điểm cách điểm chính giữa của đế ô thoáng $75 \mathrm{~cm}$.
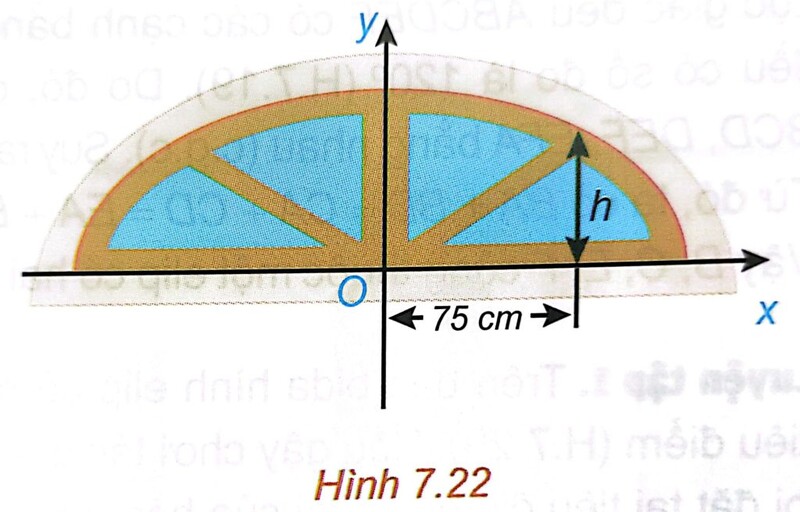
$75 \mathrm{~cm}$ trên bản vẽ ứng với 2,5 đơn vị trên mặt phẳng tọa độ.
Gọi M là điểm trên vòm ô thoáng, có hoành độ 2,5 và tung độ là h.
M thuộc elip nên $\frac{2,5^2}{16}+\frac{h^2}{4}=1$
$$\Leftrightarrow h=\sqrt{4 .\left(1-\frac{2,5^2}{16}\right)}=\frac{\sqrt{39}}{4} \approx 1,56$$
Vậy độ cao h trên thực tế là: $h=1,56.30=46,8 \mathrm{~cm}$
Câu hỏi trang 50
Giả sử $M F_1 \gt M F_2$, ta có:
$$\left|M F_1-M F_2\right|=M F_1-M F_2=M F_1+F_1F_2-\left(M F_2+F_2 F_1\right)$$
Mà M F_2+F_2 F_1 \gt M F_1 \\\\ \Rightarrow\left|M F_1-M F_2\right| \lt M F_1+F_1 F_2-M F_1=F_1 F_2
Hay $2 a \lt 2 c \Leftrightarrow a \lt c$
Luyện tập 3 trang 51
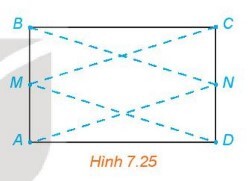
$$|A M-A N|=|B M-B N|=|C M-C N|=|D M-D N| \lt M N \text {. }$$
Ta có: $A M=B M=C N=D N, A N=B N=C M=D M$.
Từ đó suy ra:
$$|A M-A N|=|B M-B N|=|C M-C N|=|D M-D N| \text {. }$$
Và $|AM-AN| \lt M N$ (bất đẳng thức trong tam giác)
Vậy bốn điểm $A, B, C, D$ cùng thuộc một đường hyperbol với $\mathrm{M}, \mathrm{N}$ là hai tiêu điểm.
Hoạt động 3 trang 51
\begin{vmatrix} \sqrt{ (x+c)^2 + y^2 }-\sqrt{ (x-c)^2 + y^2 } \end{vmatrix} \\\\ =2a (3)
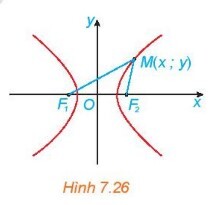
Ta có: $M F_1=\sqrt{(x+c)^2+y^2}, M F_2=\sqrt{(x-c)^2+y^2}$.
Vậy để điểm $M$ thuộc Hyperbol khi và chỉ khi \begin{vmatrix} \sqrt{ (x+c)^2 + y^2 }-\sqrt{ (x-c)^2 + y^2 } \end{vmatrix} \\\\ =2a
Luyện tập 4 trang 52
Tìm $c=\sqrt{a^2+b^2}$, sau đó thay vào công thức xác định hai tiêu điểm và tiêu cự.
Ta có: $c=\sqrt{144+25}=13$.
Do đó $(\mathrm{H})$ có hai tiêu điểm là $F_1(-13 ; 0), F_2(13 ; 0)$ và có tiêu cự bằng $2 c=26$.
Hoạt động 4 trang 52
Xét $\mathrm{F}(0 ; 1)$ và đường thẳng $\Delta: y+1=0$. Với điểm $\mathrm{M}(\mathrm{x}$;y) bất kì, chứng minh rằng $M F=d(M, \Delta) \Leftrightarrow M(x y)$ thuộc (P).
Ta có: $M F=\sqrt{x^2+(y-1)^2}, d(M, \Delta)=|y+1|$.
Xét M F=d(M, \Delta) \\\\ \Leftrightarrow \sqrt{x^2+(y-1)^2}=|y+1| \\\\ \Leftrightarrow x^2+(y-1)^2=(y+1)^2 \\\\ \Leftrightarrow x^2=4 y \\\\ \Leftrightarrow y=\frac{1}{4} x^2.
Vậy tập hợp điểm $\mathrm{M}$ để $M F=d(M, \Delta)$ là parabol $y=\frac{1}{4} x^2$
Hoạt động 5 trang 52
a) Nêu toạ độ của $F$ và phương trình của $\Delta$.
b) Giải thích vì sao điểm $M(x ; y)$ thuộc $(P)$ khi và chỉ khi:
$$\sqrt{\left(x-\frac{p}{2}\right)^{2}+y^{2}}=\left|x+\frac{p}{2}\right| \text {. }$$
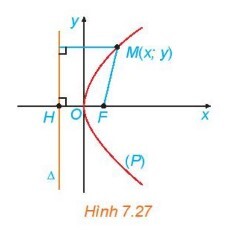
a) Tọa độ điểm $\mathrm{F}$ là: $F\left(\frac{p}{2} ; 0\right)$ và phương trình đường chuẩn là: $\Delta: x=-\frac{p}{2}$
b) Ta có: $M F=\sqrt{\left(x-\frac{p}{2}\right)^2+y^2}, d(M, \Delta)=\left|x+\frac{p}{2}\right|$.
Để $M$ thuộc $(\mathrm{P})$ thì $M F=d(M, \Delta) \Leftrightarrow \sqrt{\left(x-\frac{p}{2}\right)^2+y^2}=\left|x+\frac{p}{2}\right|$
Vận dụng 2 trang 53
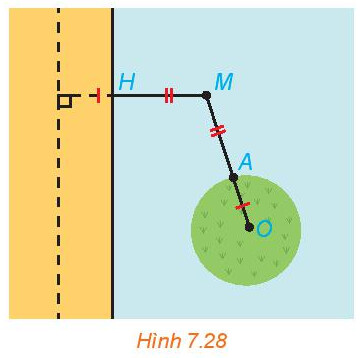
Lấy d là đường thẳng song song với bờ biển và cách bờ biển một khoảng bằng bán kính $\mathrm{OA}$.
Gọi d là đường thẳng nằm trong đất liền, song song với bờ biển và cách bờ biển một khoảng bằng bán kính $O A$.
Ta có: $d(M, d)=M H+R=M A+A O=M O$
Vậy tập hợp điểm $\mathrm{M}$ thuộc $(\mathrm{P})$ có tiêu điểm là $\mathrm{O}$. Đường chuẩn là $\mathrm{d}$.
Do đó đường ranh giới cần tìm là đường parabol (P).
Vận dụng 3 trang 56
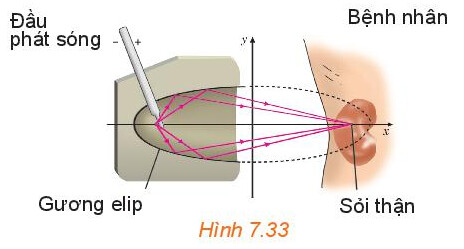
Vị tri bắt đầu phát sóng của máy và vị trí viên sỏi được đặt ở hai tiêu điểm của gương elip, do đó khoảng cách cần tìm là tiêu cự của gương và bằng $2 c=2 \sqrt{400-76}=36(\mathrm{~cm})$.
Giải bài tập vận dụng trang 56 SGK Toán 10 bài 22
Phần tiếp theo sẽ cung cấp cho các bạn phương pháp cùng lời giải trong phần bài tập trang 56 cực kỳ dễ hiểu và chi tiết. Cùng HocThatGioi rèn luyện và nâng cao kỹ năng giải quyết các vấn đề thực tế thông qua các phương pháp, công thức toán học từ bài Ba đường Conic ở trên.
Bài tập 7.19 trang 56
Tính $c=\sqrt{a^2-b^2}$,
+ Tiêu điểm: $F_1(-c ; 0), F_2(c ; 0)$
+ Tiêu cự: $F_1 F_2=2 c$.
Ta có: $a^2=36, b^2=9 \Rightarrow c=\sqrt{36-9}=3 \sqrt{3}$ nên elip có hai tiêu điểm là:
$F_1(-3 \sqrt{3} ; 0) ; F_2(3 \sqrt{3} ; 0)$ và tiêu cự là $F_1 F_2=2 c=6 \sqrt{3}$.
Bài tập 7.20 trang 56
Tính $c=\sqrt{a^2+b^2}$,
+ Tiêu điểm $F_1(-c ; 0), F_2(c ; 0)$
+ Tiêu cự $F_1 F_2=2 c$.
Ta có: $a^2=7, b^2=9 \Rightarrow c=\sqrt{7+9}=4$ nên elip có hai tiêu điểm là:
$F_1(-4 ; 0) ; F_2(4 ; 0)$ và tiêu cự là $F_1 F_2=2 c=8$.
Bài tập 7.21 trang 56
Tìm p, sau đó dựa vào công thức xác định tiêu điểm $F\left(\frac{p}{2} ; 0\right)$ và đường chuẩn là $x=\frac{-p}{2}$ để kết luận.
Ta có: $2 p=8 \Rightarrow p=4$ nên $(\mathrm{P})$ có tiêu điểm là $F(2 ; 0)$ và đường chuẩn là $x=-2$.
Bài tập 7.22 trang 56
Gọi phương trình chính tắc của ( $\mathrm{E}$ ), sau đó thay tọa điểm $\mathrm{A}$ vào phương trình (E) và sử dụng $a^2-b^2=c^2$ để tìm $a, b$.
Phương trình chính tắc của elip có dạng: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$.
Elip đi qua $A(5 ; 0)$ nên ta có $\frac{5^2}{a^2}+\frac{0^2}{b^2}=1 \Leftrightarrow a^2=25$
Mặt khác elip có một tiêu điểm $F_2=(3 ; 0)$ nên ta có $c=3$.
Suy ra $b^2=a^2-c^2=25-3^2=16$
Vậy phương trình của elip là: $\frac{x^2}{25}+\frac{y^2}{16}=1$.
Bài tập 7.23 trang 56
Gọi phương trình chính tắc của (P), sau đó thay tọa điểm $\mathrm{M}$ vào phương trình (P) để tìm được tham số tiêu p.
Phương trình chính tắc của ( $\mathrm{P})$ có dạng $y^2=2 p x(p>0)$
$\mathrm{V}_{\mathrm{i}}(\mathrm{P})$ đi qua điểm $M(2 ; 4)$ nên ta có $4^2=2 p .2 \Leftrightarrow p=4$.
Vậy phương trình chính tắc của $(\mathrm{P})$ là $y^2=8 x$.
Bài tập 7.24 trang 56
Gắn hệ trục tọa độ, sau đó tìm phương trình hyperbol đi qua vị trí tàu thủy
Gọi $\mathrm{M}$ là vị trí tàu thu tín hiệu.
Gọi $t_A, t_B$ lần lượt là thời gian tín hiệu truyền từ trạm phát $\mathrm{A}, \mathrm{B}$ đến $\mathrm{M}$.
Theo đề bài, ta có: $t_A-t_B=-0,0005 s$
Suy ra: $M A-M B=v . t_A-v \cdot t_B=292000 .(-0,0005)=-146 \mathrm{~km}$.
Gọi (H) là hyperbol ở dạng chính tắc nhận $A, B$ làm hai tiêu điểm và đi qua $M$.
Khi đó ta có:
\begin{cases} 2 a = | M A – M B | = 1 4 6 \\ 2 c = A B = 3 0 0 \\ \end{cases} \Rightarrow \begin{cases} a = 7 3 \\ c = 1 5 0\\ \end{cases} \Rightarrow \begin{cases} a=73 \\ b^2=c^2-a^2=17171 \\ \end{cases}
Vậy phương trình chính tắc của $(\mathrm{H})$ là: $\frac{x^2}{5329}-\frac{y^2}{17171}=1$.
Bài tập 7.25 trang 56
a) Lập phương trình chính tắc của $(P)$, với 1 đơn vị đo trong mặt phẳng toạ độ tương ứng $1 \mathrm{~m}$ trên thực tế.
b) Lập phương trình chính tắc của $(P)$, với 1 đơn vị đo trong mặt phẳng toạ độ tương ứng $1 \mathrm{~km}$ trên thực tế.
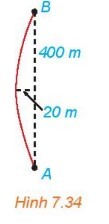
Gọi phương trình chính tắc của $(\mathrm{P})$ và sử dụng điều kiện $(\mathrm{P})$ đi qua điểm thỏa mãn để tìm phương trình $(\mathrm{P})$.
Phương trình chính tắc của parabol (P) có dạng $y^2=2 p x(p>0)$.
a) Khi 1 đơn vị đo trong mặt phẳng tọa độ ứng với $1 \mathrm{~m}$ trên thực tế, ta có $B(20 ; 200)$.
Thay tọa độ điểm $\mathrm{B}$ vào phương trình của ( $\mathrm{P})$ ta được:
$200^2=2 p .20 \Leftrightarrow p=1000$.
Vậy phương trình chính tắc của $(\mathrm{P})$ là: $y^2=2000 x$.
b) Khi 1 đơn vị đo trong mặt phẳng tọa độ ứng với $1 \mathrm{~km}$ trên thực tế, ta có $B(0,02 ; 0,2)$.
Tương tự, ta có phương trình chính tắc của $(\mathrm{P})$ là $y^2=2 x$.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Ba đường Conic Chương phương pháp tọa độ trong mặt phẳng Toán 10 Kết nối tri thức tập 2 ở các trang 48, 49, 50, 51, 52, 53, 54, 55, 56, 57. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!





