Giải SGK bài 22 trang 11, 12, 13, 14 Toán 7 Kết nối tri thức Tập 2
Trong bài viết này HocThatGioi sẽ cùng bạn đi tìm đáp án và phương pháp tốt nhất giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Đại lượng tỉ lệ thuận. Các bài tập sau đây thuộc bài 22 chương 6 – Tỉ lệ thức và đại lượng tỉ lệ ở các trang 11, 12, 13, 14 Toán 7 Kết nối tri thức tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Giải SGK mục 1 trang 11, 12 Toán 7 Kết nối tri thức Tập 2
Cùng HocThatGioi tìm ra đáp án chính xác nhất cho các câu hỏi hoạt động ở Mục 1 của các trang 11, 12 trong bài Đại lượng tỉ lệ thuận ở ngay bên dưới nhé!
Giải hoạt động 1 SGK trang 11
Thay mỗi dấu “$?$” trong bảng sau bằng số thích hợp.
| $t$ ($h$) | 1 | 1,5 | 2 | 2 |
| $s$ ($km$) | ? | ? | ? | ? |
Quãng đường = vận tốc . thời gian.
Khi $t = 1$ thì $s = v. t = 60.1 = 60$ ($km$)
Khi $t = 1,5$ thì $s = v. t = 60.1,5 = 90$ ($km$)
Khi $t = 2$ thì $s = v. t = 60.2 = 120$ ($km$)
Khi $t = 3$ thì $s = v. t = 60.3 = 180$ ($km$)
| $t$ ($h$) | 1 | 1,5 | 2 | 2 |
| $s$ ($km$) | 60 | 90 | 120 | 180 |
Giải SGK hoạt động 2 trang 11
Viết công thức tính quãng đường s theo thời gian di chuyển tương ứng t.
Quãng đường = vận tốc . thời gian.
Ta có:
$S = v .t$
Trong đó: $s$: quãng đường đi được
$v$: vận tốc di chuyển
$t$: thời gian di chuyển
Giải SGK câu hỏi trang 11
Nếu $y = a.x$ ($a$ là hằng số khác $0$) thì $y$ tỉ lệ thuận với $x$ theo hệ số tỉ lệ $a$.
Ta có: $s = v . t$. Vì $v$ không đổi nên quãng đường $s$ tỉ lệ thuận với thời gian $t$.
$t = \frac{s}{v} = \frac{1}{v}.s$. Vì $v$ không đổi nên $\frac{1}{v}$ cũng không đổi. Do đó, thời gian $t$ tỉ lệ thuận với quãng đường $s$.
$Chú$ $ý$:
Nếu $y$ tỉ lệ thuận với $x$ theo hệ số tỉ lệ $a$ thì $x$ tỉ lệ thuận với $y$ theo hệ số $\frac{1}{a}$.
Giải SGK luyện tập 1 trang 12
Nếu $y = a.x$ ($a$ là hằng số khác $0$) thì $y$ tỉ lệ thuận với $x$ theo hệ số tỉ lệ $a$.
Nếu $2$ đại lượng tỉ lệ thuận thì tỉ số $2$ giá trị tương ứng của chúng luôn không đổi.
Tỉ số khối lượng protein trong đậu tương và khối lượng đậu tương luôn không đổi nên khối lượng protein trong đậu tương có tỉ lệ thuận với khối lượng đậu tương.
Hệ số tỉ lệ là: $\frac{34}{100}=0,34$.
Giải vận dụng SGK trang 12
Bột sắn dây được làm từ củ sắn dây, là một loại thực phẩm có nhiều tác dụng tốt với sức khỏe. Ông An nhận thấy cứ $4,5$ $kg$ củ sắn dây tươi thì thu được khoảng $1$ $kg$ bột. Hỏi với $3$ tạ củ sắn dây tươi, ông An sẽ thu được khoảng bao nhiêu kilôgam bột sắn dây?
Nếu $y = a.x$ ($a$ là hằng số khác $0$) thì $y$ tỉ lệ thuận với $x$ theo hệ số tỉ lệ $a$.
Nếu $2$ đại lượng tỉ lệ thuận thì tỉ số $2$ giá trị tương ứng của chúng luôn không đổi.
Gọi khối lượng bột sắn dây ông An thu được từ $3$ $tạ$ $= 300$ $kg$ củ sắn dây tươi là $x$ ($kg$) ($x > 0$)
Vì tỉ số khối lượng bột sắn dây và khối lượng củ sắn dây tươi luôn không đổi nên khối lượng bột sắn dây và khối lượng củ sắn dây tươi là hai đại lượng tỉ lệ thuận
Áp dụng tính chất của hai đại lượng tỉ lê thuận, ta có:
$\frac{1}{4,5}=\frac{x}{300}\Rightarrow x=\frac{1.300}{4,5} = 66,(6)$
Vậy ông An thu được khoảng $66,6$ $kg$ bột sắn dây.
Giải SGK mục 2 trang 13, 14 Toán 7 Kết nối tri thức tập 2
Bài viết giải SGK Bài 22 Đại lượng tỉ lệ thuận đang dần đi đến hồi kết. Hãy cùng HocThatGioi tìm ra đáp án chính xác nhất cho các hoạt động và các câu hỏi luyện tập, ở các trang 13, 14 ở ngay bên dưới nhé!
Giải SGK luyện tập 2 trang 13
+ Khối lượng của một vật đồng chất tỉ lệ thuận với thể tích của nó.
+ Sử dụng tính chất của hai đại lượng tỉ lệ thuận: tỉ số $2$ giá trị tương ứng của chúng luôn không đổi
+ Áp dụng tính chất của dãy tỉ số bằng nhau: $\frac{a}{b}=\frac{c}{d}=\frac{a-c}{b-d}$
Gọi khối lượng của mỗi thanh là $x, y$ ($g$) ($x,y > 0$)
Vì khối lượng của một vật đồng chất tỉ lệ thuận với thể tích của nó nên $\frac{x}{10}=\frac{y}{15}$ (tính chất $2$ đại lượng tỉ lệ thuận)
Ta thấy, $x < y$ nên theo đề bài, ta có $y – x = 40$.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
$\frac{y}{15}=\frac{x}{10}=\frac{y-x}{15-10}=\frac{40}{5}=8$
$\Rightarrow y=8.15=120$
$x=8.10=80$
Vậy $2$ thanh nặng lần lượt là $80$ $g$ và $120$ $g$.
Giải SGK luyện tập 3 trang 14
Gọi khối lượng $3$ phần lần lượt là $x,y,z$ ($kg$) ($x,y,z > 0$)
Sử dụng tính chất của dãy tỉ số bằng nhau:
$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{a+c+e}{b+d+f}$
Gọi khối lượng $3$ phần lần lượt là $x,y,z$ ($kg$) ($x,y,z > 0$)
Vì tổng $3$ phần là $1$ $tấn$ $=$ $1000$ $kg$ nên $x+y+z = 1000$
Vì $3$ phần có khối lượng tỉ lệ thuận với $2;3;5$ nên $\frac{x}{2}=\frac{y}{3}=\frac{z}{5}$.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
$\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=\frac{x+y+z}{2+3+5}=\frac{1000}{10}=100$
$\Rightarrow x=100.2=200$
$y=100.3=300$
$z=100.5=500$
Vậy $3$ phần cần chia có khối lượng lần lượt là $200$ $kg$, $300$ $kg$, $500$ $kg$.
Giải SGK bài tập trang 14 Toán 7 Kết nối tri thức Tập 2
Tạm khép lại phần lý thuyết của bài Đại lượng tỉ lệ thuận. Chúng ta hãy cùng nhau giải các bài tập trong bài Đại lượng tỉ lệ thuận, ở trang 14 SGK Toán 7 Kết nối tri thức Tập 2 ngay nhé.
Giải SGK bài 6.17 trang 14
Viết công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng $x$ và $y$.
| x | 2 | 4 | 5 | ? | ? | ? |
| y | -6 | ? | ? | 9 | 18 | 1,5 |
Sử dụng tính chất của hai đại lượng tỉ lệ thuận: $\frac{x_{1}}{y_{1}}= \frac{x_{2}}{y_{2}}=\frac{x_{3}}{y_{3}}=…=k$. Công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng $x$ và $y$ là: $y=k.x$
Vì x và y là hai đại lượng tỉ lệ thuận, có $\frac{y_{1}}{x_{1}}= \frac{-6}{2}=-3$ nên ta có công thức liên hệ: $y= -3.x$
| x | 2 | 4 | 5 | -3 | -6 | -0,5 |
| y | -6 | -12 | -15 | 9 | 18 | 1,5 |
Giải SGK bài 6.18 trang 14
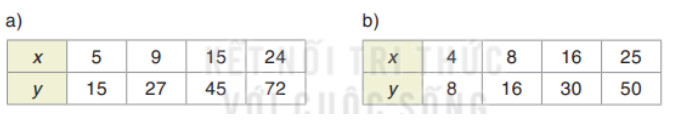
Kiểm tra tỉ số $2$ giá trị tương ứng của chúng có luôn bằng nhau không.
+ Nếu bằng thì $2$ đại lượng đó tỉ lệ thuận.
+ Nếu không bằng thì $2$ đại lượng đó không là hai địa lượng tỉ lệ thuận.
a) Ta có: $\frac{5}{15}=\frac{9}{27}=\frac{15}{45}=\frac{24}{72}$ nên $2$ đại lượng $x, y$ là hai đại lượng tỉ lệ thuận.
b) Ta có: $\frac{4}{8}=\frac{8}{16}=\frac{25}{50}\neq \frac{24}{72}$ nên $2$ đại lượng $x, y$ không là hai đại lượng tỉ lệ thuận.
Giải SGK bài 6.19 trang 14
+ Sử dụng định nghĩa $2$ đại lượng tỉ lệ thuận:
Nếu $y = a.x$ ($a$ là hằng số khác $0$) thì $y$ tỉ lệ thuận với $x$ theo hệ số tỉ lệ $a$.
+ Biểu diễn đại lượng $y$ theo $z$. Nếu $y = k. z$ ( $k$ là hằng số) thì $y$ và $z$ là hai đại lượng tỉ lệ thuận.
Vì $y$ tỉ lệ thuận với $x$ theo hệ số tỉ lệ $a$ nên $y = a.x$.
Vì $x$ tỉ lệ thuận với $z$ theo hệ số tỉ lệ $b$ nên $x = b.z$.
Do đó, $y = a.x = a.(b.z ) = (a.b).z$ ( $a.b$ là hằng số vì $a,b$ là các hằng số)
Vậy y có tỉ lệ thuận với $z$ và hệ số tỉ lệ là $a.b$.
Giải SGK bài 6.20 trang 14
Chiều cao bể nước và thời gian đầy bể là hai đại lượng tỉ lệ thuận
Áp dụng tính chất của hai đại lượng tỉ lệ thuận: $\frac{x_{1}}{x_{2}} = \frac{y_{1}}{y_{2}}$.
Gọi thời gian để bơm đầy nước vào bể thứ hai là $x$ (giờ) ($x > 0$)
Vì $2$ bể nước hình hộp chữ nhật có chiều dài và chiều rộng tương ứng bằng nhau và máy bơm có cùng công suất nên chiều cao bể nước và thời gian đầy bể là hai đại lượng tỉ lệ thuận.
Áp dụng tính chất của hai đại lượng tỉ lệ thuận, ta có:
$\frac{3}{4}=\frac{4,5}{x}\Rightarrow x=\frac{4.4,5}{3}=6$ (thỏa mãn)
Vậy thời gian để bơm đầy nước vào bể thứ hai là $6$ giờ.
Giải SGK bài 6.21 trang 14
Gọi thể tích $3$ phần lần lượt là $x,y,z$ (lít) ($x,y,z > 0$)
Sử dụng tính chất của dãy tỉ số bằng nhau:
$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{a+c+e}{b+d+f}$
Gọi thể tích $3$ phần lần lượt là $x,y,z$ $(lít)$ $(x,y,z>0)$.
Vì cô Hương chia $1,5$ lít hóa chất thành ba phần nên: $x+y+z=1,5$.
Vì ba phần tỉ lệ thuận với $4;5;6$ nên $\frac{x}{4}=\frac{y}{5}=\frac{z}{6}$.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
$\frac{x}{4}=\frac{y}{5}=\frac{z}{6}= \frac{x+y+z}{4+5+6}=\frac{1,5}{15}=0,1$
$\Rightarrow $ $x=0,1.4=0,4$
$y=0,1.5=0,5$
$z=0,1.6=0,6$
Vậy $3$ chiếc lọ đựng lần lượt là $0,4$ lít, $0,5$ lít, $0,6$ lít hóa chất.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Bài viết này đã giải quyết tất cả các bài tập, câu hỏi, các hoạt động của bài 31- Đại lượng tỉ lệ thuận, chương 6 trang 11, 12, 13, 14 Toán 7 Kết nối tri thức Tập 2. Chúc các bạn học tốt và tiếp thu được nhiều kiến thức bổ ích nhé!





