Giải SGK bài 28 Phép chia đa thức một biến Toán 7 Kết nối tri thức Tập 2
Ở bài viết này, HocThatGioi sẽ cùng bạn giải quyết tất cả những câu hỏi khởi động, vận dụng, bài tập trong bài Phép chia đa thức một biến. Các bài tập sau đây thuộc bài 28 chương 7 trang 39, 40, 41, 42, 43 Toán 7 Kết Nối Tri Thức Tập 2. Hy vọng, sau bài viết này các bạn có thể nắm vững tất cả các kiến thức đã học, và có thể áp dụng chúng để giải tất cả bài tập một cách dễ dàng theo những lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Giải SGK mục 1 trang 39, 40 Toán 7 Kết nối tri thức Tập 2
Dưới đây là phương pháp cụ thể và bài giải chi tiết, dễ hiểu cho các câu hỏi hoạt động, thực hành cùng phần luyện tập ở các trang 39, 40 SGK Toán 7 Kết nối tri thức Tập 2. Cùng HocThatGioi đi tìm đáp án và phương pháp giải hay nhất ngay nhé!
Giải SGK hoạt động 1 trang 40
a) $12x^{3} : 4x$
b) $(-2x^{4} ) : x^{4}$
c) $2x^{5} : 5x^{2}$
Bước $1$: Chia $2$ hệ số
Bước $2$: Chia $2$ lũy thừa của biến
Bước $3$: Nhân $2$ kết quả trên, ta được thương
a) $12x^{3} : 4x = (12:4) . (x^{3} : x) = 3.x^{2}$
b) $(-2x^{4} ) : x^{4} = [(-2) : 1] . (x^{4} : x^{4}) = -2$
c) $2x^{5} : 5x^{2} = (2:5) . (x^{5} : x^{2}) = \frac{2}{5}x^{3}$
Giải SGK hoạt động 2 trang 40
a) Với điều kiện nào (của hai số mũ) thì thương hai lũy thừa của $x$ cũng là một lũy thừa của $x$ với số mũ nguyên dương?
b) Thương hai lũy thừa của $x$ cùng bậc bằng bao nhiêu?
$x^{m}:x^{n}=x^{m-n}$
a) Do $x^{m}:x^{n}=x^{m-n}$ của $x$ cũng là một lũy thừa của $x$ với số mũ nguyên dương, tức là $m – n > 0$ thì $m > n$
b) Ta có: $x^{m}:x^{n}=x^{m-n}$ $=x^{0} =1$
Vậy thương hai lũy thừa của x cùng bậc bằng $1$
Giải SGK luyện tập 1 trang 40
a) $3x^{7} :12x^{4}$;
b) $(−2x):x$
c) $0,25x^{5} :(−5x^{2})$
Bước $1$: Chia $2$ hệ số
Bước $2$: Chia $2$ lũy thừa của biến
Bước $3$: Nhân $2$ kết quả trên, ta được thương
a) $3x^{7} :12x^{4} =(3:12).(x^{7} : x^{4}) = 6x^{3}$
b) $(−2x) : x =[(−2):1].(x:x)=−2$
c) $0,25x^{5} : (−5x^{2}) = [0,25:(−5)].(x^{5} : x^{2})=−0,05.x^{3}$
Giải SGK mục 2 trang 40, 41 Toán 7 Kết nối tri thức Tập 2
Sau đây, hãy cùng HocThatGioi tìm ra đáp án chính xác nhất cho các câu hỏi, các câu hỏi luyện tập và vận dụng. Ở các trang 40, 41 trong bài Phép chia đa thức một biến ở ngay bên dưới nhé!
Giải SGK câu hỏi trang 41
Nhân đa thức $B$ với đa thức $2x^{2} – 5x + 1$. Nếu kết quả bằng đa thức $A$ thì đúng
Ta có: $B . (2x^{2} – 5x + 1)$
$= (x^{2} – 4x – 3) . (2x^{2} – 5x + 1)$
$= x^{2} .(2x^{2} – 5x + 1) – 4x . (2x^{2} – 5x + 1) – 3.(2x^{2} – 5x + 1)$
$= x^{2} . 2x^{2} + x^{2} . (-5x) + x^{2} . 1 – [4x . 2x^{2} + 4x . (-5x) + 4x . 1] – [3.2x^{2} + 3.(-5x) + 3.1]$
$= 2x^{4} – 5x^{3} + x^{2} – ( 8x^{3} – 20x^{2} + 4x) – (6x^{2} – 15x + 3)$
$= 2x^{4} – 5x^{3} + x^{2} – 8x^{3} + 20x^{2} – 4x – 6x^{2} + 15x – 3$
$= 2x^{4} + (-5x^{3} – 8x^{3}) + (x^{2} + 20x^{2} – 6x^{2} ) + (-4x + 15x) – 3$
$= 2x^{4} – 13x^{3} + 15×2^{2}$
Vậy ta có phép chia hết $A : B = 2x^{2} – 5x + 1$
Giải SGK Luyện tập 2 trang 41
a) $(-x^{6} + 5x^{4} – 2x^{3}) : (0,5x^{2})$
b) $(9x^{2} – 4) : (3x + 2)$
Muốn chia đa thức $A$ cho đa thức $B$, ta làm như sau:
Bước $1$: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của $A$ chia cho hạng tử bậc cao nhất của $B$.
Bước $2$: Lấy $A$ trừ đi tích của $B$ với thương mới thu được ở bước $1$
Bước $3$: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của $B$
Bước $4$: Lấy dư thứ nhất trừ đi tích $B$ với thương vừa thu được ở bước $3$
Bước $5$: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của $B$ thì quá trình chia kết thúc.
a) $(-x^{6} + 5x^{4} – 2x^{3}) : (0,5x^{2})$
$= (-x^{6} : 0,5x^{2}) + (5x^{4} : 0,5x^{2}) + (-2x^{3} : 0,5x^{2})$
$= -2x^{4} + 10x^{2} – 4x$
Bước $1$. Lấy hạng tử có bậc cao nhất của đa thức 9x^{2} – 4 chia cho hạng tử có bậc cao nhất của đa thức $3x + 2:9x^{2} : 3x = 3x$.
Bước $2$. Lấy đa thức 9x^{2} – 4 trừ đi $(3x + 2).3x$ ta được dư thứ nhất là $-6x – 4$.
Bước $3$. Lấy hạng tử có bậc cao nhất của dư thứ nhất chia cho hạng tử có bậc cao nhất của đa thức $3x + 2: -6x : 3x = -2$.
Bước $4$. Lấy dư thứ nhất trừ đi $-2(3x + 2$) ta được dư thứ hai là $0$ nên quá trình chia kết thúc.
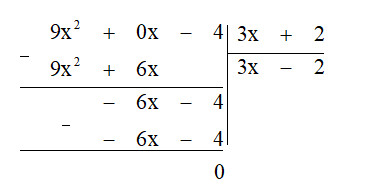
Vậy $(9x^{2} – 4) : (3x + 2) = 3x – 2$.
Giải SGK vận dụng trang 41
Tìm đa thức $P$ sao cho $A = B. P$, trong đó $A = 2x^{4} – 3x^{3} – 3x^{2} + 6x – 2$ và $B = x^{2} – 2$
+) $P = A : B$
+) Muốn chia đa thức $A$ cho đa thức $B$, ta làm như sau:
Bước $1$: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của $A$ chia cho hạng tử bậc cao nhất của $B$.
Bước $2$: Lấy $A$ trừ đi tích của $B$ với thương mới thu được ở bước $1$.
Bước $3$: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của $B$.
Bước $4$: Lấy dư thứ nhất trừ đi tích $B$ với thương vừa thu được ở bước $3$.
Bước $5$: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của $B$ thì quá trình chia kết thúc.
Bước $1$. Lấy hạng tử có bậc cao nhất của $A$ chia cho hạng tử có bậc cao nhất của $B$:
$2x^{4} : x^{2} = 2x^{2}$.
Bước $2$. Lấy A trừ đi tích $B$. $2x^{2}$ ta được dư thứ nhất là $-3x^{3} + x^{2} + 6x – 2$.
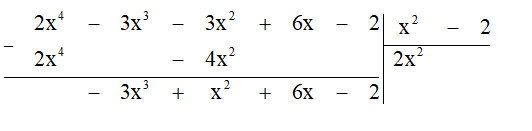
$(-3x^{3}) : x^{2} = -3x$.
Bước $4$. Lấy dư thứ nhất trừ đi tích $B$. $(-3x)$ ta được dư thứ hai là $x^{2} – 2$.
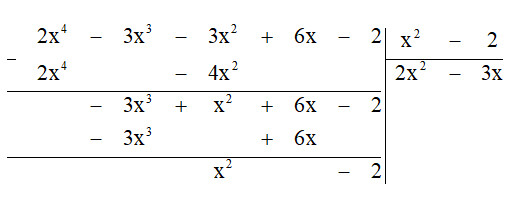
$x^{2} : x^{2} = 1$.
Bước $6$. Lấy dư thứ nhất trừ đi tích $B$. $1$ ta được dư thứ ba là $0$.
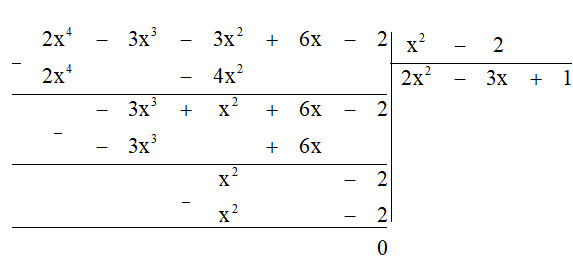
Bước $7$. Dư cuối cùng bằng $0$ nên quá trình chia kết thúc.
Vậy $A : B = 2x^{2} – 3x + 1$.
Giải SGK mục 3 trang 42 Toán 7 Kết nối tri thức Tập 2
Sau đây, hãy cùng HocThatGioi tìm ra đáp án chính xác nhất cho các hoạt động và các câu hỏi luyện tập ở các trang 42 trong bài Phép chia đa thức một biến ở ngay bên dưới nhé!
Giải SGK hoạt động 3 trang 42
Mô tả lại các bước tương tự như chia đa thức cho đa thức trường hợp chia hết.
Bước $1$: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của $D$ chia cho hạng tử bậc cao nhất của $E$.
Bước $2$: Lấy $D$ trừ đi tích của $E$ với thương mới thu được ở bước $1$
Bước $3$: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của $E$
Bước $4$: Lấy dư thứ nhất trừ đi tích $E$ với thương vừa thu được ở bước $3$. Ta được dư thứ hai có bậc nhỏ hơn bậc của $E$ thì quá trình chia kết thúc.
Giải SGK hoạt động 4 trang 42
Đa thức bậc $n$ không chia được cho đa thức bậc $m (n < m)$.
Lúc này phép chia không thực hiện được nữa vì bậc của đa thức $-6x + 10$ (là $1$) nhỏ hơn bậc của đa thức chia $x^{2} + 1$ (là $2$)
Giải SGK hoạt động 5 trang 42
Bước $1$: Thực hiện phép nhân đa thức $E .(5x – 3)$
Bước $2$: Thực hiện phép cộng đa thức tìm được ở bước $1$ với đa thức $G$.
Nếu kết quả = đa thức $D$ thì đúng
Ta có: $E . (5x – 3) + G$
$= (x^{2} + 1) . (5x – 3) + (-6x + 10)$
$= x^{2} .(5x – 3) + 1. (5x – 3) + (-6x) + 10$
$= x^{2} . 5x + x^{2} . (-3) + 5x – 3 – 6x + 10$
$= 5x^{3} – 3x^{2} + (5x – 6x) + (-3 + 10)$
$= 5x^{3} – 3x^{2} – x + 7$
$= D$
Vậy đẳng thức đúng.
Giải SGK luyện tập 3 trang 42
+) Muốn chia đa thức $A$ cho đa thức $B$, ta làm như sau:
Bước $1$: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của $A$ chia cho hạng tử bậc cao nhất của $B$.
Bước $2$: Lấy $A$ trừ đi tích của $B$ với thương mới thu được ở bước $1$.
Bước $3$: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của $B$.
Bước $4$: Lấy dư thứ nhất trừ đi tích $B$ với thương vừa thu được ở bước $3$.
Bước $5$: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của $B$ thì quá trình chia kết thúc.
+) Viết $A = B. Q + R$
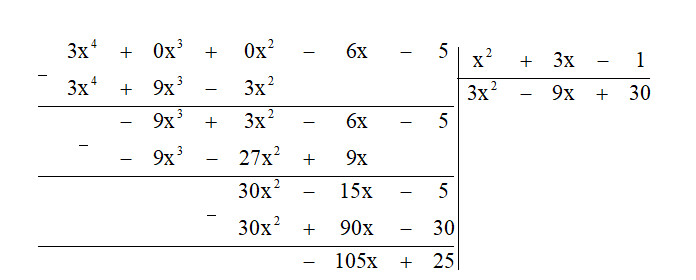
Giải SGK thử thách nhỏ trang 42

Xét phép chia $(A + B) : C$ với bậc của $B$ nhỏ hơn bậc của $C$
Nếu $A$ chia $C$ không dư thì số dư của $(A + B ) : C$ là $B$.
Ta có: $x^{3} – 3x^{2} + x – 1 = (x^{3} – 3x^{2} ) + (x -1$).
Vì $x^{3} – 3x^{2}$ chia cho $x^{2} – 3x$ không dư ; bậc của $x – 1$ nhỏ hơn bậc của $x^{2} – 3x$ nên số dư của phép chia $(x^{3} – 3x^{2} ) + (x -1)$ cho $x^{2} – 3x$ là $x – 1$
Vậy Vuông làm nhanh và đúng.
Giải SGK bài tập trang 43 Toán 7 Kết nối tri thức Tập 2
Hãy cùng HocThatGioi ôn tập lại các kiến thức cũ và áp dụng các lý thuyết, công thức, định lý,… đã học để giải các bài tập trong bài 28 ở trang 43 SGK Toán 7 Kết nối tri thức tập 2.
Giải SGK bài 7.30 trang 43
a) $8x^{5} : 4x^{3}$
b) $120x^{7} : (-24x^{5})$
c) $\frac{3}{4}(−x)^{3} : \frac{1}{8}x$
d) $-3,72x^{4} : (-4x^{2})$
Bước $1$: Chia $2$ hệ số
Bước $2$: Chia $2$ lũy thừa của biến
Bước $3$: Nhân $2$ kết quả trên, ta được thương
a) $8x^{5} : 4x^{3} = (8 : 4) . (x^{5} : x^{3}) = 2.x^{2}$
b) $120x^{7} : (-24x^{5}) = [120 : (-24)] . (x^{7} : x^{5}) = -5.x^{2}$
c) $\frac{3}{4}(−x)^{3}:\frac{1}{8}x=−\frac{3}{4}x^{3}:\frac{1}{8}x=(−\frac{3}{4}:\frac{1}{8}).(x^{3}:x)=−6x^{2}$
d) $-3,72x^{4} : (-4x^{2}) = [(-3,72) : (-4)] . (x^{4} : x^{2}) = 0,93x^{2}$
Giải SGK bài 7.31 trang 43
a) $(-5x^{3} + 15x^{2} + 18x) : (-5x)$
b) $(-2x^{5} – 4x^{3} + 3x^{2}) : 2x^{2}$
Muốn chia đa thức cho đơn thức, ta chia từng hạng tử của đa thức cho đơn thức rồi tổng các kết quả thu được.
a) $(-5x^{3} + 15x^{3} + 18x) : (-5x)$
$= (-5x^{3}) : (-5x) + 15x^{2} : (-5x) + 18x : (-5x)$
$= [(-5): (-5)] . (x^{3} : x) + [15 : (-5)] . (x^{2} : x) + [18 : (-5)]. (x : x)$
$= x^{2} – 3x – \frac{15}{8}$
b) $(-2x^{5} – 4x^{3} + 3x^{2}) : 2x^{2}$
$= (-2x^{5} : 2x^{2}) + (-4x^{3} : 2x^{2}) + (3x^{2} : 2x^{2})$
$= [(-2) : 2] . (x^{5} : x^{2}) + [(-4) : 2] . (x^{3} : x^{2}) + (3 : 2) . (x^{2} : x^{2})$
$= -x^{3} – 2x + \frac{3}{2}$
Giải SGK bài 7.32 trang 43
a) $(6x^{3} – 2x^{2} – 9x + 3) : (3x – 1)$
b) $(4x^{4} + 14x^{3} – 21x – 9) : (2x^{2} – 3)$
+) Muốn chia đa thức $A$ cho đa thức $B$, ta làm như sau:
Bước $1$: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của $A$ chia cho hạng tử bậc cao nhất của $B$.
Bước $2$: Lấy $A$ trừ đi tích của $B$ với thương mới thu được ở bước $1$
Bước $3$: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của $B$
Bước $4$: Lấy dư thứ nhất trừ đi tích $B$ với thương vừa thu được ở bước $3$
Bước $5$: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của $B$ thì quá trình chia kết thúc.
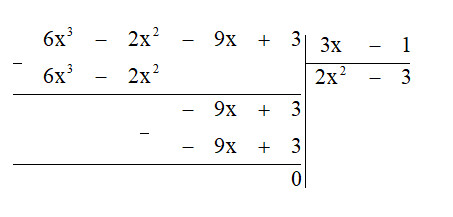
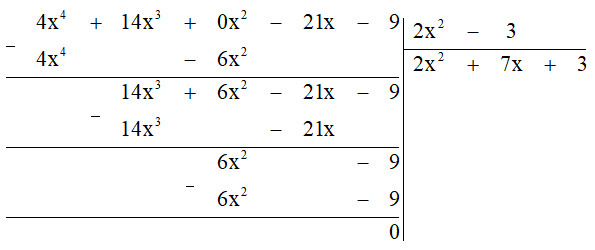
Giải SGK bài 7.33 trang 43
a) $n = 2$
b) $n = 3$
Muốn chia đa thức cho đơn thức, ta chia từng hạng tử của đa thức cho đơn thức rồi tổng các kết quả thu được.
a) $(0,5x^{5} + 3,2x^{3} – 2x^{2} ) : 0,25x^{2}$
$= 0,5x^{5} : 0,25x^{2} + 3,2x^{3} : 0,25x^{2} – 2x^{2} : 0,25x^{2}$
$= (0,5:0,25).(x^{5} : x^{2}) + (3,2 : 0,25). (x^{3} : x^{2} ) – (2 : 0,25). (x^{2} : x^{2})$
$= 2x^{3} + 12,8x – 8$

Giải SGK bài 7.34 trang 43
$F(x) = G(x) . Q(x) + R(x)$
a) $F(x) = 6x^{4} – 3x^{3} + 15x^{2} + 2x – 1$ ; $G(x) = 3x^{2}$
b) $F(x) = 12x^{4} + 10x^{3} – x – 3$ ; $G(x) = 3x^{2} + x + 1$
+) Muốn chia đa thức $A$ cho đa thức $B$, ta làm như sau:
Bước $1$: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của $A$ chia cho hạng tử bậc cao nhất của $B$.
Bước $2$: Lấy $A$ trừ đi tích của $B$ với thương mới thu được ở bước $1$
Bước $3$: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của $B$
Bước $4$: Lấy dư thứ nhất trừ đi tích $B$ với thương vừa thu được ở bước $3$
Bước $5$: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của $B$ thì quá trình chia kết thúc.
+) Viết $A = B. Q + R$
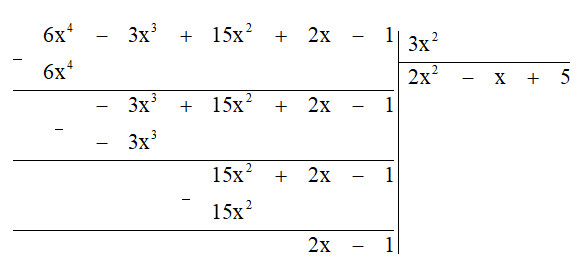
Do đó $Q(x) = 2x^{2} – x + 5$; $R(x) = 2x – 1$.
Vậy $6x^{4} – 3x^{3} + 15x^{2} + 2x – 1 = 3x^{2} . (2x^{2} – x + 5) + 2x – 1$.

Do đó $Q(x) = 4x^{2} + 2x – 2$; $R(x) = -x – 1$.
Vậy $12x^{4} + 10x^{3} – x – 3 = (3x^{2} + x + 1) . (4x^{2} + 2x – 2) – x – 1$.
Giải SGK bài 7.35 trang 43
Khi đa thức bị chia có bậc nhỏ hơn bậc của đa thức chia thì thương là $0$, số dư là đa thức chia.
Ta thấy bậc của đa thức bị chia $21x – 4$ là $1$, bậc của đa thức chia $3x^{2}$ là $2$.
Do $1 < 2$ nên không thể thực hiện được phép chia.
Do đó thương của phép chia bằng $0$ và dư của phép chia là $21x – 4$.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Bài viết này đã giải quyết tất cả các bài tập, câu hỏi, các hoạt động của bài Phép chia đa thức một biến. Các bài tập sau đây thuộc Bài 28 chương 7 trang 39, 40, 41, 42, 43 Toán 7 Kết nối tri thức Tập 2. Hy vọng, qua bài viết này bạn có thể nắm rõ tất cả các kiến thức và giải tất cả các bài tập một cách tốt nhất. Chúc các bạn có một buổi học thật thú vị nhé!





