Giải SGK bài 33 trang 66, 67, 68, 69 Chương 9 Toán 7 Kết nối tri thức tập 2
Trong bài viết này HocThatGioi sẽ cùng bạn đi tìm đáp án và phương pháp tốt nhất giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Quan hệ giữa ba cạnh của một tam giác. Các bài tập sau đây thuộc bài 33 chương 9 – Quan hệ giữa ba cạnh của một tam giác ở các trang 66, 67, 68, 69 Toán 7 Kết nối tri thức tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Giải câu hỏi trang 66, 67, 68 SGK toan 7 Kết nối tri thức tập 2
Dưới đây sẽ làm rõ các phần lý thuyết và tổng hợp những phương pháp, cách giải chi tiết cho các câu hỏi hoạt động, hoạt động khám phá, luyện tập cùng phần vận dụng ở các trang 66, 67, 68 trong bài Quan hệ giữa ba cạnh của một tam giác Cùng HocThatGioi đi tìm đáp án ngay nhé!
Giải hoạt động 1 SGK trang 66
Bộ thứ nhất: $10 cm, 20 cm, 25 cm$.
Bộ thứ hai: $5 cm, 15 cm, 25 cm$.
Em hãy ghép và cho biết bộ nào ghép được thành một tam giác.
Ghép sao cho cứ $2$ đầu của $2$ thanh tre trùng nhau thì bộ ba đó ghép được thành tam giác.
Bộ thứ nhất ghép được thành tam giác.
Giải hoạt động 2 SGK trang 66
Tính tổng độ dài của $2$ thanh tre bất kì rồi so sánh với độ dài thanh còn lại.
Ta có: $10 + 20 = 30 > 25$
$10 + 25 = 35 > 20$
$20 + 25 = 45 > 10$
Vậy độ dài của thanh tre bất kì luôn nhỏ hơn tổng độ dài $2$ thanh còn lại.
Giải tranh luận SGK trang 67

Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại.
Kiểm tra, nếu ba độ dài không thỏa mãn bất đẳng thức tam giác thì chúng không ghép được thành một tam giác.
Vì $1+ 2 < 4$ nên bộ ba đoạn thẳng không lập được thành $1$ tam giác.
Vậy Vuông sai, Tròn đúng.
$Chú$ $ý$: Khi kiểm tra $3$ đoạn thẳng có thỏa mãn bất đẳng thức tam giác không, để nhanh gọn, ta chỉ cần kiểm tra tổng độ dài của $2$ cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất hay không
Giải luyện tập SGK trang 68
a) $5 cm, 4 cm, 6 cm$.
b) $3 cm, 6 cm, 10 cm$.
Khi kiểm tra $3$ đoạn thẳng có thỏa mãn bất đẳng thức tam giác không, để nhanh gọn, ta chỉ cần kiểm tra tổng độ dài của $2$ cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất hay không
Dùng thước và compa ta vẽ được hình như sau:
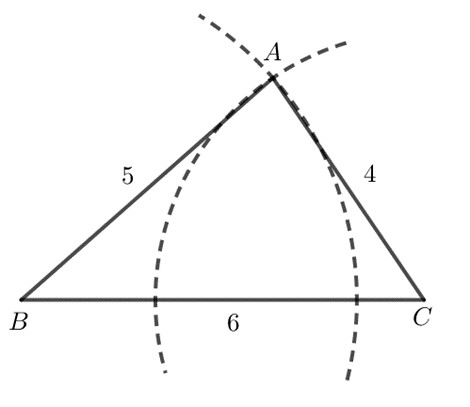
b) Vì $3 + 6 = 9 < 10$ nên ba độ dài $3 cm$, $6 cm$, $10 cm$ không thể là độ dài ba cạnh của một tam giác
Giải vận dụng SGK trang 68
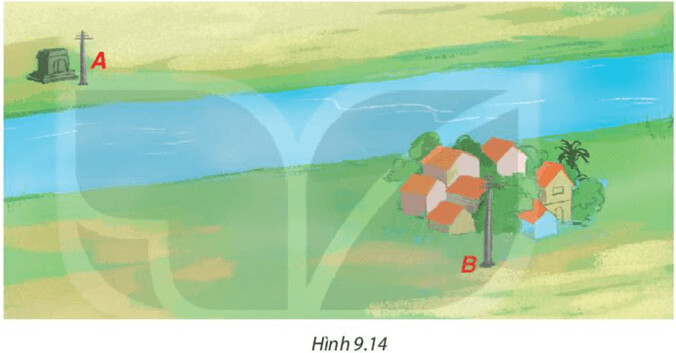
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại.
+) Nếu $A,B,C$ không thẳng hàng thì ta lập được tam giác $ABC$. Khi đó, theo bất đẳng thức tam giác, ta có:
$AC + CB > AB$, tức là độ dài dây dẫn luôn lớn hơn $AB$.
+) Nếu $A,B,C$ thẳng hàng thì $C$ nằm giữa $A$ và $B$ nên $AC + CB = AB$, tức là độ dài dây dẫn bằng $AB$.
Vậy khi $C$ nằm trên đoạn thẳng $AB$ thì tổng độ dài dây dẫn điện cần sử dụng là ngắn nhất.
Giải bài tập SGK trang 69 Toán 7 Kết nối tri thức Tập 2
Ở phần này, chúng ta hãy áp dụng những kiến thức lý thuyết ở phần 1. Để đi tìm phương pháp và đáp án chi tiết nhất cho các bài tập trong SGK bài Quan hệ giữa ba cạnh của một tam giác 69 SGK Toán 7 Kết nối tri thức Tập 2 dưới đây nhé!
Giải bài 9.10 SGK trang 69
a) $2 cm, 3 cm, 5 cm$.
b) $3 cm, 4 cm, 6 cm$.
c) $2 cm, 4 cm, 5 cm$.
Hỏi bộ ba nào không thể là độ dài ba cạnh của một tam giác? Vì sao? Với mỗi bộ ba còn lại, hãy vẽ một tam giác có độ dài ba cạnh được cho trong bộ ba đó.
Khi kiểm tra $3$ đoạn thẳng có thỏa mãn bất đẳng thức tam giác không, để nhanh gọn, ta chỉ cần kiểm tra tổng độ dài của $2$ cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất hay không.
a) Ta có $2 + 3 = 5$ nên bộ ba đoạn thẳng có độ dài $2 cm, 3 cm, 5 cm$ không phải độ dài ba cạnh của tam giác.
Sử dụng thước thẳng và compa, ta có hình như sau:
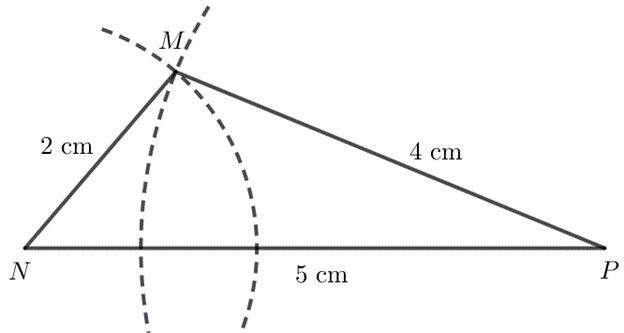
Sử dụng thước thẳng và compa, ta có hình như sau:

Giải bài 9.11 SGK trang 69
b) Cho tam giác $ABC$ có $AB= 2 cm$, $BC = 6 cm$ và $BC$ là cạnh lớn nhất. Hãy tìm độ dài cạnh $CA$ biết rằng đó là một số nguyên $(cm)$.
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài $2$ cạnh còn lại: $b – c < a < b + c$ ( với $a, b, c$ là độ dài $3$ cạnh của tam giác)
Kết hợp điều kiện độ dài cạnh $CA$ là số nguyên
Áp dụng bất đẳng thức tam giác trong tam giác $ABC$, ta có:
$7 – 1 < CA < 7 + 1$
$6 < CA BC$
$2 + CA > 6$
$CA > 4 cm$
Mà $CA$ là số nguyên và $CA < 6$ (vì $BC = 6 cm$ là cạnh lớn nhất của tam giác)
$CA = 5 cm$
Vậy $CA = 5 cm$.
Giải bài 9.12 SGK trang 69
a) So sánh $MB$ với $MN$ + $NB$, từ đó suy ra $MA$ + $MB < NA$ $+ NB$
b) So sánh $NA$ với $CA + CN$, từ đó suy ra $NA + NB < CA + CB$.
c) Chứng minh $MA + MB < CA + CB$.
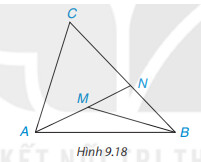
Sử dụng định lí:
+ Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.
+ Trong một tam giác, cạnh đối diện với góc lớn nhất là cạnh lớn nhất.
a) $3$ điểm $M,N,B$ không thẳng hàng.
Áp dụng bất đẳng thức tam giác trong tam giác $MNB$ có:
$MB < MN + NB$
$MA + MB < MA + MN + NB$
$MA + MB < NA + NB$ ( vì $MA + MN = NA$) (1)
b) $3$ điểm $A,N,C$ không thẳng hàng.
Áp dụng bất đẳng thức tam giác trong tam giác $ACN$ có:
$NA < CA + CN$
$NA + NB < CA + CN + NB$
$NA + NB < CA + CB$ ( vì $CN + NB = CB$) (2)
c) Từ (1) và (2) ta có:
$MA + MB < NA + NB < CA + CB$
Vậy $MA + MB < CA + CB$
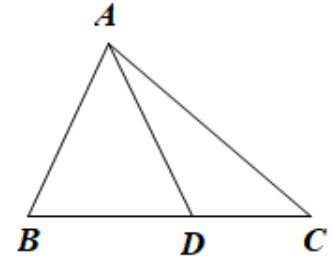
Giải bài 9.13 SGK trang 69
Áp dụng quan hệ giữa ba cạnh của tam giác $ABD$ và tam giác $ACD$.
$AD > AB + BD$ (1)
Trong tam giác $ACD$, theo bất đẳng thức tam giác ta có:
$AD > AC + CD$ (2)
Từ (1) và (2) ta có:
$AD + AD > AB + BD + AC + CD$
Do đó $2AD > AB + AC$ $+$ ($BD + CD$)
Hay $2AD > AB + AC + BC$
Suy ra $AD > \frac{1}{2}$ $(AB + AC + BC)$.
Mà chu vi tam giác $ABC$ là $AB + AC + BC$.
Nên $AD$ nhỏ hơn nửa chu vi tam giác $ABC$.
Bài học hôm nay đã đến hồi kết rồi. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Quan hệ giữa ba cạnh của một tam giác ở Chương 9 trang 66, 67, 68, 69 SGK Toán 7 Kết nối tri thức tập 2. Hy vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt.





