Giải SGK bài 7 trang 33, 34, 35, 36 Toán 7 Kết nối tri thức tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi, vận dụng, luyện tập và bài tập trong bài Tập hợp các số thực. Các bài tập sau đây thuộc Bài 7 chương 2 trang 33, 34, 35, 36 Toán 7 Kết nối tri thức. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK trang 33, 34, 35 Toán 7 Kết nối tri thức tập 1
Cùng HocThatGioi đi tìm đáp án cho các câu hỏi, luyện tập và vận dụng ở các trang 34, 35, 36 trong bài Tập hợp các số thực ở ngay bên dưới nhé!
Luyện tập 1 trang 33
b) Viết số đối của các số: $5,08(299) ;-\sqrt{5}$.
Số hữu tỉ là số viết được dưới dạng $\frac{a}{b}(a, b \in \mathbb{Z} ; b \neq 0)$
Số hữu tỉ và số vô tỉ được gọi chung là số thực
Số đối của số thực $a$ là $-a$
a) Ta có: $\sqrt{2} \notin \mathbb{Q} ; \pi \in \mathbb{I} ; 15 \in \mathbb{R}$
Vậy cách viết $\pi \in \mathbb{I} ; 15 \in \mathbb{Q}$ là đúng
b) Số đối của $5,08(299)$ là $-5,08(299)$
Số đối của – $\sqrt{5}$ là $\sqrt{5}$
Câu hỏi trang 34
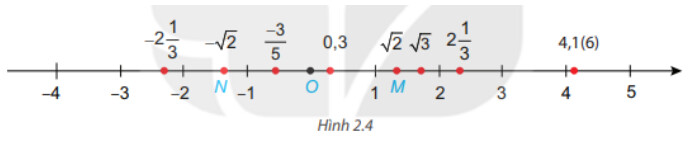
Điểm biểu diễn số $-\sqrt{2}$ là điểm $\mathrm{N}$.
Điểm biểu diễn của hai số đối nhau là 2 điểm cách đều gốc $\mathrm{O}$ và nằm về 2 phía của điểm $O$
Luyện tập 2 trang 34
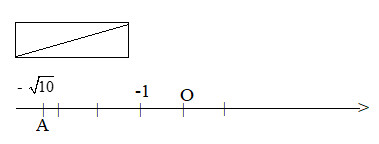
Bước 1: Vẽ tam giác vuông có hai cạnh góc vuông bằng 1 và 3 . Đo độ dài của cạnh huyền
Bước 2: Vẽ trục số. Biểu diễn số – $\sqrt{\mathbf{1 0}}$ trên trục số nằm ở bên trái gốc $\mathrm{O}$, cách $\mathrm{O}$ một khoảng bằng độ dài cạnh huyền của tam giác vuông vừa vẽ.
Luyện tập 3 trang 35
a) $1,313233 \ldots$ và $1,(32)$;
b) $\sqrt{5}$ và 2,36 (có thẻ̉ düng máy tinh cầm tay để tính $\sqrt{5}$ ).
Viết các số ở dạng số thập phân rồi so sánh các số thập phân
a) Ta có: $1,(32)=1,323232 \ldots$
Quan sát chữ số ở hàng thập phân thứ 2 , ta thấy $1<2$ nên $1,313233 \ldots<1$, (32)
b) Ta có: $\sqrt{5}=2,236 \ldots$
Quan sát chữ số ở hàng thập phân thứ nhất, ta thấy $2<3$ nên 2,236 $<2,36$
Vậy $\sqrt{5}<2,36$
Hoạt động 1 trang 35
Điểm A và B lần lượt là hai điểm biểu diễn các số 3 và –2 trên trục số.

Điểm B cách gốc O một khoảng bằng 2 đơn vị, điểm A cách gốc O một khoảng bằng 3 đơn vị.
Hoạt động 2 trang 35
Với số thực a tuỳ ý, ta có:
Khoảng cách của 1 số nguyên đến gốc O chính bằng phần số tự nhiên của số nguyên đó.
Khoảng cách của điểm -4 đến gốc O là: 4
Khoảng cách của điểm -1 đến gốc O là: 1
Khoảng cách của điểm 0 đến gốc O là: 0
Khoảng cách của điểm 1 đến gốc O là: 1
Khoảng cách của điểm 4 đến gốc O là: 4
Câu hỏi trang 35
Giá trị tuyệt đối của số a là khoảng cách của điểm a đến gốc O
Ta có: $|3|=3 ;|-2|=2 ;|0|=0 ;|4|=4 ;|-4|=4$
Câu hỏi trang 36
Minh viết $|-2,5|=-2,5$ là sai vì $|-2,5|=2,5$
Luyện tập 4 trang 36
a) $\mid-2,31$
b) $\left|\frac{7}{5}\right|$;
c) $|-11|$;
d) $|-\sqrt{8}|$
$ |a|= a$ nếu $a \geq 0$
$ |a|=-a$ nếu $ a<0$
a) $|-2,3|=2,3$;
b) $\left|\frac{7}{5}\right|=\frac{7}{5}$;
c) $|-11|=11$;
d) $|-\sqrt{8}|=\sqrt{8}$
Thử thách nhỏ trang 36
Các phần tử của tập hợp A là: $0;1; -1;2; -2 ;3; -3;4; -4.$
Giải bài tập SGK trang 36 Toán 7 Kết nối tri thức tập 1
Những bài tập SGK ở cuối bài Tập hợp các số thực trang 36 sách Toán 7 Kết nối tri thức sẽ giúp các bạn vận dụng những kiến thức vừa học để giải các bài tập từ cơ bản đến nâng cao. Cùng HocThatGioi giải quyết những bài toán này nhé!
Bài 2.13 trang 36
Bước 1: Tìm các số là số hữu tỉ; vô tỉ trong tập hợp A
+ Các số thập phân hữu hạn, vô hạn tuần hoàn là các số hữu tỉ.
+ Các số thập phân vô hạn không tuần hoàn là các số vô tỉ.
Bước 2: Mô tả tập hợp bằng cách liệt kê: Liệt kê các phần tử trong dấu { } ; mỗi phần tử được liệt kê 1 lần, thứ tự tùy ý; các phần tử ngăn cách nhau bởi dấu ;
$B=\left\{7,1 ;-2,(61) ; 0 ; 5,14 ; \frac{4}{7} ;-\sqrt{81}\right\} $
$C=\{\sqrt{15}\}$
Chú ý:
Số $-\sqrt{81}$ là số hữu tỉ vì $-\sqrt{81}=-9$
Bài 2.14 trang 36
Số đối của số thực $a$ là $-a$
Số đối của số $7,1$ là $-7,1$
Số đối của số $-2,(61)$ là $2,(61)$
Số đối của số $0$ là $0$
Số đối của số $5,14$ là $-5,14$
Số đối của số $\frac{4}{7}$ là – $\frac{4}{7}$
Số đối của số $\sqrt{15}$ là – $\sqrt{15}$
Số đối của số $-\sqrt{81}=\sqrt{81}$
Bài 2.15 trang 36
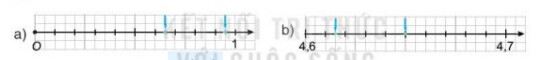
Đếm số vạch chia trên 1 đơn vị
Tìm số biểu diễn bởi mũi tên xanh
a) 1 đơn vị (từ gốc $O$ đến số 1) được chia thành 10 đoạn bằng nhau, mối đoạn đó lại được chia thành 2 đoạn nhỏ bằng nhau nên 1 đơn vị được chia thành 20 đoạn đơn vị mới có độ dài bằng nhau và bằng $\frac{1}{20}$ độ dài đoạn thẳng đơn vị cũ.
Điểm $\mathrm{A}$ nằm ở bên phải điểm $\mathrm{O}$ (nằm sau điểm $\mathrm{O}$ ) và cách $\mathrm{O}$ một khoảng bằng 13 đoạn đơn vị mới nên điểm $\mathrm{A}$ biểu diễn số $\frac{13}{20}$
Điểm $\mathrm{B}$ nằm ở bên phải điểm $\mathrm{O}$ (nằm sau điểm $\mathrm{O}$ ) và cách $\mathrm{O}$ một khoảng bằng 19 đoạn đơn vị mới nên điểm $\mathrm{B}$ biểu diễn số $\frac{19}{20}$
b) Ta có: $4,7-4,6=0,1$.
0,1 đơn vị được chia thành 20 phần bằng nhau, nên mỗi đoạn đơn vị mới bă้ng 0,005 đơn vị cũ
Điểm C nằm ở bên phải điểm 4,6 và cách điểm 4,6 một khoảng bằng 3 đoạn đơn vị mới nên điểm đó biểu diền số 4,6+3.0,005=4,615.
Điểm $D$ nằm ở bên phải điểm 4,6 và cách điểm 4,6 một khoảng bằng 10 đoạn đơn vị mới nên điểm đó biểu diền số $4,6+10.0,005=4,65$.
Bài 2.16 trang 36
a) $|-3,5|$
b) $\left|\frac{-4}{9}\right|$;
c) $|0|$
d) $12,0(3)$.
a) $|-3,5|=3,5$;
b) $\left|\frac{-4}{9}\right|=\frac{4}{9}$
c) $|0|=0$;
d) $|2,0(3)|=2,0(3)$
Nếu $a<0$ thì $|a|=-a$
Bài 2.17 trang 36
a) $a=1,25$;
b) $b=-4,1$;
c) $c=-1,414213562 \ldots$
Bước 1 : Xác định dấu của từng số
Bước 2: Nếu $a \geq 0$ thì $|a|=a$, Nếu $a<0$ thì $|a|=-a$
$a) a=1,25$ có dấu dương, $|a|=|1,25|=1,25$
$b) b=-4,1$ có dấu âm, $|b|=|-4,1|=4,1$
$c) c=-1,414213562 \ldots . $ có dấu âm, $|c|=|-1,414213562 \ldots|=1,.414213562 \ldots$.
Bài 2.18 trang 36
Các số thực $x$ thỏa mãn điều kiện $|x|=2,5$ là các số thực có khoảng cách từ số đó đến gốc tọa độ $\mathrm{O}$ là $2,5$.
Đó là 2 số $-2,5$ và $2,5$ nằm về 2 phía so với gốc $O$ và cách gốc O một khoảng $2,5$ đơn vị.
$|x|=a \Rightarrow x=a \text { hoặc } x=-a$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 7 – Tập hợp các số thực trang 33, 34, 35, 36 Toán 7 Kết nối tri thức tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





