Giải SGK bài 8 Chuyển động biến đổi. Gia tốc Vật lí 10 Kết nối tri thức
Hôm nay, ở bài 8 này, chúng ta cùng tìm hiểu về chuyển động biến đổi. Gia tốc một cách đúng nhất. Hãy tìm hiểu cách tính đúng nhất, chuẩn nhất qua bài Giải SGK bài 8 chương 2 trang 37, 38, 39 Vật lí 10 Kết nối tri thức ngay nhé.
Giải SGK mục 1 trang 37 Vật lí 10 Kết nối tri thức
Mở đầu bài học hôm nay, chúng ta cùng tìm hiểu về các chuyển động biến đổi nhé. Mục này hứa hẹn sẽ là phần lý thuyết thú vị và cần thiết đối với chúng ta. Hãy cùng đón xem nhé.
Giải SGK câu hỏi trang 37
Liên hệ thực tế.
Ví dụ về chuyển động biến đổi trong cuộc sống:
+ Máy bay đang bay trên bầu trời
+ Xe máy đang chuyển động trên đường
+ Con muỗi đang bay..
Giải SGK mục 2 Vật lí 10 Kết nối tri thức
Phần tiếp theo của bài học hôm nay, hãy cùng HocThatGioi tìm hiểu các kiến thức về gia tốc của chuyển động biến đổi. Và tìm hiểu kỹ càng hơn qua các bài tập ví dụ cụ thể nhất, chân thật nhất.
Giải SGK câu hỏi 1 trang 38
$2$. Xác định độ biến thiên của vận tốc sau mỗi giây của chuyển động trên trong $4 s$ đầu và trong $4 s$ cuối
$3$. Các đại lượng xác định được ở câu $2$ cho ta biết điều gì về sự thay đổi vận tốc của chuyển động trên?
Biểu thức độ biến thiên vận tốc: $a = \frac{\Delta v}{\Delta t}$
$1$. Bảng số liệu của chuyển động
$a = \frac{\Delta v}{\Delta t} = \frac{12,5}{8} = 1,5625 (m/s^{2})$
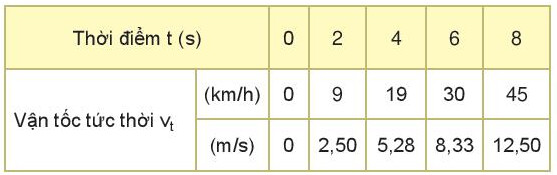
$a = \frac{\Delta v}{\Delta t} = \frac{5,28}{4} = 1,32(m/s^{2})$
+ Độ biến thiên vận tốc sau $4 s$ sau chuyển động:
$a = \frac{\Delta v}{\Delta t} = \frac{12,50 – 5,28}{4} = 1,805 (m/s^{2})$
$3$. Các đại lượng được xác định trong câu $2$ cho ta biết vận tốc của vật chuyển động tăng dần.
Giải SGK câu hỏi 2 trang 38
Gia tốc $a$ cho biết sự thay đổi nhanh chậm của vận tốc.
+ Chọn chiều dương là chiều chuyển động của vật
+ Giả sử vật chuyển động theo chiều dương nên $v >0$
+ Khi vật chuyển động nhanh dần thì vận tốc của vật cũng tăng dần, nên theo biểu thức tính gia tốc $a = \frac{\Delta v}{\Delta t}$, $\Delta v > 0$
$\Rightarrow $ $a.v>0$
+ Khi vật chuyển động chậm dần thì vận tốc giảm dần, $\Delta v < 0$
$\Rightarrow a.v<0$
Giải SGK câu hỏi trang 39
$b$) Gia tốc của ô tô trên đoạn đường $4$ có gì đặc biệt so với sự thay đổi vận tốc trên các đoạn đường khác?
$2$. Một con báo đang chạy với vận tốc $30$ $m/s$ thì chuyển động chậm dần khi tới gần một con suối. Trong 3 giây, vận tốc của nó giảm còn $9$ $m/s$. Tính gia tốc của con báo.
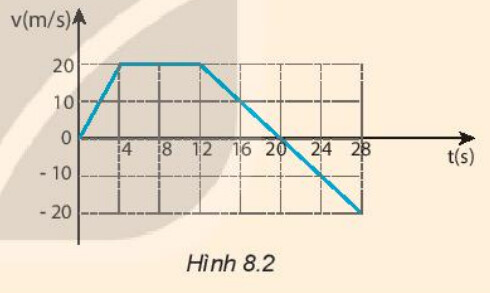
Tính gia tốc của ô tô:
$a$) Trong $4 s$ đầu.
$b$) Từ giây thứ $4$ đến giây thứ $12$.
$c$) Từ giây thứ $12$ đến giây thứ $20$.
$d$) Từ giây thứ $20$ đến giây thứ $28$.
+ Biểu thức tính gia tốc: $a = \frac{\Delta v}{\Delta t}$
+ $1 m/s = 3,6 km/h$
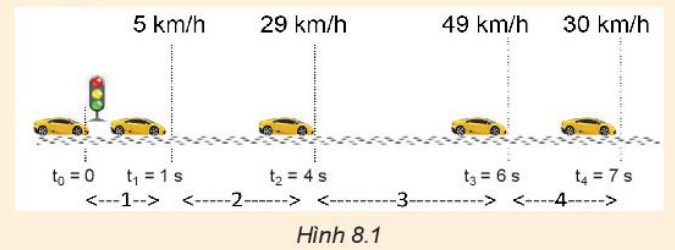
$1$. $a$) Đổi $5 km/h = \frac{145}{18} m/s$; $29 km/h = \frac{245}{18} m/s$; $49 km/h = \frac{245}{18} m/s$; 30 km/h = \frac{ 25}{3} m/s$.
+ Gia tốc trong đoạn đường $1$: $a = \frac{\Delta v}{\Delta t} = \frac{25}{18.1} = \frac{25}{18}\approx 1,39 (m/s^{2})$
+ Gia tốc trong đoạn đường $2$: $ a = \frac{\Delta v}{\Delta t} = \frac{\frac{145}{18}- \frac{25}{18}}{4-1} \approx 2,22(m/s^{2})$
+ Gia tốc trong đoạn đường $3$: $ a = \frac{\Delta v}{\Delta t} = \frac{\frac{245}{18}- \frac{145}{18}}{6-4} \approx 2,78(m/s^{2})$
+ Gia tốc trong đoạn đường $4$: $ a = \frac{\Delta v}{\Delta t} = \frac{\frac{25}{3}- \frac{145}{18}}{7-6} \approx -5,28(m/s^{2})$
$b$) Trong $4$ đoạn đường trên, vận tốc tăng dần, còn gia tốc từ đoạn đường $1$ đến đoạn đường $3$ tăng dần, nhưng từ đoạn đường $3$ đến đoạn đường $4$ thì gia tốc giảm dần.
$2$. Gia tốc của con báo là:
$a = \frac{\Delta v}{\Delta t} = \frac{9-30}{3} = -7 (m/s^{2})$
$3$. $a$) Trong $4 s$ đầu:
$\Delta v = 20 (m/s); \Delta t = 4 (s) \Rightarrow a = \frac{\Delta v}{\Delta t} = \frac{20}{4} = 5 (m/s^{2})$
$b$) Từ giây thứ $4$ đến giây thứ $12$:
$\Delta v = 20 – 20 = 0 (m/s); \Delta t = 12 – 4 = 8 (s) \Rightarrow a = \frac{\Delta v}{\Delta t} = 0 (m/s^{2})$
$c$) Từ giây thứ $12$ đến giây thứ $20$:
$\Delta v = 0 – 20 = -20 (m/s); \Delta t = 20 – 12 = 8 (s) \Rightarrow a = \frac{\Delta v}{\Delta t} = \frac{-20}{8} = -2,5 (m/s^{2})$
$d$) Từ giây thứ $20$ đến giây thứ $28$:
$\Delta v = -20 – 0 = -20 (m/s); \Delta t = 28 – 20 = 8 (s) \Rightarrow a = \frac{\Delta v}{\Delta t} = \frac{-20}{8} = -2,5 (m/s^{2})$
Bài Giải SGK bài 8 chương 2 trang 37, 38, 39 Vật lí 10 Kết nối tri thức của HocThatGioi đã đi đến hồi kết. Hy vọng qua bài học này các bạn sẽ nhận được những điều bổ ích nhé. Hẹn gặp lại các bạn ở những bài học sau nhé. Chúc các bạn học tốt!!!





