Giải SGK bài tập cuối chương 10 trang 102 Toán 7 Kết nối tri thức Tập 2
Sau khi học thật kỹ càng các kiến thức lý thuyết, vận dụng của chương 10 – Một số hình khối trong thực tiễn. Thì bây giờ, các bạn hãy cùng HocThatGioi vận dụng các lý thuyết đó, để hoàn thiện cũng như giải SGK bài tập cuối chương 10 trang 102 Toán 7 Kết nối tri thức Tập 2, một cách nhanh nhất, dễ dàng nhất nhé. Hy vọng các bạn có thể giải nhanh và chính xác các bài tập này, trước khi cần đến sự hỗ trợ của chúng tớ.
Giải SGK bài 10.20 trang 102
a) Tích thể tích của cái hộp.
b) Tính diện tích bìa dùng để làm cái hộp.
$a = 20 cm$, $b = 14 cm$, $h = 15 cm$.
a) $V = a.b.h$.
b) $S_{biadung}=S_{xp} + 2S_{day} = C_{day}.h + 2.a.b = 2(a + b).h + 2ab.$
a) Thể tích của hộp là :
$20.14.15 = 4200 (cm^{3})$
b)
Diện tích bìa để làm hộp bằng diện tích xung quanh + diện tích $2$ mặt đáy của hình hộp chữ nhật.
Diện tích xung quanh của cái hộp là: $2 . (20 + 14) . 15 = 1 020 (cm^{2})$.
Diện tích hai đáy của cái hộp là: $2 . 20 . 14 = 560 (cm^{2})$.
Vậy, diện tích bìa dùng để làm hộp là: $1 020 + 560 = 1 580 (cm^{2})$.
Vậy diện tích bìa để làm hộp là $1580 cm^{2}$.
Giải SGK bài 10.21 trang 102
$S^{xq}=C^{day}.h$
$S^{tp}=S_{xq} + 2S_{day}$
$V=S_{day}.h$
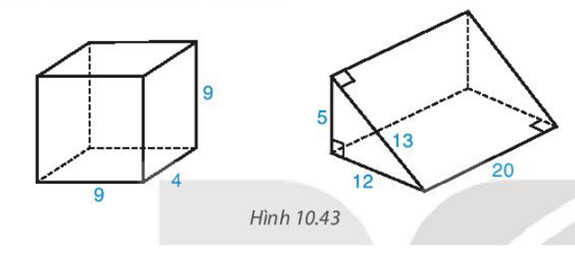
+) Xét hình hộp chữ nhật:
Diện tích xung quanh của hình hộp chữ nhật là: $2 . (9 + 4) . 9 = 234$ (đơn vị diện tích).
Diện tích hai đáy của hình hộp chữ nhật là: $2 . 9 . 4 = 72$ (đơn vị diện tích).
Diện tích toàn phần của hình hộp chữ nhật là: $234 + 72 = 306$ (đơn vị diện tích).
Thể tích của hình hộp chữ nhật là: $9 . 9 . 4 = 324$ (đơn vị thể tích).
+) Xét hình lăng trụ:
Diện tích xung quanh của hình lăng trụ là: $(5 + 12 + 13) . 20 = 600$ (đơn vị diện tích).
Diện tích đáy của hình lăng trụ là: $\frac{1}{2}. 5 . 12 = 30$ (đơn vị diện tích).
Diện tích toàn phần của hình lăng trụ bằng tổng diện tích xung quanh và diện tích hai đáy của hình lăng trụ.
Do đó diện tích toàn phần của hình lăng trụ là: $600 + 2 . 30 = 660$ (đơn vị diện tích).
Thể tích của hình lăng trụ là: $30 . 20 = 600$ (đơn vị thể tích).
Giải SGK bài 10.22 trang 102
a) Tính diện tích xung quanh và diện tích toàn phần của khối hình lập phương.
b) Tìm kích thước mỗi viên gạch.
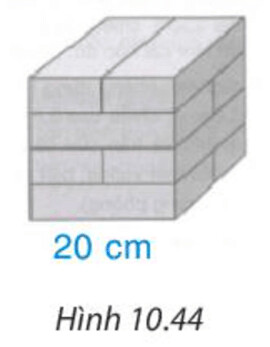
Cạnh $a = 20 cm$
a)$S_{xq} =C_{day}.h = 4a.a = 4a^{2}$
$S_{tp} = S_{xq} + 2S_{day} = 4a^{2}+ 2a^{2} = 6a^{2}$
a) Diện tích xung quanh của khối gạch hình lập phương là: $4.20^{2} = 1 600 (cm^{2})$.
Diện tích toàn phần của khối gạch hình lập phương là: $6.20^{2} = 2400 (cm^{2})$.
b) Trong Hình trên ta thấy chiều dài của viên gạch bằng một cạnh của hình lập phương nên chiều dài của viên gạch là $20$ ($cm$).
Chiều rộng của $2$ viên gạch bằng một cạnh của hình lập phương nên chiều rộng của viên gạch là $20 : 2 = 10$ ($cm$).
Chiều cao của $4$ viên gạch bằng một cạnh của hình lập phương nên chiều cao của viên gạch là $20 : 4 = 5$ ($cm$).
Vậy viên gạch có chiều dài là $20$ $cm$, chiều rộng là $10$ $cm$, chiều cao là $5$ $cm$.
Giải SGK bài 10.23 trang 102
-Tính diện tích xung quanh
-Tính diện tích trần nhà
-Diện tích cần lăn sơn = $(S_{xq} + S_{TranNha}) – S_{cua})$
Diện tích xung quanh của căn phòng là: $2 . (5 + 4) . 3 = 54$ $(m^{2})$.
Diện tích trần nhà là: $5 . 4 = 20$ $(m^{2})$.
Diện tích cần quét sơn bằng tổng diện tích xung quanh và diện tích trần nhà của căn phòng trừ đi diện tích cửa.
Suy ra diện tích cần quét sơn là: $54 + 20 – 5,8 = 68,2$ ($m^{2}$).
Vậy diện tích cần quét sơn là $68,2$ $m^{2}$.
Giải SGK bài 10.24 trang 102
a) Tính diện tích kính dùng để làm bể cá đó
b) Người ta cho vào bể một hòn đá trang trí chìm hẳn trong nước thì mực nước của bể dâng lên thành $37,5$ $cm$. Tính thể tích hòn đá.
a) $S_{kinh} = S_{xq} + S_{day} = 2.(a + b).h + a.b$
b)
-Tính chiều cao tăng thêm của mực nước: $V_{honda} = S_{day}.h_{tangthem}$
a) Diện tích xung quanh của bể cá là: $2 . (80 + 50) . 45 = 11700$ ($cm^{2}$).
Diện tích đáy của bể cá là: $80 . 50 = 4000$ ($cm^{2}$).
Diện tích kính dùng làm bể cá bằng tổng diện tích xung quanh và diện tích một đáy của bể cá.
Do đó diện tích kính dùng để làm bể cá là: $11700 + 4000 = 15700$ ($cm^{2}$).
Vậy diện tích kính dùng để làm bể cá là $15700$ $cm^{2}$.
b) Sau khi cho hòn đá vào thì mực nước tăng lên: $37,5 – 35 = 2,5$ ($cm$).
Thể tích nước dâng lên là: $80 . 50 . 2,5 = 10000$ ($cm^{3}$).
Thể tích hòn đá bằng thể tích nước dâng lên nên thể tích hòn đá bằng $10000$ ($cm^{3}$).
Vậy thể tích của hòn đá bằng $10000$ $cm^{3}$.
Giải SGK bài 10.25 trang 102
-Tính thể tích $1$ viên đá
-Tính tổng thể tích $5$ viên đá
Thể tích của $5$ viên đá là: $5 . 2^{3} = 40$ ($cm^{3}$).
Do cốc chứa đầy nước nên lượng nước trào ra ngoài bằng thể tích của $5$ viên đá.
Vậy thể tích lượng nước trào ra ngoài là $40$ $cm^{3}$.
Vậy là chúng ta đã hoàn thành tất cả các bài tập cuối chương 10 rồi. Các bạn rất thông minh và chăm chỉ. Cảm ơn các bạn đã theo dõi bài Giải SGK bài tập cuối chương 10 trang 102 Toán 7 Kết nối tri thức Tập 2 ngày hôm nay. Hy vọng các bạn có thể nắm rõ các công thức, phương pháp và cách giải nhanh nhất các bài tập ngày hôm nay. Nếu bạn cảm thấy bài viết của HocThatGioi hay và bổ íc thì hãy chia sẽ đến tất cả những người bạn của mình, để cùng nhau học thật giỏi nhé! Chúc các bạn học tốt.





