Giải SGK bài tập cuối chương VII Toán 10 Kết nối tri thức Tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi trắc nghiệm cũng như bài tập tự luận trong bài tập cuối chương VII. Đây là Bài tập cuối chương VII trang 58, 59 sách Toán 10 Kết nối tri thức tập 2. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi trắc nghiệm trong SGK của bài tập cuối chương VII
Sau khi đã học lý thuyết và giải các bài tập ở Chương Phương pháp tọa độ trong mặt phẳng. Cùng HocThatGioi giải chi tiết phần câu hỏi trắc nghiệm ở trang 58 trong bài tập cuối chương VII ngay sau đây nhé!
Bài 7.26 trang 58
A. $2 x-y+1=0$
B. $\left\{\begin{array}{l}x=2 t \\ y=t\end{array}\right.$
C. $x^2+y^2=1$
D. $y=2 x+3$
Phương trình tham số của đường thằng có dạng $\left\{\begin{array}{l}x=x_o+a t \\ y=y_o+b t\end{array} \quad(t \in \mathbb{R})\right.$.
\Rightarrow Chọn B
Bài 7.27 trang 58
A. $-x-2 y+3=0$
B. $\left\{\begin{array}{l}x=2+t \\ y=3-t\end{array}\right.$
C. $y^2=2 x$
D. $\frac{x^2}{10}+\frac{y^2}{6}=1$
Phương trình tổng quát của đường thẳng có dạng $\mathrm{a} x+b y+c=0\left(a^2+b^2 \neq 0\right)$.
\Rightarrow Chọn $\mathrm{A}$
Bài 7.28 trang 58
A. $x^2-y^2=1$
B. $(x-1)^2+(y-2)^2=-4$
C. $x^2+y^2=2$
D. $y^2=8 x$
Phương trình đường tròn có dạng $(x-a)^2+(y-b)^2=c^2$ hoặc $x^2+y^2+2 a x+2 b y+c=0$.
Phương trình $x^2+y^2=2$ là một phương trình đường tròn với $O(0 ; 0)$ là tâm và bán kính $R=\sqrt{2}$.
\Rightarrow Chọn C
Bài 7.29 trang 58
A. $\frac{x^2}{9}+\frac{y^2}{9}=1$
B. $\frac{x^2}{1}+\frac{y^2}{6}=1$
C. $\frac{x^2}{4}-\frac{y^2}{1}=1$
D. $\frac{x^2}{2}+\frac{y^2}{1}=1$
Phương trình chính tắc của elip có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$.
\Rightarrow Chọn D
Bài 7.30 trang 58
A. $\frac{x^2}{3}-\frac{y^2}{2}=-1$
B. $\frac{x^2}{1}-\frac{y^2}{6}=1$
C. $\frac{x^2}{6}+\frac{y^2}{1}=1$
D. $\frac{x^2}{2}+\frac{y^2}{1}=-1$
Phương trình chính tắc của hyperbol có dạng $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$.
\Rightarrow Chọn B.
Bài 7.31 trang 58
A. $x^2=4 y$
B. $x^2=-6 y$
C. $y^2=4 x$
D. $y^2=-4 x$
Phương trình chính tắc của parabol là $y^2=2 p x(p>0)$.
\Rightarrow Chọn C.
Trả lời câu hỏi tự luận trong SGK của bài tập cuối chương VII
Phần tiếp theo sẽ cung cấp cho các bạn phương pháp cùng lời giải trong phần câu hỏi tự luận trang 58, 59 cực kỳ dễ hiểu và chi tiết. Cùng HocThatGioi rèn luyện và nâng cao kỹ năng giải quyết các vấn đề thực tế thông qua các phương pháp, công thức toán học từ Chương Phương pháp tọa độ trong mặt phẳng.
Bài 7.32 trang 58
Sử dụng công thức diện tích $S_{A B C}=\frac{1}{2} d(A, B C).B C$
Ta có: $\overrightarrow{B C}=(-5 ;-1)$.
\Rightarrow $B C=\sqrt{(-5)^2+(-1)^2}=\sqrt{26}$, đồng thời $\overrightarrow{n_{B C}}=(1 ;-5)$.
Mặt khác $\mathrm{BC}$ đi qua điểm $\mathrm{B}(3 ; 5)$ nên phương trình $\mathrm{BC}$ là $x-5 y+22=0$
Độ dài đường cao $\mathrm{AH}$ của tam giác $\mathrm{ABC}$ là:
$A H=d(A, B C)=\frac{|1-5(-1)+22|}{\sqrt{1^2+(-5)^2}}=\frac{28}{\sqrt{26}}$
Diện tích của tam giác $\mathrm{ABC}$ là:
$S_{A B C}=\frac{1}{2} A H . B C=\frac{1}{2}. \frac{28}{\sqrt{26}}. \sqrt{26}=14$
Bài 7.33 trang 58
a) Viết phương trình đường tròn tâm $A$ và đi qua $B$.
b) Viết phương trình tổng quát của đường thẳng $AB$.
c) Viết phương trình đường tròn tâm $O$ và tiếp xúc với đường thẳng $AB$.
a) Đường tròn tâm $\mathrm{A}$ bán kính $\mathrm{AB}$.
b) $\overrightarrow{u_{A B}}=\overrightarrow{A B}=(4 ; 1) \Rightarrow \overrightarrow{n_{A B}}=(1 ;-4)$ và $A B$ đi qua $A(-1 ; 0)$.
c) Đường tròn tâm $O(0 ; 0)$ và bán kính $R=d(O, A B)$.
Phương trình đường tròn tâm $\mathrm{A}$ bán kính $\mathrm{AB}$ là: $(x+1)^2+y^2=17$
b) Ta có $\overrightarrow{u_{A B}}=\overrightarrow{A B}=(4 ; 1) \Rightarrow \overrightarrow{n_{A B}}=(1 ;-4)$.
Phương trình $\mathrm{AB}$ là $1(x+1)-4 y=0 \Leftrightarrow x-4 y+1=0$.
c) Bán kính của đường tròn tâm $\mathrm{O}$, tiếp xúc với đường thẳng $\mathrm{AB}$ là:
$$R=d(O, A B)=\frac{|0-4.0+1|}{\sqrt{1^2+(-4)^2}}=\frac{1}{\sqrt{17}}$$
Phương trình đường tròn tâm $\mathrm{O}$ tiếp xúc $\mathrm{AB}$ là: $x^2+y^2=\frac{1}{17}$
Bài 7.34 trang 58
a) Tìm toạ độ tâm I và bán kính R của (C).
b) Chứng minh rằng điểm $\mathrm{M}(5 ; 1)$ thuộc $(\mathrm{C})$. Viết phương trình tiếp tuyến d của $(\mathrm{C})$ tại $\mathrm{M}$.
a) Sử dụng công thức xác định tâm và bán kính
b) Thay tọa độ điểm $\mathrm{M}$ thỏa mãn phương trình đường tròn. Tiếp tuyến d đi qua điểm $\mathrm{M}$ và có $\overrightarrow{n_d}=\overrightarrow{I M}$.
a) Ta có $I(2 ;-3)$ và $R=\sqrt{2^2+(-3)^2-(-12)}=5$
b) Ta có: $5^2+1^2-4.5+6.1-12=0$ \Rightarrow $\mathrm{M}$ thuộc $(C)$.
Tiếp tuyến $d$ của $(\mathrm{C})$ tại $\mathrm{M}$ có vectơ pháp tuyến là $\overrightarrow{n_d}=\overrightarrow{I M}=(3 ; 4)$, đồng thời $\mathrm{d}$ đi qua điểm $M(5 ; 1)$.
Vậy phương trình của d là $3(x-5)+4(y-1)=0 \Leftrightarrow 3 x+4 y-19=0$.
Bài 7.35 trang 59
a) Tìm các giao điểm $A_{1}, A_{2}$ của $(E)$ với trục hoành và các giao điểm $B_{1}, B_{2}$ của $(E)$ với trục tung. Tính $A_{1} A_{2}, B_{1} B_{2}$.
b) Xét một điểm bất kì $M\left(x_{0}, y_{0}\right)$ thuộc $(E)$.
Chứng minh rằng $b^{2} \leq x_{0}^{2}+y_{0}^{2} \leq a^{2}$ và $b \leq O M \leq a$.
a) Tọa độ $A_1, A_2$ thỏa mãn phương trình $(\mathrm{E})$ và $y=0$. Tọa độ $B_1, B_2$ thỏa mãn phương trình $(\mathrm{E})$ và $x=0$.
b) Sử dụng tính chất $a>b>0$ và đẳng thức $\frac{x_o^2}{a^2}+\frac{y_o^2}{b^2}=1$.
a) Các giao điểm của ( $E$ ) với trục hoành có tọa độ thỏa mãn hệ phương trình
\begin{cases} \frac{\mathrm{ x^2 } }{\mathrm{a^2}} + \frac{\mathrm{ y^2 } }{\mathrm{b^2}}=1 \\ y=0 \\ \end{cases} \Longleftrightarrow \begin{cases} x= \pm a \\ y=0 \\ \end{cases} \Longleftrightarrow \begin{cases} A_1(-a ; 0) \\ A_2(a ; 0) \\ \end{cases}
Các giao điểm của (E) với trục tung có tọa độ thỏa mãn hệ phương trình
\begin{cases} \frac{\mathrm{ x^2 } }{\mathrm{a^2}} + \frac{\mathrm{ y^2 } }{\mathrm{b^2}}=1 \\ y=0 \\ \end{cases} \Longleftrightarrow \begin{cases} x= 0 \\ y= \pm b \\ \end{cases} \Longleftrightarrow \begin{cases} B_1(0 ; -b) \\ B_2(0 ; b) \\ \end{cases}
Ta có $A_1 A_2=2 a, B_1 B_2=2 b$.
b) Do M thuộc (E) nên ta có $\frac{x_o^2}{a^2}+\frac{y_o^2}{b^2}=1$
Do $a>b>0$ nên ta có $\frac{x_0^2}{a^2} \leq \frac{x_o^2}{b^2}$.
Suy ra $1 \leq \frac{x_0^2}{b^2}+\frac{y_o^2}{b^2} \Rightarrow b^2 \leq x_o^2+y_o^2$
Tương tự ta có $\frac{y_o^2}{a^2} \leq \frac{y_o^2}{b^2}$ nên $1 \geq \frac{y_o^2}{a^2} \leq \frac{y_o^2}{b^2} \Rightarrow a^2 \geq x_o^2+y_o^2$
Vậy $b^2 \leq x_o^2+y_o^2 \leq a^2$
Ta có $O M=\sqrt{x_o^2+y_o^2}$ suy ra $b \leq O M \leq a$
Bài 7.36 trang 59
a) Tìm các giao điểm $A_1, A_2$ của hypebol với trục hoành (hoành độ của $A_1$ nhỏ hơn của $A_2$ ).
b) Chứng minh rằng, nếu điểm $\mathrm{M}(x ; y)$ thuộc nhánh nằm bên trái trục tung của hypebol thì $x \leq-a$, nếu điểm $\mathrm{M}(\mathrm{x}, \mathrm{y})$ thuộc nhánh nằm bên phải trục tung của hypebol thì $x \geq a$.
c) Tìm các điểm $M_1, M_2$ tương ứng thuộc các nhánh bên trái, bên phải trục tung của hypebol để $M_1 M_2$ nhỏ nhất.
a) Tọa độ $A_1, A_2$ thỏa mãn phương trình của $(H)$ và $y=0$.
b) Sử dụng $\frac{x^2}{a^2}=1+\frac{y^2}{b^2} \geq 1$
c) $M_1 M_2 \geq\left|x_2-x_1\right| \geq|a-(-a)|=2 a$
a) Các giao điểm của $(H)$ với trục hoành có tọa độ thỏa mãn hệ phương trình:
\begin{cases} \frac{\mathrm{ x^2 } }{\mathrm{a^2}} – \frac{\mathrm{ y^2 } }{\mathrm{b^2}}=1 \\ y=0 \\ \end{cases} \Longleftrightarrow \begin{cases} x= \pm a \\ y= 0 \\ \end{cases} \Longleftrightarrow \begin{cases} A_1(-a ; 0) \\ A_2(a ; 0) \\ \end{cases}
b) Với $M(x ; y)$ thuộc (H) ta có $\frac{x^2}{a^2}=1+\frac{y^2}{b^2} \geq 1 \Rightarrow x^2 \geq a^2 \Rightarrow\left[\begin{array}{l}x \leq-a \\ x \geq a\end{array}\right.$
Do đó nếu $M(x ; y)$ thuộc bên trái trục tung khi thì $x0$, suy ra $x \geq-a$.
c) Gọi $M_1\left(x_1 ; y_1\right), M_2\left(x_2 ; y_2\right)$. vi $M_1$ thuộc nhánh bên trái trục tung nên ta có $x_1 \leq-a, M_2$ thuộc nhánh bên phải trục tung nên ta có $x_2 \geq a$.
Suy ra $M_1 M_2=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \geq \sqrt{\left(x_2-x_1\right)^2}=\left|x_2-x_1\right| \geq|a-(-a)|=2 a$
Dấu “=” xảy ra khi và chỉ khi:
\begin{cases} y_2-y_1=0 \\ x_2=a \\x_1=-a \end{cases} \Longleftrightarrow \begin{cases} x_2=a \\ x_1=-a \\ y_1=y_2=0 \end{cases} \Longleftrightarrow \begin{cases} M_1(-a ; 0) \\ M_2(a ; 0) \\ \end{cases}
Bài 7.37 trang 59
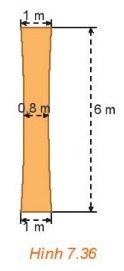
Gắn hệ trục tọa độ với gốc tọa độ trùng với trung điểm của đoạn thẳng ứng với mặt cắt ngang nhỏ nhất của cột trụ.
Khi đó ta có phương trình của $(\mathrm{H})$ là: $\frac{x^2}{0,16}-\frac{y^2}{16}=1$
Độ rộng của trụ ứng với độ cao $5 \mathrm{~m}$ ứng với điểm trên $(\mathrm{H})$ có tung độ bằng 2
Suy ra $\frac{x^2}{0,16}-\frac{2^2}{16}=1 \Rightarrow x \approx 0,45$
Vậy độ rộng của cột trụ tại điểm có chiều cao $5 \mathrm{~m}$ xấp xỉ bằng $2.0,45=0,9(\mathrm{~m})$.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK Bài tập cuối chương Phương pháp tọa độ trong mặt phẳng Toán 10 Kết nối tri thức tập 2 ở các trang 58, 59. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!





