SGK Toán 7 – Kết Nối Tri Thức
Giải SGK Luyện tập chung trang 38 Toán 7 Kết nối tri thức
Các bài tập Luyện tập chung ở trang 38 SGK Toán 7 Kết nối tri thức sẽ giúp các bạn ôn tập lại các kiến thức về Số thập phân vô hạn tuần hần, Số hữu tỉ cũng như là căn bậc 2 số học một cách đầy đủ, chi tiết nhất. Cùng xem HocThatGioi giải quyết các bài toán này nhé!
Giải bài 2.19 trang 38
Cho bốn phân số: $\frac{17}{80} ; \frac{611}{125} ; \frac{133}{91}$ và $\frac{9}{8}$.
a) Phân số nào trong những phân số trên không viết được dưới dạng số thập phân hữu hạn?
b) Cho biết $\sqrt{2}=1,414213562 \ldots$, hãy so sánh phân số tìm được trong câu a) với $\sqrt{2}$.
a) Phân số nào trong những phân số trên không viết được dưới dạng số thập phân hữu hạn?
b) Cho biết $\sqrt{2}=1,414213562 \ldots$, hãy so sánh phân số tìm được trong câu a) với $\sqrt{2}$.
Phương pháp giải:
a)
Cách 1: Viết các phân số dưới dạng số thập phân rồi nhận biết số thập phân hữu hạn.
Cách 2: Sử dụng nhận xét ở phần Em có biết trang 28: Nếu một phân số tối giản có mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn.
b) Viết phân số đó dưới dạng số thập phân rồi so sánh.
a)
Cách 1: Viết các phân số dưới dạng số thập phân rồi nhận biết số thập phân hữu hạn.
Cách 2: Sử dụng nhận xét ở phần Em có biết trang 28: Nếu một phân số tối giản có mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn.
b) Viết phân số đó dưới dạng số thập phân rồi so sánh.
Lời giải chi tiết:
Cách 1:
$\frac{17}{80}=0,2125 ; \frac{611}{125}=4,888 ; \frac{133}{91}=1,(461538) ; \frac{9}{8} =1,125$
Như vậy, trong những phân số trên, phân số không viết được dưới dạng số thập phân hữu hạn là: $\frac{133}{91}$
Cách 2:
Vì các phân số trên đều tối giản và có mẫu dương Ta có: $80=2^4 .5 ; 125=5^3 ; 91=7.13 ; 8=2^3$ nên chí có 91 có ước nguyên tố khác 2,5 nên $\frac{133}{91}$ không viết được dưới dạng số thập phân hữu hạn
b) Ta có: $\frac{133}{91}=1,(461538)=1,461538461538 \ldots$.
Quan sát các chữ số ở các hàng tương ứng từ trái sang phải, vì $1=1 ; 4=4 ; 1<6$ nên $1,414213562 \ldots\sqrt{2}$
Cách 1:
$\frac{17}{80}=0,2125 ; \frac{611}{125}=4,888 ; \frac{133}{91}=1,(461538) ; \frac{9}{8} =1,125$
Như vậy, trong những phân số trên, phân số không viết được dưới dạng số thập phân hữu hạn là: $\frac{133}{91}$
Cách 2:
Vì các phân số trên đều tối giản và có mẫu dương Ta có: $80=2^4 .5 ; 125=5^3 ; 91=7.13 ; 8=2^3$ nên chí có 91 có ước nguyên tố khác 2,5 nên $\frac{133}{91}$ không viết được dưới dạng số thập phân hữu hạn
b) Ta có: $\frac{133}{91}=1,(461538)=1,461538461538 \ldots$.
Quan sát các chữ số ở các hàng tương ứng từ trái sang phải, vì $1=1 ; 4=4 ; 1<6$ nên $1,414213562 \ldots\sqrt{2}$
Giải bài 2.20 trang 38
a) Viết các phân số sau dưới dạng số thập phân vô hạn tuẩn hoàn (dùng dấu ngoặc để chỉ rō chu kì): $\frac{1}{9} ; \frac{1}{99}$.
Em có nhận xét gì vể kết quả nhận được?
b) Em hãy dự đoán dạng thập phân của $\frac{1}{999}$.
Em có nhận xét gì vể kết quả nhận được?
b) Em hãy dự đoán dạng thập phân của $\frac{1}{999}$.
Phương pháp giải:
Bước 1: Thực hiện phép chia.
Bước 2: Quan sát và viết kết quả thành dạng thập phân vô hạn tuần hoàn
Bước 1: Thực hiện phép chia.
Bước 2: Quan sát và viết kết quả thành dạng thập phân vô hạn tuần hoàn
Lời giải chi tiết:
a) – Viết dạng thập phân vô hạn tuần hoàn: $\frac{1}{9} ; \frac{1}{99}$ là: $\frac{1}{9}=0,(1) ; \frac{1}{99}=0,(01)$
– Nhận xét:
Dạng thập phân vô hạn tuần hoàn của phân số có dạng $\frac{1}{99 \ldots 9}$ như sau:
$\frac{1}{99 \ldots 9}=0,(0 \ldots 001)$ ( n chữ số 9); ( $n-1$ chữ số 0 )
b) Dự đoán kết quả của $\frac{1}{999}$
Theo nhận xét ở câu a ta có: $\frac{1}{999}=0,(001)$
a) – Viết dạng thập phân vô hạn tuần hoàn: $\frac{1}{9} ; \frac{1}{99}$ là: $\frac{1}{9}=0,(1) ; \frac{1}{99}=0,(01)$
– Nhận xét:
Dạng thập phân vô hạn tuần hoàn của phân số có dạng $\frac{1}{99 \ldots 9}$ như sau:
$\frac{1}{99 \ldots 9}=0,(0 \ldots 001)$ ( n chữ số 9); ( $n-1$ chữ số 0 )
b) Dự đoán kết quả của $\frac{1}{999}$
Theo nhận xét ở câu a ta có: $\frac{1}{999}=0,(001)$
Giải bài 2.21 trang 38
Viết $\frac{5}{9}$ và $\frac{5}{99}$ dưới dạng số thập phân vô hạn tuẳn hoàn.
Phương pháp giải:
Bước 1: Thực hiện phép chia $5:9$ và $5:99$ để thu được kết quả là số thập phân
Bước 2: Nhận ra chu kì của mỗi số thập phân
Bước 1: Thực hiện phép chia $5:9$ và $5:99$ để thu được kết quả là số thập phân
Bước 2: Nhận ra chu kì của mỗi số thập phân
Lời giải chi tiết:
Ta có:
$\frac{5}{9}=0,5555 \ldots=0,(5) $
$\frac{5}{99}=0,050505 \ldots=0,(05)$
Ta có:
$\frac{5}{9}=0,5555 \ldots=0,(5) $
$\frac{5}{99}=0,050505 \ldots=0,(05)$
Giải bài 2.22 trang 38
Nam vẽ một phẳn trục số trên vở ô li và đánh dấu ba điểm $A, B, C$ như sau:
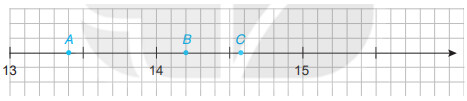
a) Hãy cho biết hai điểm $A, B$ biểu diễn nhūng số thập phân nào?
b) Làm tròn số thập phân được biểu diễn bởi điểm $C$ với độ chính xác 0,05 .

a) Hãy cho biết hai điểm $A, B$ biểu diễn nhūng số thập phân nào?
b) Làm tròn số thập phân được biểu diễn bởi điểm $C$ với độ chính xác 0,05 .
Phương pháp giải:
a) Đếm số vạch chia trên một đơn vị
Tìm khoảng cách từ mỗi điểm đến điểm mốc $13,14$
b) Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác $0,05$ tức là làm tròn đến chữ số thập phân thứ nhất.
a) Đếm số vạch chia trên một đơn vị
Tìm khoảng cách từ mỗi điểm đến điểm mốc $13,14$
b) Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác $0,05$ tức là làm tròn đến chữ số thập phân thứ nhất.
Lời giải chi tiết:
Mỗi đơn vị được chia thành 10 phần bằng nhau nên khoảng cách giữa 2 vạch chia liên tiếp là 0,1 đơn vị.
a) Điểm A biểu diễn số $13,4$
Điểm B biểu diễn số $14,2$
b) Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác $0,05$, ta được $14,6$ (vì điểm C nằm gần vạch biểu thị số 14,6 nhất).
Mỗi đơn vị được chia thành 10 phần bằng nhau nên khoảng cách giữa 2 vạch chia liên tiếp là 0,1 đơn vị.
a) Điểm A biểu diễn số $13,4$
Điểm B biểu diễn số $14,2$
b) Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác $0,05$, ta được $14,6$ (vì điểm C nằm gần vạch biểu thị số 14,6 nhất).
Giải bài 2.23 trang 38
Thay dấu “?” bằng chứ số thích hợp.
a) $-7,02<-7, ?(1)$
b) $-15,3 ? 021<-15,3819$
a) $-7,02<-7, ?(1)$
b) $-15,3 ? 021<-15,3819$
Phương pháp giải:
So sánh các chữ số ở vị trí tương ứng của hai số thập phân
Chú ý: Để so sánh 2 số thập phân âm, ta so sánh 2 số thập phân đối của chúng.
So sánh các chữ số ở vị trí tương ứng của hai số thập phân
Chú ý: Để so sánh 2 số thập phân âm, ta so sánh 2 số thập phân đối của chúng.
Lời giải chi tiết:
a) $ -6,02 < -7,0(1)$
b) $-15.39021 < -15,2819$
a) $ -6,02 < -7,0(1)$
b) $-15.39021 < -15,2819$
Giải bài 2.24 trang 38
So sánh:
a) $12,26$ và $12,(24)$;
b) $31,3(5)$ và $29,9(8)$.
a) $12,26$ và $12,(24)$;
b) $31,3(5)$ và $29,9(8)$.
Phương pháp giải:
So sánh các chữ số ở vị trí tương ứng của hai số thập phân
So sánh các chữ số ở vị trí tương ứng của hai số thập phân
Lời giải chi tiết:
a) Ta có: $12,(24) = 12,242424….$
Đi từ trái sang phải, chữ số thập phân thứ 2 của 2 số khác nhau. Vì $ 6 > 4 $ nên $12,26 >12,(24)$
b)
Đi từ trái sang phải, chữ số ở hàng chục của 2 số khác nhau. $3 > 2$ nên $31,3(5) > 29,9(8)$
a) Ta có: $12,(24) = 12,242424….$
Đi từ trái sang phải, chữ số thập phân thứ 2 của 2 số khác nhau. Vì $ 6 > 4 $ nên $12,26 >12,(24)$
b)
Đi từ trái sang phải, chữ số ở hàng chục của 2 số khác nhau. $3 > 2$ nên $31,3(5) > 29,9(8)$
Giải bài 2.25 trang 38
Tính: a) $\sqrt{1}$;
b) $\sqrt{1+2+1}$;
c) $\sqrt{1+2+3+2+1}$.
b) $\sqrt{1+2+1}$;
c) $\sqrt{1+2+3+2+1}$.
Phương pháp giải:
Tính biểu thức dưới dấu căn rồi tìm căn bậc hai số học của số đó
Tính biểu thức dưới dấu căn rồi tìm căn bậc hai số học của số đó
Lời giải chi tiết:
a) $\sqrt{1}=1$
b) $\sqrt{1+2+1}=\sqrt{4}=2$
c) $\sqrt{1+2+3+2+1}=\sqrt{9}=3$
a) $\sqrt{1}=1$
b) $\sqrt{1+2+1}=\sqrt{4}=2$
c) $\sqrt{1+2+3+2+1}=\sqrt{9}=3$
Giải bài 2.26 trang 38
Tinh:
a) $(\sqrt{3})^{2}$;
b) $(\sqrt{21})^{2}$.
a) $(\sqrt{3})^{2}$;
b) $(\sqrt{21})^{2}$.
Phương pháp giải:
$(\sqrt{a})^2=a$
$(\sqrt{a})^2=a$
Lời giải chi tiết:
a) $(\sqrt{3})^2=3$
b) $(\sqrt{21})^2=21$
a) $(\sqrt{3})^2=3$
b) $(\sqrt{21})^2=21$





