Lý thuyết bất đẳng thức Cosi (Cauchy) toán lớp 10 cực chi tiết
Trong bài viết này, hãy cũng HocThatGioi đi tìm hiểu tất tần tật những kiến thức về bất đẳng thức Cosi trong chương trình toán 10. Bài viết này sẽ giúp bạn nắm được cơ bản về bất đẳng thức Cosi cũng như cách để giải những bài toán về chủ đề này. Cùng đi vào bài học ngay nhé!
1. Bất đẳng thức Cosi là gì
Bất đẳng thức Côsi là một trong những bất đẳng thức cổ điển. Tên chính xác là bất đẳng thức giữa trung bình cộng và trung bình nhân, nhiều người gọi là bất đẳng thức AM – GM (AM là viết tắt của Arithmetic mean và GM là viết tắt của Geometric mean). Do nhà toán học người Pháp Augustin – Louis Cauchy (1789 – 1857), người đã đưa ra một cách chừng mình đặc sắc nên nhiều người hay gọi là bất đẳng thức Cauchy.
2. Biểu diễn bất đẳng thức Cosi
Cho x1, x2, x3 ,…, xn là các số thực không âm:
Có nhiều cách để biểu diễn bất đẳng thức Cosi, nhưng thường rơi vào những dạng sau:
- Dạng 1: x_1+x_2+x_3+...+x_n \geqslant n.\sqrt[n]{x_1x_2x_3...x_n}
- Dạng 2: \frac{x_1+x_2+x_3+...+x_n}{n} \geqslant \sqrt[n]{x_1x_2x_3...x_n}
- Dạng 3: {(\frac{x_1+x_2+x_3+...+x_n}{n})}^n \geqslant x_1x_2x_3...x_n
Dấu đẳng thức (=) xảy ra khi x_1=x_2=x_3=...=x_n
Cho x1, x2, x3 ,…, xn là các số thực dương, ta có:
- Dạng 1: \frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}+...+\frac{1}{x_n}\geqslant \frac{n^2}{x_1+x_2+...x_n}
- Dạng 2: (x_1+x_2+...x_n).(\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}+...+\frac{1}{x_n}) \geqslant n^2
Dấu đẳng thức (=) xảy ra khi x_1=x_2=x_3=...=x_n
Tuy nhiên các bạn chỉ cần lựa chọn và nhớ cho mình 1 trong các dạng trên là quá đủ vì từ 1 dạng vẫn có thể suy ra các dạng còn lại. HocThatGioi khuyên bạn chỉ nên nhớ dạng đầu tiên vì nó khá dễ nhớ và dễ dùng.
Ví dụ: Cho 2 số thực a,b không âm, từ bất đẳng thức Cosi, ta có thể suy ra được: a+b \geqslant 2\sqrt{ab}
3. Các bất đẳng thức Cosi đặc biệt
Dưới đây là những bất đẳng thức Cosi đặc biệt mà bạn có thể nhớ để áp dụng vào giải bài tập nhanh hơn.

4. Một số bất đẳng thức được suy ra từ bất đẳng thức Cosi
Dưới đây là một số bất đẳng thức được suy ra từ bất đẳng thức Cosi:
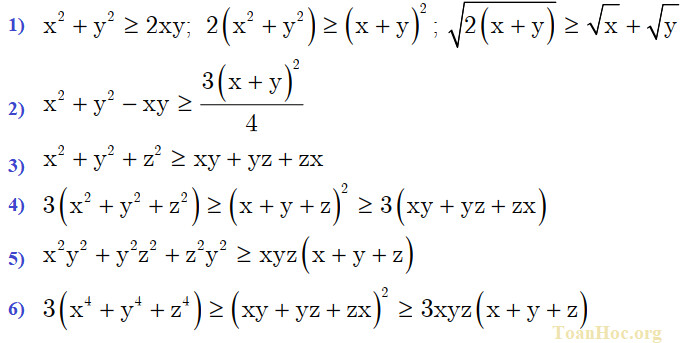
5. Lưu ý khi sử dụng bất đẳng thức Cosi
Khi sử dụng bất đẳng thức Cosi, các bạn cần phải đặc biệt chú ý những lưu ý sau:
- Khi áp dụng bất đẳng thức cô si thì các số phải là những số không âm
- Bất đẳng thức côsi thường được áp dụng khi trong BĐT cần chứng minh có tổng và tích
- Điều kiện xảy ra dấu ‘=’ là các số bằng nhau
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Bất đẳng thức Cosi. Hi vọng các bạn đã có thêm cho mình được những kiến thức bổ ích qua bài viết trên. Nếu thấy bài viết này hay, ý nghĩa hãy chia sẽ nó đến với bạn bè của mình để cùng nhau học thật giỏi nhé! Chúc các bạn học tốt!





