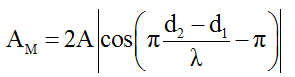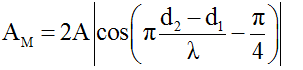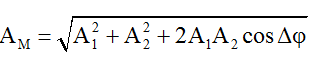Lý thuyết giao thoa sóng hay chi tiết nhất – 8 dạng bài thường gặp

Ở bài trước, ta đã tìm hiểu về bài sóng cơ và sự truyền sóng cơ. Hôm nay, ta sẽ tiếp tục một bài về sóng cơ nữa, đó là giao thoa sóng. Vậy giao thoa sóng là gì? Có các công thức vật lý như thế nào? Làm sao để giải các bài toán về giao thoa sóng? Bài viết này sẽ giúp các bạn trả lời được tất tần tật các nội dung đó. Thế thì còn đợi gì nữa, mau cùng HocThatGioi bắt đầu bài học ngay nào!

1. Lý thuyết giao thoa sóng

1.1 Hiện tượng giao thoa sóng

Quan sát hiện tượng giao thoa sóng trên mặt nước, ta quan sát thấy:

• Trong vùng gặp nhau (vùng giao thoa của hai sóng) xuất hiện những điểm mà tại đó nước dao động mạnh và những điểm mà tại đó nước yên lặng (đứng yên không dao động).
• Hiện đó gọi là hiện tượng giao thoa sóng. Các gợn sóng có hình các đường hypebol gọi là các vân giao thoa.

1.2 Định nghĩa giao thoa sóng

Giao thoa sóng là sự tổng hợp của hai sóng kết hợp trong không gian, trong đó có những chỗ biên độ sóng được tăng cường hay bị giảm bớt.

Điều kiện để có giao thoa: Do hai nguồn kết hợp tạo ra. Hai nguồn kết hợp là hai nguồn có cùng tần số và có hiệu số pha không đổi theo thời gian.

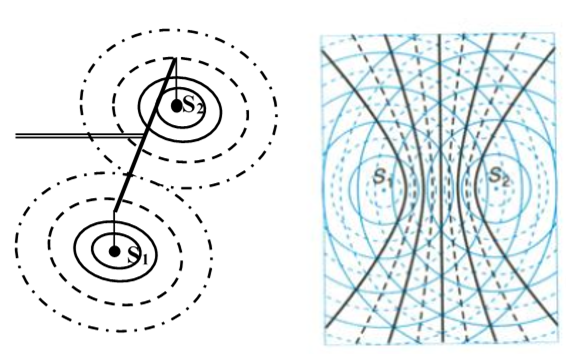
2. Khảo sát sự giao thoa của hai sóng phát ra từ hai nguồn sóng kết hợp S₁, S₂ cùng biên độ A

Xét điểm M cách hai nguồn lần lượt d_1, d_2;

2.1 Phương trình sóng tại 2 nguồn:

u_1= Acos(2πft + Φ_1) và u_2 = Acos(2πft + Φ_2)

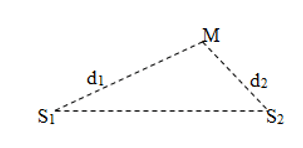
Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:

• u_{1M}=Acos(2 \pi ft +\varphi_1-2 \pi \frac{d_1}{\lambda});
• u_{2M}=Acos(2 \pi ft +\varphi_2 - 2 \pi \frac{d_2}{\lambda});

2.2 Phương trình giao thoa sóng tại M:

u_M=u_{1M} +u_{2M};

=2Acos[ \frac{d_2-d_1}{ \lambda}-\frac{\Delta \varphi}{2}] cos[ 2 \pi f t- \pi \frac{d_1+d_2}{\lambda}+\frac{ \varphi _1+\varphi_2}{x}];

2.3 Biên độ dao động tại M

A_M=2A|cos(\pi \frac{d_2-d_1}{\lambda}-\frac{\Delta \varphi}{2})|;

với \Delta \varphi = \varphi_2- \varphi_1

Những điểm có biên độ cực đại: AM = 2A

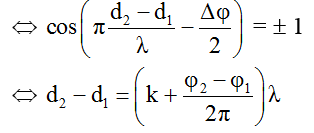
(2 sóng từ 2 nguồn cùng pha nhau tại M)

Những điểm có biên độ cực tiểu:

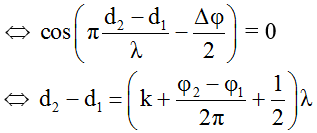
(2 sóng từ 2 nguồn ngược pha nhau tại M)

(k = 0, ± 1, ± 2,… là thứ tự các tập hợp điểm đứng yên kể từ M_0 , k = 0 là tập hợp điểm đứng yên thứ 1)

2.4 Hai nguồn dao động cùng pha 

(∆φ = φ_2 – φ_1 = 0 hoặc = 2kπ).

Thay φ_1 = φ_2= φ vào các phương trình trên ta được:

Phương trình giao thoa sóng tại M:

u_M=u_{1M}+u_{2M}=2A cos(\pi \frac{d_2-d_1}{\lambda})cos(2 \pi f t - \pi \frac{d_1+d_2}{\lambda} +\varphi);

Biên độ sóng tổng hợp:

A_{Mmax}= 2A khi: Hai sóng thành phần tại M cùng pha nhau ∆ φ_{M_1/M_2} = 2kπ (k∈Z).

Khi đó hiệu đường đi: ∆d = d_2 – d_1 = kλ

AM min = 0 khi:

• Hai sóng thành phần tại M ngược pha nhau ∆ φ_{M_1/M_2}= (2k + 1)π (k ∈ Z).
• Hiệu đường đi: ∆d = d_2 – d _1= (k + 1/2 )λ.

Tìm số điểm dao động cực đại trên đoạn S_1S_2: d_1 – d_2 = kλ(k ∈ Z) ;

Số điểm cực đại: \frac{-S_1S_2}{λ} ≤ k ≤\frac{ S_1S_2}{λ}

Tìm số điểm dao động cực tiểu trên đoạn S_1S_2: d_1 – d_2 = (2k + 1)λ/2 (k ∈ Z)

Số điểm cực tiểu: \frac{-S_1S_2}{λ}-\frac{1}{2} ≤ k ≤ \frac{ S_1S_2}{λ}-\frac{1}{2}

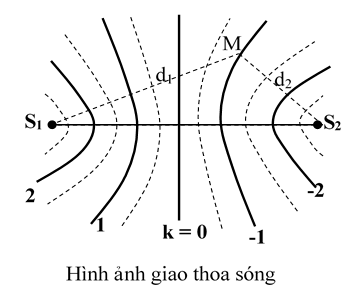
Khi hai nguồn dao động cùng pha và cùng biên độ A thì trung điểm của S_1S_2  có biên độ cực đại A_{max} = 2A và tập hợp các điểm cực tiểu và cực đại là họ các đường Hypecbol có S_1, S_2 là tiêu điểm.

2.5 Hai nguồn dao động ngược pha

 (∆φ = φ_2 – φ_1 = π)

Phương trình giao thoa sóng tại M:

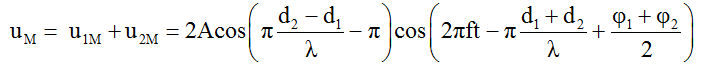
Biên độ sóng tổng hợp:

 

Điểm dao động cực đại: d_2 – d_1 = (k + 1/2)λ (k∈Z)

Số đường hoặc số điểm dao động cực đại (không tính hai nguồn) trên đoạn S_1S_2:

-S_1S_2/λ - 1/2 ≤ k ≤ S_1S_2/λ - 1/2

Điểm dao động cực tiểu (không dao động):

d_2 – d_1 = kl (k∈Z)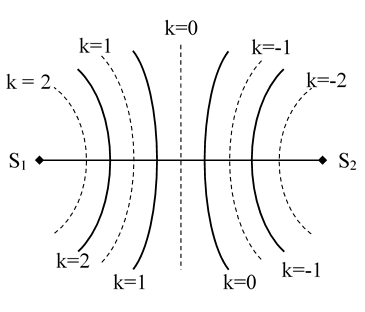

Số đường hoặc số điểm dao động cực tiểu (không tính hai nguồn) trên đoạn S_1S_2:

-S_1S_2/λ ≤ k ≤ S_1S_2/λ

Vậy khi hai nguồn dao động cùng biên độ A và ngược pha thì trung điểm của S_1S_2 có biên độ cực tiểu A{min}=0.

2.6 Trường hợp hai nguồn dao động vuông pha nhau

(∆φ = φ_2 – φ_1 = π/2)

Phương trình giao thoa sóng tại M:

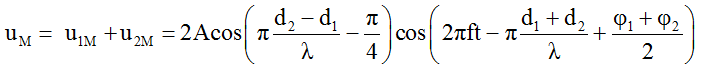
Biên độ sóng tổng hợp:

 

Điểm dao động cực đại: d_2 – d_1= (k + 1/4)λ (k∈Z)

Số đường hoặc số điểm dao động cực đại trên đoạn S_1S_2 :

-S_1S_2/λ-1/4 ≤ k ≤ S_1S_2/λ-1/4

Điểm dao động cực tiểu (không dao động): d_2– d_1 = (k + 3/4)λ (k∈Z)

Số đường hoặc số điểm dao động cực tiểu trên đoạn S_1S_2:

-S_1S_2/λ-3/4 ≤ k ≤ S_1S_2/λ-3/4

Vậy khi hai nguồn dao động cùng biên độ A và vuông pha thì trung điểm của S_1S_2 có biên độ bằng A_M = A \sqrt{2} .

2.7 Trường hợp tổng quát

Hai nguồn cùng tần số, khác biên độ, khác pha ban đầu.

Phương trình sóng tại 2 nguồn:

u_1 = A_1cos(2πft + φ_1) và u_2 = A_2cos(2πft + φ_2)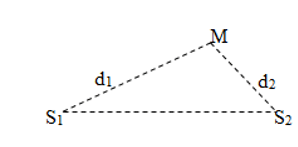

Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:

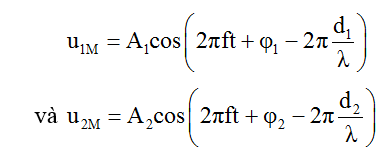
Phương trình giao thoa sóng tại M:

Sử dụng phương pháp tổng hợp hai dao động điều hòa bằng vectơ quay, ta xác định được:

u_M = u{1M} + u{2M} = A_M cos (2πft + φ_M)

Trong đó: 

∆φ là độ lệch pha của hai dao động sóng tới tại M: ∆φ = φ_2 - φ_1 = 2π. (d_2-d_1)/λ

→ │A_1 – A_2│ ≤ AM ≤ A_1 + A_2

+ Điểm M dao động với biên độ cực đại AM = A_1+ A_2 khi và chỉ khi dao động sóng từ hai nguồn tới M đồng pha với nhau: ∆φ = 2kπ

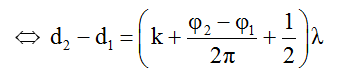
+ Điểm M dao động với biên độ cực tiểu AM = │A_1 – A_2│ khi và chỉ khi dao động sóng từ hai nguồn tới M ngược pha với nhau: ∆φ = (2k + 1)π

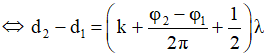
+ Tổng quát: Điểm M dao động với biên độ bất kỳ AM khi và chỉ khi dao động sóng từ hai nguồn tới M lệch pha với nhau: ∆φ = ± α + 2kπ với α thỏa mãn

3. Nhiễu xạ sóng

3.1 Định nghĩa nhiễu xạ sóng

Nhiễu xạ là hiện tượng sóng bị bẻ cong khỏi phương truyền thẳng khi đi qua gần mép vật cản.

3.2 Đặc điểm nhiễu xạ sóng

• Nhiễu xạ xảy ra trên mọi loại sóng, cùng với giao thoa trở thành đặc trưng nhận diện tính chất sóng của các hiện tượng vật lý nhất định nào đó.
• Khác với phản xạ và khúc xạ, vốn xảy ra trên mặt phân cách giữa hai môi trường, nhiễu xạ tự nó xảy ra trong cùng một môi trường đồng nhất. Trái ngược với “nhiễu xạ” là “truyền thẳng”.

3.3 Quan sát nhiễu xạ sóng

Nhiễu xạ chỉ trở nên dễ quan sát khi kích thước vật cản không vượt quá bước sóng vài chục hoặc vài trăm lần. Vật cản ở đây có thể là khe, lỗ, tường, cột.. Nếu vật cản có kích thước quá lớn, lớn hơn bước sóng tầm nghìn lần trở lên, hiệu ứng nhiễu xạ sẽ trở nên khó quan sát và chúng ta thấy gần như chúng truyền thẳng.

Ví dụ:

Sóng nước là trường hợp dễ quan sát hiện tượng nhiễu xạ nhất.:

4. Các dạng bài thường gặp

• Dạng 1: Viết phương trình giao thoa sóng, Tìm biên độ sóng tại 1 điểm
• Dạng 2: Cách xác định số điểm dao động với biên độ cực đại, cực tiểu
• Dạng 3: Bài toán giao thoa tại M có tính chất đặc biệt
• Dạng 4: Xác định biên độ, li độ, vận tốc, gia tốc trong miền giao thoa sóng
• Dạng 5: Tìm số điểm dao động cực đại, cực tiểu giữa hai nguồn, hai điểm bất kì trong giao thoa sóng
• Dạng 6: Bài toán về điểm cực đại, cực tiểu gần nhất, xa nhất với nguồn trong giao thoa sóng
• Dạng 7: Xác định vị trí, số điểm dao động cùng pha, ngược pha với nguồn trong giao thoa sóng
• Dạng 8: Xác định vị trí của điểm cực đại cùng pha, ngược pha với nguồn trong giao thoa sóng

Bài viết khác liên quan đến Lớp 12 – Vật Lý – Giao thoa sóng

• 2 dạng bài tập về giao thoa sóng cơ hay gặp và có đáp án chi tiết