Vật lí 11
Cách giải bài tập liên quan đến sự điều tiết của mắt cực chi tiết
Bài viết sau đây, HocThatGioi sẽ trình bày cho các bạn về Dạng bài tập liên quan đến sự điều tiết của Mắt kèm đáp án lời giải chi tiết để các bạn tham khảo nhé! Nếu các bạn chưa xem phần lý thuyết thì có thể xem lại tại bài Lý thuyết về Mắt và các dụng cụ quang học nhé!
1. Bài toán liên quan đến sự điều tiết của mắt
Đối với dạng toán này thì có một số lý thuyết và công thức mà các bạn cần nắm.
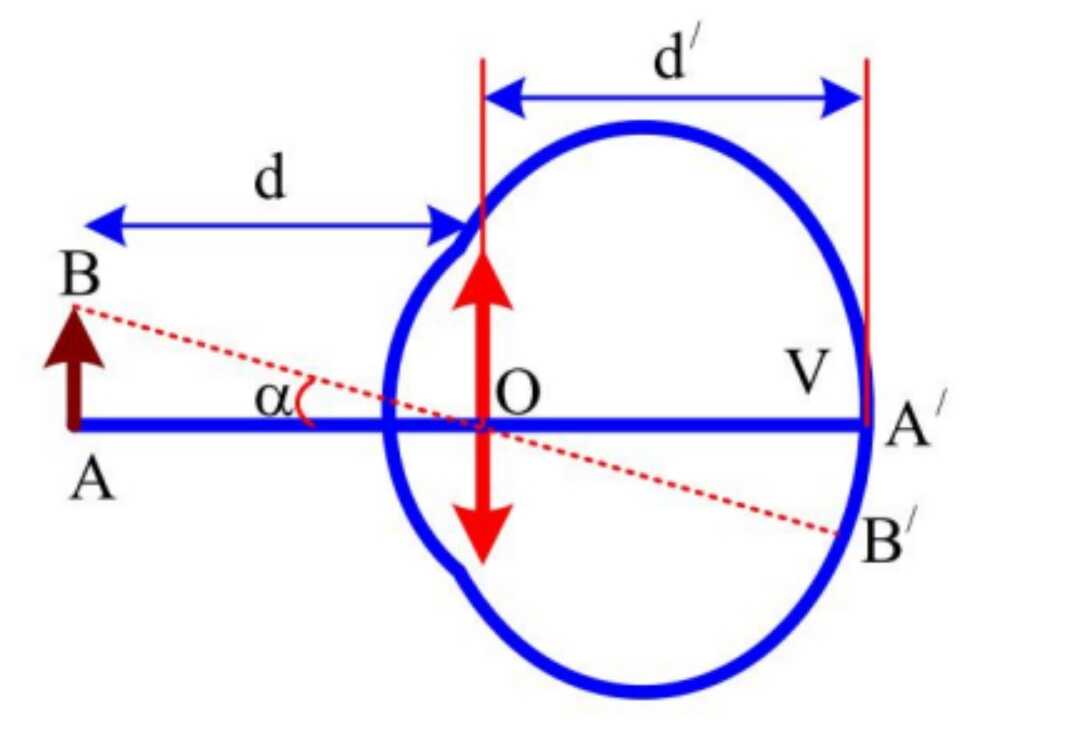
- Khi quan sát trong trạng thái bất kì:
Độ tụ của mắt khi quan sát ở trạng thái bất kì:
D=\frac{1}{f}=\frac{1}{d} +\frac{1}{OV}
- Khi quan sát trong trạng thái không điều tiết D_{min} (vật đặt tại điểm cực viễn: d=OC_{V} (mắt không có tật OC_{V}=\infty).
- Khi quan sát trong trạng thái điều tiết tối đa D_{max} (vật đặt tại điểm cực cận): d=OC_V.
- Độ biến thiên độ tụ của mắt:
Độ biến thiên độ tụ của mắt:
\Delta D= D_{max}- D_{min}
- Góc trông vật trực tiếp:
Góc trông vật trực tiếp:
tan\alpha =\frac{AB}{d}
- Khoảng cách giữa hai đầu dây thần kinh thị giác liên tiếp là:
Khoảng cách giữa hai đầu dây thần kinh thị giác liên tiếp:
A’B’=OV.tan\varepsilon
2. Ví dụ minh họa về bài toán liên quan đến sự điều tiết của mắt
Dưới đây, là một vài ví dụ liên quan đến bài toán về sự điều tiết của mắt có kèm lời giải để các bạn tham khảo nhé!
Câu 1: Một người có thể nhìn rõ các vật cách mắt từ 10 cm đến 100 cm. Độ biến thiên độ tụ cả mắt người từ trạng thái không điều tiết đến trạng thái điều tiết tối đa là ?
Hướng dẫn giải:
Khi quan sát trong trạng thái không điều tiết thì độ tụ sẽ được tính theo công thức:
D_{min}=\frac{1}{f_{max}}=\frac{1}{OC_V}+\frac{1}{OV}
Khi quan sát trong trạng thái điều tiết tối đa thì có độ tụ:
D_{max}=\frac{1}{f_{min}}=\frac{1}{OC_C}+\frac{1}{OV}
Độ biến thiên độ tụ của mắt:
\Delta D= D_{max}- D_{min}=\frac{1}{OC_C}-\frac{1}{OC_V}=\frac{1}{0,1}-\frac{1}{1}(dp)
Khi quan sát trong trạng thái không điều tiết thì độ tụ sẽ được tính theo công thức:
D_{min}=\frac{1}{f_{max}}=\frac{1}{OC_V}+\frac{1}{OV}
Khi quan sát trong trạng thái điều tiết tối đa thì có độ tụ:
D_{max}=\frac{1}{f_{min}}=\frac{1}{OC_C}+\frac{1}{OV}
Độ biến thiên độ tụ của mắt:
\Delta D= D_{max}- D_{min}=\frac{1}{OC_C}-\frac{1}{OC_V}=\frac{1}{0,1}-\frac{1}{1}(dp)
Câu 2: Một người có thể nhìn rõ các vật cách mắt 12 cm thì mắt không phải điều tiết. Lúc đó, độ tụ của thủy tinh thể là 62,5 (dp). Khoảng cách từ quang tâm thủy tinh thể đến võng mạc là bao nhiêu ?
Hướng dẫn giải:
Khi quan sát trong trạng thái không điều tiết thì độ tụ được tính theo công thức sau:
D_{min}=\frac{1}{f_{max}}=\frac{1}{OC_V}+\frac{1}{OV}
\Leftrightarrow 6,25=\frac{1}{0,12}+ \frac{1}{OV}
\rightarrow OV= 0,018 (m)
Khi quan sát trong trạng thái không điều tiết thì độ tụ được tính theo công thức sau:
D_{min}=\frac{1}{f_{max}}=\frac{1}{OC_V}+\frac{1}{OV}
\Leftrightarrow 6,25=\frac{1}{0,12}+ \frac{1}{OV}
\rightarrow OV= 0,018 (m)
Câu 3: Một người mắt bình thường không có tật, quang tâm nằm cách võng mạc một khoảng 2,2 cm. Độ tụ của mắt đó khi quan sát một vật cách mắt 20 cm bằng bao nhiêu ?
Hướng dẫn giải:
Khi quan sát một vật cách mắt thì độ tụ được tính bởi công thức sau:
D=\frac{1}{d}+\frac{1}{OV}=\frac{1}{0,2}+\frac{1}{2,2.10^{-2}}=54,45 (dp)
Khi quan sát một vật cách mắt thì độ tụ được tính bởi công thức sau:
D=\frac{1}{d}+\frac{1}{OV}=\frac{1}{0,2}+\frac{1}{2,2.10^{-2}}=54,45 (dp)
Câu 4: Mắt của một người có quang tâm cách võng mạc khoảng 1,52 cm. Tiêu cư thể thủy tinh thay đổi giữa hai giá trị f_1=1,5 cm và f_2=1,415 cm. Khoảng nhìn rõ của mắt nhất bằng bao nhiêu ?
Hướng dẫn giải:
Khi mắt quan sát trong trạng thái không điều tiết:
D_{min}=\frac{1}{f_{max}}=\frac{1}{OC_V}+\frac{1}{OV}
\rightarrow \frac{1}{1,5}=\frac{1}{OC_V}+\frac{1}{1,52} (1)
Khi mắt quan sát trong trạng thái điều tiết tối đa:
D_{max}=\frac{1}{f_{min}}=\frac{1}{OC_C}+\frac{1}{OV}
\rightarrow \frac{1}{1,415}=\frac{1}{OC_C}+\frac{1}{1,52} (2)
Từ (1) và (2) ta có:
OC_V=114
OC_C= 20,48
Khoảng cách nhìn rõ của mắt là:
O_CO_V= OC_V- OC_C= 114-20,48=93,52 (cm)
Khi mắt quan sát trong trạng thái không điều tiết:
D_{min}=\frac{1}{f_{max}}=\frac{1}{OC_V}+\frac{1}{OV}
\rightarrow \frac{1}{1,5}=\frac{1}{OC_V}+\frac{1}{1,52} (1)
Khi mắt quan sát trong trạng thái điều tiết tối đa:
D_{max}=\frac{1}{f_{min}}=\frac{1}{OC_C}+\frac{1}{OV}
\rightarrow \frac{1}{1,415}=\frac{1}{OC_C}+\frac{1}{1,52} (2)
Từ (1) và (2) ta có:
OC_V=114
OC_C= 20,48
Khoảng cách nhìn rõ của mắt là:
O_CO_V= OC_V- OC_C= 114-20,48=93,52 (cm)
Câu 5: Một người có thể nhìn thấy rõ các vật cách mắt 12 cm thì mắt không phải điều tiết. Lúc đó, độ tụ của thủy tinh thể là 62,5 (dp). Khi quan sát trong trạng thái điều tiết tối đa thì độ tụ của thủy tinh thể là 67,5 (dp). Khoảng cách từ điểm cực cận đến điểm cực mắt bằng bao nhiêu ?
Hướng dẫn giải:
Áp dụng công thức dộ biến thiên của độ tụ ta có:
D_{max}- D_{min}=\frac{1}{OC_C}-\frac{1}{OC_V}
\Leftrightarrow 67,5- 62,5= \frac{1}{OC_C}-\frac{1}{12}
\rightarrow OC_C= 7,5 (cm)
Áp dụng công thức dộ biến thiên của độ tụ ta có:
D_{max}- D_{min}=\frac{1}{OC_C}-\frac{1}{OC_V}
\Leftrightarrow 67,5- 62,5= \frac{1}{OC_C}-\frac{1}{12}
\rightarrow OC_C= 7,5 (cm)
Như vậy, bài viết về Dạng toán sự điều tiết về mắt đến đây đã hết. Qua bài viết này, hi vọng sẽ giúp các bạn tiếp thu được các kiến thức bổ ích. Đừng quên Like và Share để HocThatGioi ngày càng phát triển. Cảm ơn tất cả các bạn đã theo dõi hết bài viết và chúc các bạn học tốt nhé!





