Cách giải và bài tập cực hay về số bội giác và góc trông có lời giải chi tiết
Bài viết sau đây, HocThatGioi xin được tổng hợp Cách giải bài tập liên quan đến số bội giác và góc trông cực hay kèm lời giải chi tiết để các bạn cùng tham khảo nhé! Hãy theo dõi hết bài viết để học hiệu quả hơn và các bạn có thể xem thêm bài lý thuyết về mắt tại bài Lý thuyết Mắt- các dụng cụ quang học nữa nhé!
1. Cách giải bài tập liên quan đến số bội giác và góc trông
Dưới đây, sẽ là một số công thức liên quan đến góc trông, số bội giác mà các bạn cần nhớ.
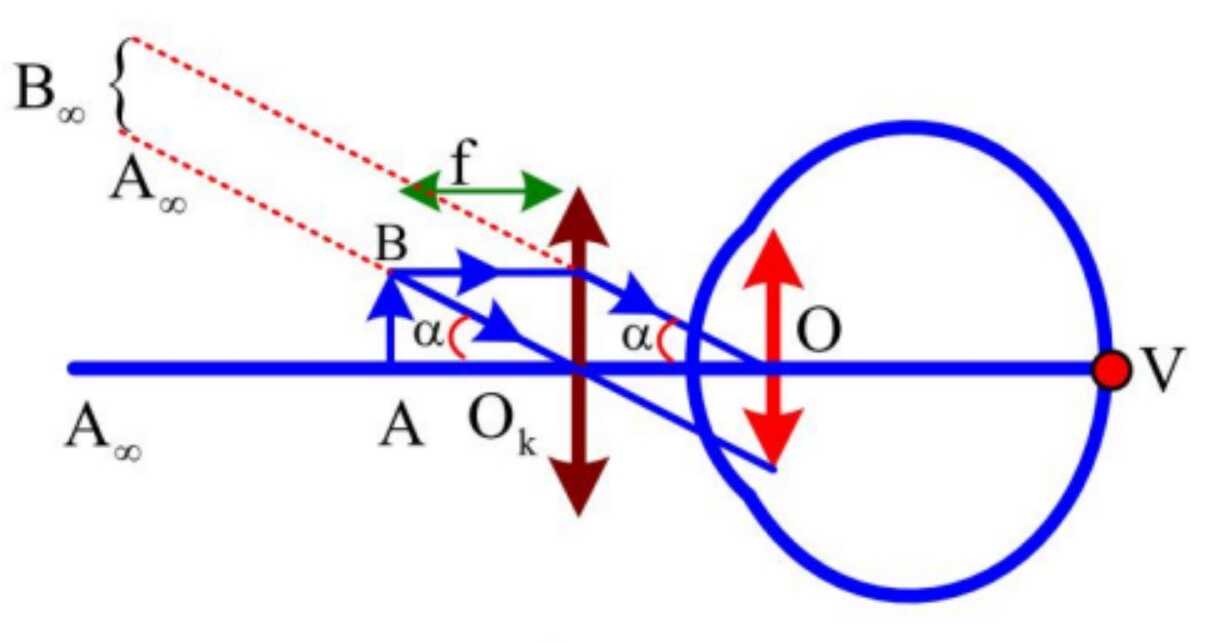
- Góc trông AB tại điểm cực cận:
- Góc trong ảnh A_{1}B_1:
- Số bội giác:
Đối d_M có 3 cách trường hợp sau:
\left\{\begin{matrix} d_M=OC_V & \\ d_M=OC_C& \\ d_M=\infty & \end{matrix}\right.
3 trường hợp d_M tương ứng với 3 trường hợp về số bội giác:
\left\{\begin{matrix} G_V=\frac{f-l+OC_V}{f}.\frac{OC_C}{OC_V} & \\ G_C=\left | k \right |& \\ G_\infty =\frac{OC_C}{f} & \end{matrix}\right.
- Trường hợp ngắm chừng ở vô cực:
\alpha = tan\alpha =\frac{AB}{f}
Số bội giác ở vô cực:
G_\infty =\frac{OC_C}{f}
2. Bài tập minh họa về số bội giác và góc trông
Để áp dụng được các công thức trên thì các bạn cần phải luyện tập, dưới đây là một số bài tập cực hay về bài toán số bội giác và góc trông có lời giải chi tiết để các bạn cùng tham khảo nhé!
Áp dụng công thức ta có:
\frac{25}{f}=5 \rightarrow f= 5(cm)
Số bội giác cả kính có trị số:
G_\infty =\frac{OC_C}{f}=\frac{20}{5}=4
Đối với bài này chúng ta có hai cách giải sau đây:
Cách 1:
Từ kí hiệu trên vành kính x10 ta có: \frac{25}{f}=10\rightarrow f=2,5 (cm)
Vì l= f nên độ bội giác trong trường hợp này luôn bằng:
G=\frac{OC_C}{f}=\frac{20}{2,5}= 8
Góc trông ảnh qua kính là:
\alpha =Gtan(\alpha _0)=G.\frac{AB}{OC_C}=8.\frac{1}{20}=0,4 (rad)
Cách 2:
Vì l=f nên tia tới từ B song song với trục chính cho tia ló đi qua F’
Góc trông có giá trị:
\alpha =tan (\alpha )=\frac{O_KC}{f}=\frac{1}{25}=0,4
Vì l=f nên tia tới từ B song song với trục chính cho tia ló đi qua F’
nên ta có công thức:
\alpha =\frac{O_KC}{f}=\frac{AB}{f}=AB.D
\rightarrow AB=\frac{\alpha }{D}=10^{-3} (m)
Tiêu cự của kính lúp:
f=\frac{1}{D}= 0,02 (m)= 2(cm)
Sơ đồ tạo ảnh là:
AB(d=d_C)\overset{O_1}{\rightarrow} A_1B_1(d_M=OC_C=5) \overset{Mat}{\rightarrow} V
Ta có:
d’=5- OC_C=-15\rightarrow k=\frac{d’-f}{-f}=\frac{-15-2}{-2}=8,5=G
Độ phóng đại ảnh bằng 6:
k=\frac{d’-f}{-f}\Leftrightarrow 6=\frac{d’-10}{-10}\rightarrow d’=-50 (cm)
Số bội giác là:
G=k.\frac{OC_C}{d_M}=k.\frac{OC_C}{-d’}=6.\frac{26}{2+50}=3
Như vậy, bài viết về Cách giải bài tập liên quan đến số bội giác và góc trông của HocThatGioi đến đây đã hết. Qua bài viết hi vọng sẽ giúp các bạn giải được các bài toán tương tự như trên. Đừng quên Like và Share để HocThatGioi ngày càng phát triên nhé. Cảm ơn các bạn đã theo dõi hết bài viết và chúc các bạn học tốt!