Tích của vec tơ với một số – Lý thuyết và bài tập có đáp án chi tiết nhất
Tích của vectơ với một số, điều kiện để hai vec tơ cùng phương hay phân tích một vec tơ thành hai vectơ không cùng phương là những kiến thức tuy cơ bản nhưng rất quan trọng trong chương trình Toán hình 10. Biết được điều đó, hôm nay HocThatGioi sẽ gửi đến các bạn bài viết Tích của vec tơ với một số – Lý thuyết và bài tập có đáp án chi tiết nhất để bạn đọc có thể nứm vững nội dung này nhé! Khám phá ngay thôi!

I. Lý thuyết tích của vec tơ với một số
1. Định nghĩa
Cho một số k \neq 0 và \overrightarrow{a} \neq 0.
Tích của một số k với vec tơ \overrightarrow{a} là một vec tơ , kí hiệu là k\overrightarrow{a}
- Cùng hướng với k\overrightarrow{a} nếu k>0
- Ngược hướng với k\overrightarrow{a} nếu k<0
- Có độ dài bằng |k||\overrightarrow{a}|
Quy ước: 0\overrightarrow{a}=0, k \overrightarrow{0} = \overrightarrow{0}
2. Tính chất
a) Phân phối với phép cộng vec tơ: k( \overrightarrow{a}+ \overrightarrow{b})=k \overrightarrow{a}+k \overrightarrow{b}
b) Phân phối với phép cộng các số: (h+k) \overrightarrow{a} =h \overrightarrow{a} +k \overrightarrow{a}
c) Kết hợp: h(k \overrightarrow{a} )=(hk) \overrightarrow{a}
d) 1 \overrightarrow{a} = \overrightarrow{a} ; -1 \overrightarrow{a} = -\overrightarrow{a}
3. Trung điểm đoạn thẳng và trọng tâm của tam giác
a) Nếu II là trung điểm của đoạn thẳng AB thì với mọi điểm M ta có: \overrightarrow{MA} + \overrightarrow{MB} =2 \overrightarrow{MI}
b) Nếu GG là trọng tâm của tam giác ABC thi mọi điểm M ta có: \overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} =3 \overrightarrow{MG}
4. Điều kiện để hai vec tơ cùng phương
Điều kiện cần và đủ để hai vec tơ \overrightarrow{a} và \overrightarrow{b} ( \overrightarrow{b} khác vec tơ 0) cùng phương là có một số k để \overrightarrow{a}=k \overrightarrow{b}
Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k khác 0 để \overrightarrow{AB}=k \overrightarrow{AC}
5. Phân tích một vec tơ thành hai vec tơ không cùng phương
Cho hai vec tơ \overrightarrow{a} và \overrightarrow{b} không cùng phương. Khi đó mọi vec tơ \overrightarrow{x} đều phân tích được một cách duy nhất theo hai vec tơ \overrightarrow{a}, \overrightarrow{b} nghĩa là có duy nhất một cặp số h,k sao cho \overrightarrow{x} =h \overrightarrow{a} +k \overrightarrow{b}
Khi đó ta nói vecto \overrightarrow{x} được phân tích (hay biểu thị) theo hai vecto không cùng phương là \overrightarrow{a}, \overrightarrow{b}
II. Bài tập SGK tích của vec tơ với một số
Bài 1 trang 17
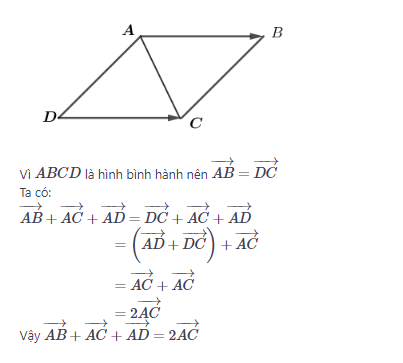
Bài 2 trang 17
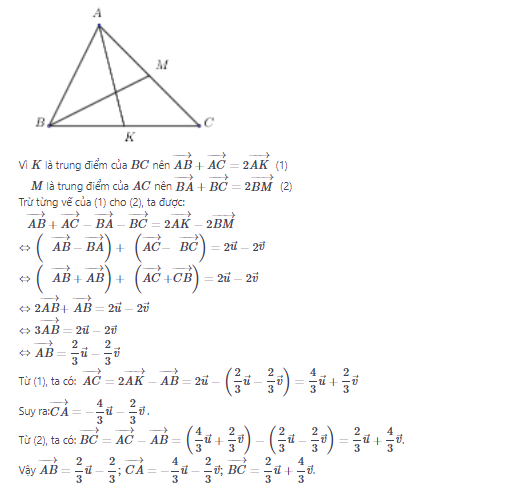
Bài 3 trang 17
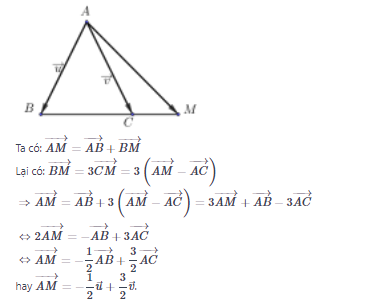
Bài 4 trang 17
a) 2 \overrightarrow{DA} + \overrightarrow{DB} + \overrightarrow{DC} = \overrightarrow{0}
b) 2 \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} = 4\overrightarrow{OD} với O là một điểm tùy ý

=> Xem thêm Tích vô hướng của hai vectơ – Lý thuyết và bài tập SGK có đáp án
Bài 5 trang 17
2 \overrightarrow{MN}= \overrightarrow{AC} + \overrightarrow{BD} = \overrightarrow{BC}+ \overrightarrow{AD}
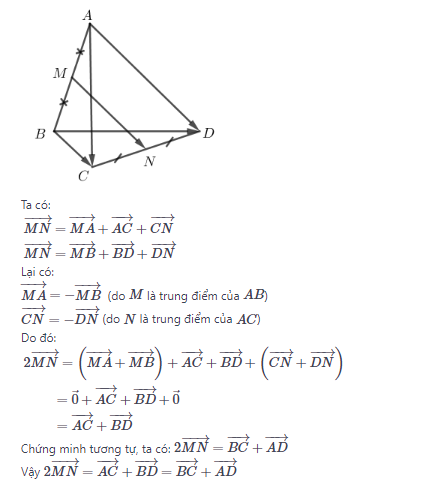
Bài 6 trang 17

Bài 7 trang 17
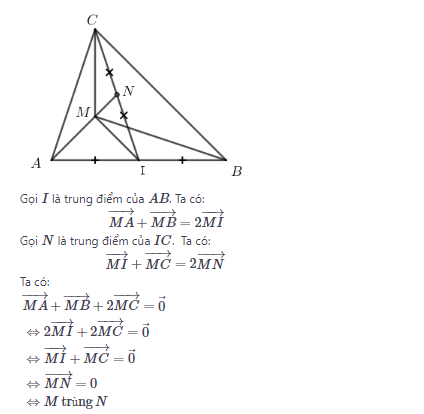
Bài 8 trang 17
Chứng minh rằng hai tam giác MNR và NQS có cùng trọng tâm.
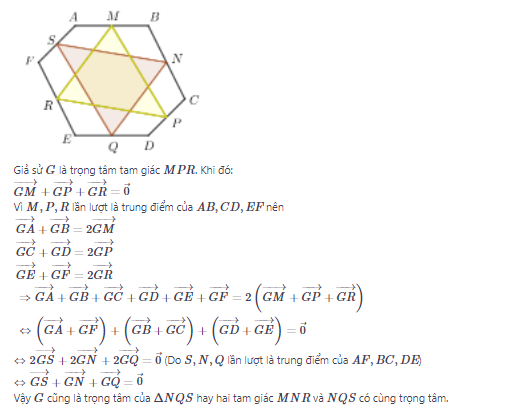
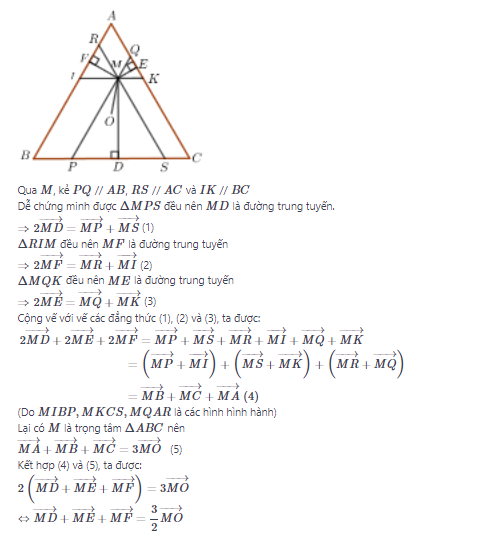
Bài 9 trang 17
Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng:
\overrightarrow{MD}+ \overrightarrow{ME} + \overrightarrow{MF} = \frac{3}{2}\overrightarrow{MO}
Trên đây là toàn bộ bài viết Tích của vec tơ với một số – Lý thuyết và bài tập có đáp án chi tiết nhất. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Hi vọng rằng bài viết sẽ mang lại thêm các kiến thức bổ ích cho các bạn. Hãy đồng hành cùng HocThatGioi để tiếp thu thêm các kiến thức hay, bổ ích nhé. Chúc các bạn học tốt!





