Chứng minh bất đẳng thức Cosi (Cauchy) cho mọi trường hợp cực dễ hiểu
Bất đẳng thức Cosi (Cauchy) là một bất đẳng thức khá nổi tiếng được ứng dụng trong nhiều bài toán về bất đẳng thức và cực trị. Bạn đã từng sử dụng bất đẳng thức này rất nhiều hay bạn vừa mới biết đến nó nhưng lại thắc mắc không biết tại sao nó lại đúng trong mọi trường hợp? Trong bài viết này, hãy cùng HocThatGioi đi chứng minh tính đúng đắn của bất đẳng thức này ở các trường hợp khác nhau nhé!
1. Chứng minh bất đẳng thức Cosi cho 2 số không âm
Ta thấy với a = 0 hoặc b = 0 thì bất đẳng thức luôn đúng. Vì vậy, chúng ta chỉ chứng minh bất đẳng thức Cosi với 2 số dương mà thôi.
a+b \geqslant 2\sqrt{ab}.
\Leftrightarrow a-2\sqrt{ab}+b \geqslant 0.
\Leftrightarrow (\sqrt a -\sqrt b)^2 \geqslant 0 (Luôn đúng vì a,b>0)
Vậy bất đẳng thức luôn đúng. (đpcm)
2. Chứng minh bất đẳng thức Cosi cho 3 số không âm
Với a = 0 hoặc b = 0 hoặc c = 0 thì bất đẳng thức luôn luôn đúng. Vì thế, chúng ta chỉ cần chứng minh bất đẳng thức Cosi với 3 số dương mà thôi.
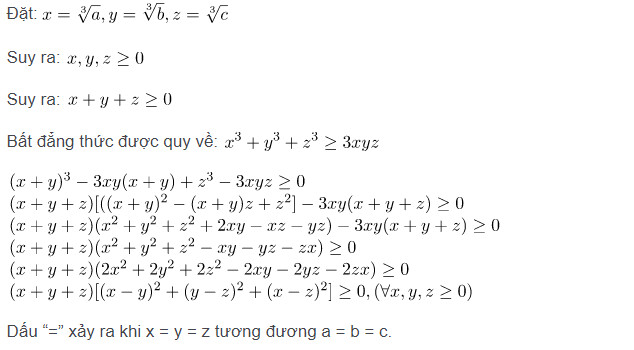
Vậy bất đẳng thức luôn đúng. (đpcm)
3. Chứng minh bất đẳng thức Cosi cho 4 số không âm
Với a = 0 hoặc b = 0 hoặc c = 0 hoặc d = 0 thì bất đẳng thức luôn đúng. Vì thế chúng ta cũng chỉ chứng minh bất đẳng thức cosi với 4 số dương mà thôi.
a+b+c+d \geqslant 4.\sqrt[4]{abcd}.
\Leftrightarrow (\frac{a+b+c+d}{4})^4 \geqslant abcd.
Thay d=\frac{a+b+c}{3} vào, ta được bất đẳng thức Cosi cho 3 số dương.
Vậy ta có được đpcm.
4. Chứng minh bất đẳng thức Cosi cho n số không âm
Chứng minh bất đẳng thức Cosi với n số dương
Ta có n=2 thì bất đẳng thức đúng.
Nếu bất đẳng thức đúng với n số thì nó cũng đúng với 2n số.
Ta có thể chứng minh đơn giản vì:
x_1+x_2+x_3+...+x_n \geqslant n.\sqrt[n]{x_1x_2x_3...x_n}+n.\sqrt[n]{x_{n+1}x_{n+2}...x_{2n}} \geqslant 2n.\sqrt[2n]{x_1x_2x_3…x_n}.
Theo quy nạp thì bất đẳng thức đúng với n là một lũy thừa của 2.
Mặt khác giả sử bất đẳng thức đúng với n số thì ta cũng chứng minh được nó đúng với n – 1 số như sau:
Theo bất đẳng thức cosi cho n số: x_1+x_2+x_3+...+x_n \geqslant n.\sqrt[n]{x_1x_2x_3...x_n}.
Chọn x_n=\frac{s}{n-1}, s=x_1+x_2+...x_n.
\Leftrightarrow s \geqslant (n-1).\sqrt[n-1]{x_1x_2x_3...x_{n-1}}.
Đây chính là bất đẳng thức cosi (n-1) số. Như vậy ta có đpcm.
5. Những quy tắc chung trong chứng minh bất đẳng thức sử dụng bất đẳng thức cosi
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Chứng minh bất đẳng thức Cosi. Hi vọng các bạn đã có thêm cho mình được những kiến thức bổ ích qua bài viết trên. Nếu thấy bài viết này hay, ý nghĩa hãy chia sẽ nó đến với bạn bè của mình để cùng nhau học thật giỏi nhé! Chúc các bạn học tốt!





