SGK Toán 10 - Chân Trời Sáng Tạo
Giải SGK Vẽ ba đường conic với Geogebra trang 92, 93, 94, 96 Toán 10 Chân trời sáng tạo
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi trong hoạt động thực hành trải nghiệm bài Vẽ ba đường conic bằng phần mềm Geogebra trang 92, 93, 94, 96. Hy vọng các bạn có thể tự mình thực hành được sau khi xem hết những bước thực hành cực chi tiết mà HocThatGioi trình bày ở dưới.
Thực hành 1 trang 92 Toán 10 Chân trời sáng tạo
Vẽ các elip sau:
a) $\frac{x^{2}}{10}+\frac{y^{2}}{4}=1$;
b) $\frac{x^{2}}{12}+\frac{y^{2}}{3}=1$;
c) $\frac{x^{2}}{100}+\frac{y^{2}}{36}=1$.
a) $\frac{x^{2}}{10}+\frac{y^{2}}{4}=1$;
b) $\frac{x^{2}}{12}+\frac{y^{2}}{3}=1$;
c) $\frac{x^{2}}{100}+\frac{y^{2}}{36}=1$.
Phương pháp giải:
Bước 1: Khởi động phần mềm Geogebra
Bước 2: Nhập phương trình elip $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ theo cú pháp $\mathrm{x}^{\wedge} 2 / \mathrm{a}^{\wedge} 2$ $+y^{\wedge} 2 / b^{\wedge} 2=1$ vào vùng nhập lệnh
Bước 3: Quan sát hình vẽ xuất hiện trên vùng làm việc
Bước 1: Khởi động phần mềm Geogebra
Bước 2: Nhập phương trình elip $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ theo cú pháp $\mathrm{x}^{\wedge} 2 / \mathrm{a}^{\wedge} 2$ $+y^{\wedge} 2 / b^{\wedge} 2=1$ vào vùng nhập lệnh
Bước 3: Quan sát hình vẽ xuất hiện trên vùng làm việc
Lời giải chi tiết:
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình elip theo cú pháp x^2/10 + y^2/4 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
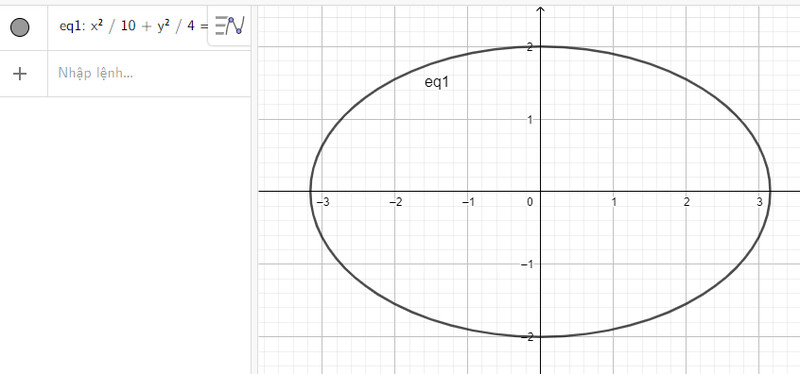
b) Nhập phương trình elip theo cú pháp x^2/12 + y^2/3 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
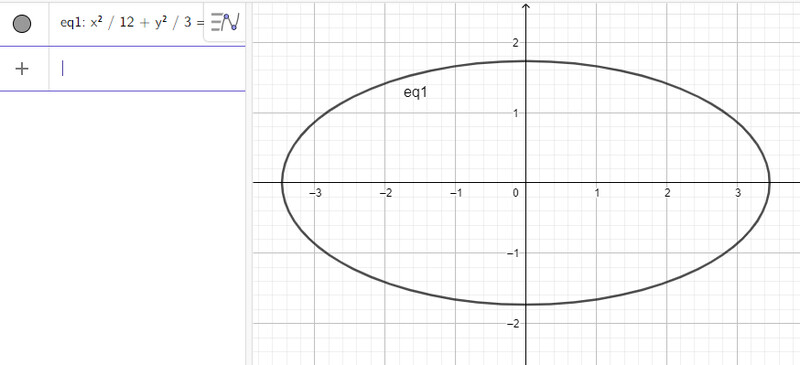
c) Nhập phương trình elip theo cú pháp x^2/100 + y^2/36 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
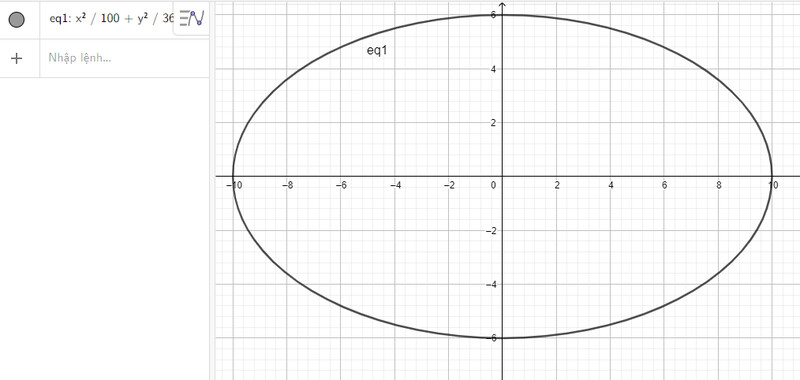
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình elip theo cú pháp x^2/10 + y^2/4 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:

b) Nhập phương trình elip theo cú pháp x^2/12 + y^2/3 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:

c) Nhập phương trình elip theo cú pháp x^2/100 + y^2/36 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:

Thực hành 2 trang 93 Toán 10 Chân trời sáng tạo
Thiết kế một đường hầm có mặt cắt hình nửa elip cao $4 \mathrm{~m}$ rộng $10 \mathrm{~m}$.
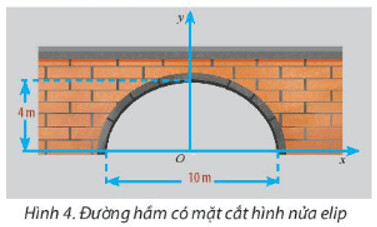

Phương pháp giải:
Từ chiều rộng và chiều cao xác định a, b. Từ đó xác định công thức elip và hình dạng
Từ chiều rộng và chiều cao xác định a, b. Từ đó xác định công thức elip và hình dạng
Lời giải chi tiết:
Ta có: Chiều cao và chiều rộng của đường hầm là $4 \mathrm{~m}, 10 \mathrm{~m}$ nên ta có: $a=5, b=4$
Nên phương trình chính tắc của elip có dạng $\frac{x^2}{25}+\frac{y^2}{16}=1$
Nhập phương trình elip theo cú pháp $x^{\wedge} 2 / 25+y^{\wedge} 2 / 16=1\{y>=0\}$
vào vùng nhập lệnh ta có hình vẽ mô phỏng đường hầm dưới đây
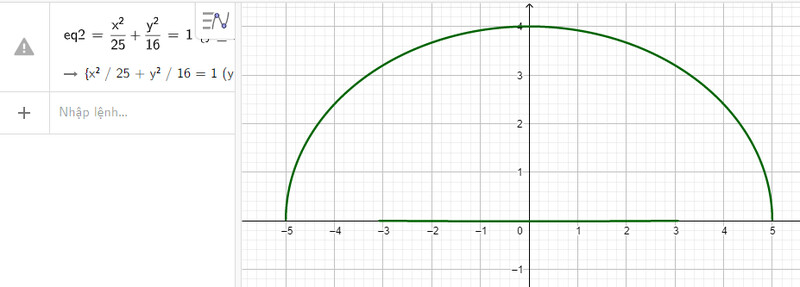
Vậy phương trình mô phỏng đường hầm là $\frac{x^2}{25}+\frac{y^2}{16}=1$ với $y \geq 0$ Và có hình mô phỏng thực tế như hình trên
Ta có: Chiều cao và chiều rộng của đường hầm là $4 \mathrm{~m}, 10 \mathrm{~m}$ nên ta có: $a=5, b=4$
Nên phương trình chính tắc của elip có dạng $\frac{x^2}{25}+\frac{y^2}{16}=1$
Nhập phương trình elip theo cú pháp $x^{\wedge} 2 / 25+y^{\wedge} 2 / 16=1\{y>=0\}$
vào vùng nhập lệnh ta có hình vẽ mô phỏng đường hầm dưới đây

Vậy phương trình mô phỏng đường hầm là $\frac{x^2}{25}+\frac{y^2}{16}=1$ với $y \geq 0$ Và có hình mô phỏng thực tế như hình trên
Thực hành 3 trang 94 Toán 10 Chân trời sáng tạo
Vẽ các hypebol sau:
a) $\frac{x^{2}}{10}-\frac{y^{2}}{6}=1$
b) $\frac{x^{2}}{4}-\frac{y^{2}}{3}=1$
c) $\frac{x^{2}}{64}-\frac{y^{2}}{36}=1$.
a) $\frac{x^{2}}{10}-\frac{y^{2}}{6}=1$
b) $\frac{x^{2}}{4}-\frac{y^{2}}{3}=1$
c) $\frac{x^{2}}{64}-\frac{y^{2}}{36}=1$.
Phương pháp giải:
Bước 1: Khởi động phần mềm Geogebra
Bước 2: Nhập phương trình hypebol $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ theo cú pháp $x^{\wedge} 2 / a^{\wedge} 2-y^{\wedge} 2 / b^{\wedge} 2=1$ vào vùng nhập lệnh
Bước 3: Quan sát hình vẽ xuất hiện trên vùng làm việc
Bước 1: Khởi động phần mềm Geogebra
Bước 2: Nhập phương trình hypebol $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ theo cú pháp $x^{\wedge} 2 / a^{\wedge} 2-y^{\wedge} 2 / b^{\wedge} 2=1$ vào vùng nhập lệnh
Bước 3: Quan sát hình vẽ xuất hiện trên vùng làm việc
Lời giải chi tiết:
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình hypebol theo cú pháp x^2/10 – y^2/6 = 1 vào vùng nhập lệnh ta được hình hypebpl dưới đây:
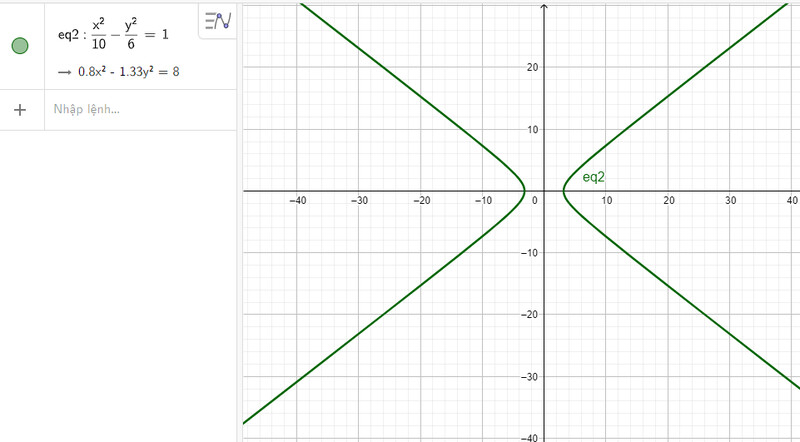
b) Nhập phương trình hypebol theo cú pháp x^2/4 – y^2/3 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:
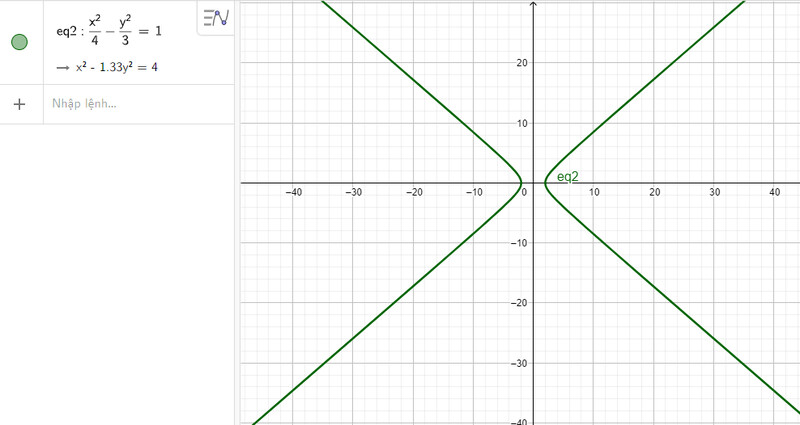
c) Nhập phương trình hypebol theo cú pháp x^2/64 – y^2/36 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:
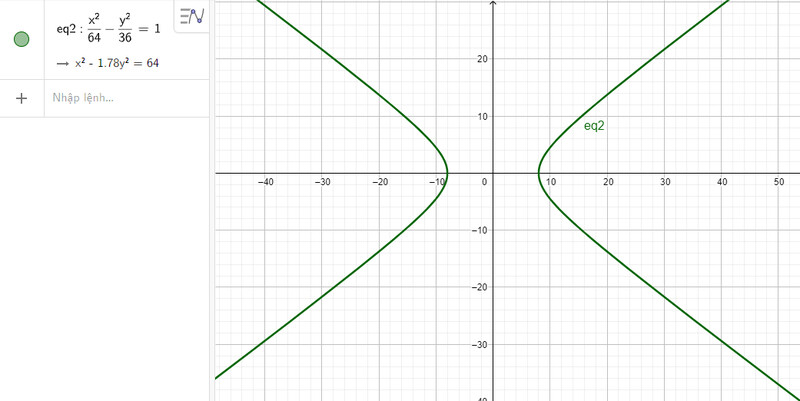
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình hypebol theo cú pháp x^2/10 – y^2/6 = 1 vào vùng nhập lệnh ta được hình hypebpl dưới đây:

b) Nhập phương trình hypebol theo cú pháp x^2/4 – y^2/3 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:

c) Nhập phương trình hypebol theo cú pháp x^2/64 – y^2/36 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:

Thực hành 4 trang 96 Toán 10 Chân trời sáng tạo
Vẽ các parabol sau:
a) $y^{2}=16 x$
b) $y^{2}=x$
c) $y^{2}=32 x$.
a) $y^{2}=16 x$
b) $y^{2}=x$
c) $y^{2}=32 x$.
Phương pháp giải:
Bước 1: Khởi động phần mềm Geogebra
Bước 2: Nhập phương trình parabol $y^2=2 p x$ theo cú pháp $\mathrm{y}^{\wedge} 2=$ $2 p x$ vào vùng nhập lệnh
Bước 3: Quan sát hình vẽ xuất hiện trên vùng làm việc
Bước 1: Khởi động phần mềm Geogebra
Bước 2: Nhập phương trình parabol $y^2=2 p x$ theo cú pháp $\mathrm{y}^{\wedge} 2=$ $2 p x$ vào vùng nhập lệnh
Bước 3: Quan sát hình vẽ xuất hiện trên vùng làm việc
Lời giải chi tiết:
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình parabol theo cú pháp y^2 = 16x vào vùng nhập lệnh ta được hình parabol dưới đây:
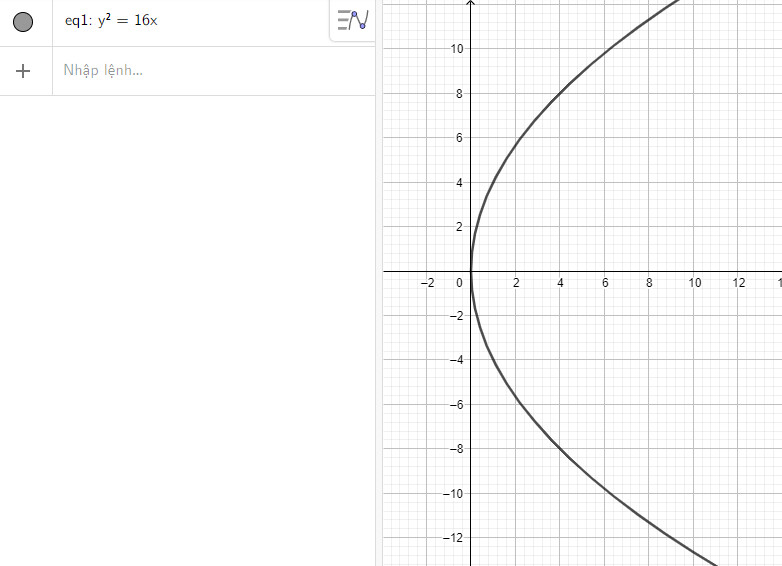
b) Nhập phương trình parabol theo cú pháp y^2 = x vào vùng nhập lệnh ta được hình parabol dưới đây:
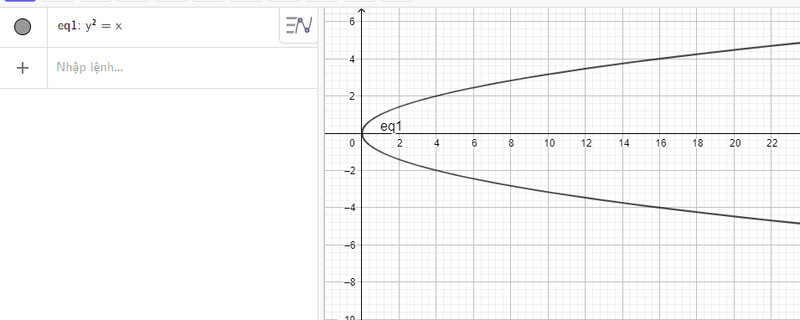
c) Nhập phương trình parabol theo cú pháp y^2 = 32x vào vùng nhập lệnh ta được hình parabol dưới đây:
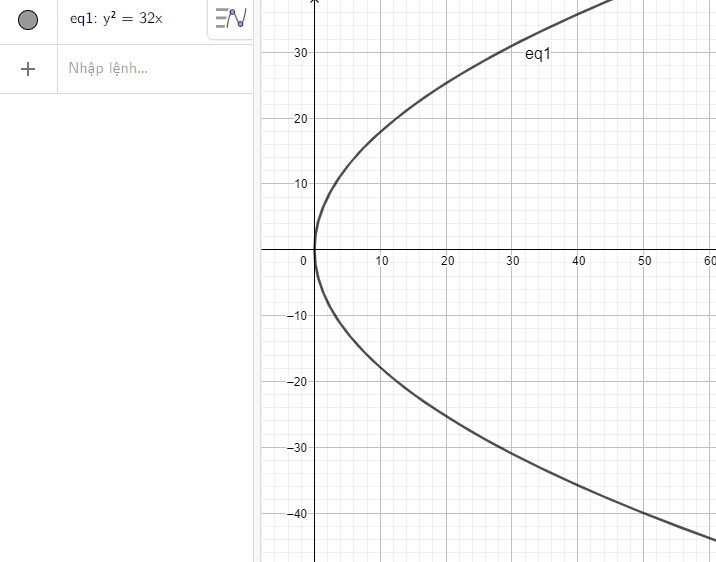
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình parabol theo cú pháp y^2 = 16x vào vùng nhập lệnh ta được hình parabol dưới đây:

b) Nhập phương trình parabol theo cú pháp y^2 = x vào vùng nhập lệnh ta được hình parabol dưới đây:

c) Nhập phương trình parabol theo cú pháp y^2 = 32x vào vùng nhập lệnh ta được hình parabol dưới đây:

Thực hành 5 trang 96 Toán 10 Chân trời sáng tạo
Thiết kế một chóa đèn có mặt cắt hình parabol với kích thước được cho trong hình sau:
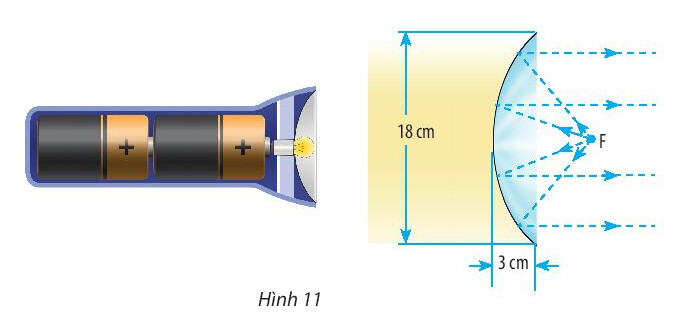

Phương pháp giải:
Bước 1: Giả sử phương trình của parabol
Bước 2: Từ kích thước giả thiết cho, xác định điểm nằm trên phương trình
Bước 3: Xác định phương trình parabol
Bước 4: Sử dụng Geogebra vẽ hình dạng mô phỏng chóa đèn
Bước 1: Giả sử phương trình của parabol
Bước 2: Từ kích thước giả thiết cho, xác định điểm nằm trên phương trình
Bước 3: Xác định phương trình parabol
Bước 4: Sử dụng Geogebra vẽ hình dạng mô phỏng chóa đèn
Lời giải chi tiết:
Chóa đèn có hình dạng parabol nên phương trình mô phỏng chóa đèn có dạng $y^2=2 p x$
Gắn hệ tọa độ $O x y$ vào chóa đèn với gốc tọa độ tại đỉnh chóa đèn, suy ta phương trình đó đi qua điểm có tọa độ $(3 ; 9)$
Thay tọa độ điểm $(3 ; 9)$ vào phương trình $y^2=2 p x$, ta có $9^2=2 p .3 \Rightarrow p=\frac{27}{2}$
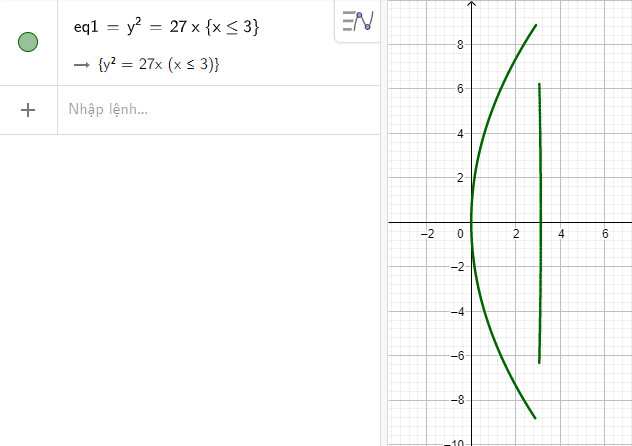
Suy ra phương trình mô tả chóa đèn là $y^2=27 x$ với $x \leq 3$
Hình ảnh mô phỏng chóa đèn có dạng như hình dưới:
Chóa đèn có hình dạng parabol nên phương trình mô phỏng chóa đèn có dạng $y^2=2 p x$
Gắn hệ tọa độ $O x y$ vào chóa đèn với gốc tọa độ tại đỉnh chóa đèn, suy ta phương trình đó đi qua điểm có tọa độ $(3 ; 9)$
Thay tọa độ điểm $(3 ; 9)$ vào phương trình $y^2=2 p x$, ta có $9^2=2 p .3 \Rightarrow p=\frac{27}{2}$
Suy ra phương trình mô tả chóa đèn là $y^2=27 x$ với $x \leq 3$
Hình ảnh mô phỏng chóa đèn có dạng như hình dưới:

Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK Vẽ ba đường conic với Geogebra trang 92, 93, 94, 96 Toán 10 Chân trời sáng tạo. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





