Giải SGK bài 3 trang 16,17,18,19 Toán 7 Kết nối tri thức tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Lũy thừa với số mũ tự nhiên của một số hữu tỉ. Các bài tập sau đây thuộc bài 3 chương 1 trang 16,17,18,19. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK trang 16,17,18 Toán 7 kết nối tri thức tập 1
Các hoạt động khám phá, thực hành, vận dụng luyện tập ở các trang 16, 17, 18 SGK Toán 7 Kết nối tri thức tập 1 này sẽ giúp các bạn đi vào bài học tìm hiểu các kiến thức về Lũy thừa với số mũ tự nhiên của một số hữu tỉ một cách trơn tru và dễ hiểu hơn rất nhiều đấy! Cùng xem lời giải của HocThatGioi nhé!
Mở đầu trang 16
(Theo usgs.gov)
Muốn biết lượng nước trên Trái Đất là khoảng bao nhiêu kilômét khối, ta cẩn tính $1111,34 \times 1111,34 \times 1111,34$. Biểu thức này có thể viết gọn hơn dưới dạng luȳ thừa giống như luȳ thừa của một số tự nhiên mà em đã học ở lớp 6.
Sau khi học xong bài này, chúng ta sẽ giải được câu hỏi trên như sau:
$1111,34 × 1111,34 × 1111,34 = 1111,343.$
HĐ1 trang 16
a) $2 \cdot 2 \cdot 2 \cdot 2$;
b) $5 \cdot 5 \cdot 5$
$a.a….a$ ($n $ thừa số $a$) $=a^n$ Ở đó:
$a$: cơ số
$n$: số mũ
a) $2.2.2.2 = 2 4$ . Cơ số $2$ , số mũ $4$
b) $5.5 .5=5^3$. Cơ số $5$ , số mũ $3$
HĐ2 trang 16
a) $(-2) \cdot(-2) \cdot(-2)$;
b) $(-0,5) \cdot(-0,5)$;
c) $\frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2}$
Thực hiện phép nhân các số hữu tỉ
a) $(-2) \cdot(-2) \cdot(-2)=4 \cdot(-2)=-8$
b) $(-0,5) \cdot(-0,5)=0,25$
c)
$ \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} $
$ =\frac{1 \cdot 1 \cdot 1 \cdot 1}{2 \cdot 2 \cdot 2 \cdot 2} $
$ =\frac{1}{16}$
HĐ3 trang 16
$a.a….a$ ($n$ thừa số $a$) $=a^n$
a) $(-2) \cdot(-2) \cdot(-2)=(-2)^3$
b) $(-0,5) \cdot(-0,5)=(-0,5)^2$
c) $\frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2}=\left(\frac{1}{2}\right)^4$
Luyện tập 1 trang 17
a) $\left(-\frac{4}{5}\right)^{4}$
b) $(0,7)^{3}$.
$a.a….a$ ($n$ thừa số $a$) $=a^n$
a) $\left(-\frac{4}{5}\right)^4=\left(-\frac{4}{5}\right) \cdot\left(-\frac{4}{5}\right) \cdot\left(-\frac{4}{5}\right) \cdot\left(-\frac{4}{5}\right) $
$=\frac{16}{25} \cdot \frac{16}{25} $
$ =\frac{256}{625} $
$ \text { b) }(0,7)^3=0,7 \cdot 0,7.0,7 $
$ =0,49.0,7 $
$ =0,343
Luyện tập 2 trang 17
a) $\left(\frac{2}{3}\right)^{10} \cdot 3^{10}$
b) $(-125)^{3}: 25^{3}$;
c) $(0,08)^{3} \cdot 10^{6}$.
$ a^n=\text { a.a…a (n thừa số a) } $
$ (x \cdot y)^n=x^n \cdot y^n $
$ \left(\frac{x}{y}\right)^n=\frac{x^n}{y^n}$
a) $\left(\frac{2}{3}\right)^{10} \cdot 3^{10}=\frac{2^{10}}{3^{10}} \cdot 3^{10}=2^{10}$
b) $(-125)^3: 25^3=(-125: 25)^3=(-5)^3=-125$
c) $(0,08)^3 \cdot 10^6=(0,08)^3 \cdot 100^3=(0,08.100)^3=8^3$
Vận dụng trang 17
Công thức tính thể tích hình lập phương cạnh a là:
$\mathrm{V}=\mathrm{a} \cdot \mathrm{a} \cdot \mathrm{a}=a^3$
Biểu thức lũy thừa tính toàn bộ lượng nước trên Trái Đất trong bài toán mở đầu (đơn vị kilomét khối) là:
$V=(1111,34)^3$
HĐ4 trang 17
a) $(-3)^{2} \cdot(-3)^{4}$ và $(-3)^{2+4}$
b) $0,6^{3}: 0,6^{2}$ và $0,6^{3-2}$.
Tính dựa vào định nghĩa lũy thừa.
a)
$ (-3)^2 \cdot(-3)^4=9.81=729 $
$ (-3)^6=(-3) \cdot(-3) \cdot(-3) \cdot(-3) \cdot(-3) \cdot(-3) $
$ =9.9 \cdot 9=729 $
$ \text { Vậy }(-3)^2 \cdot(-3)^4=(-3)^6$
b)
$0,6^3: 0,6^2=0,216: 0,36=0,6$
Vậy $0,6^3: 0,6^2=0,6$
Luyện tập 3 trang 18
a) $(-2)^{3} \cdot(-2)^{4}$
b) $(0,25)^{7}:(0,25)^{3}$.
Sử dụng công thức tích và thương của lũy thừa có cùng cơ số:
$ x^m \cdot x^n=x^{m+n} $
$ x^m: x^n=x^{m-n}(x \neq 0 ; m \geq n)$
$a)(-2)^3 \cdot(-2)^4=(-2)^{3+4}=(-2)^7$
$b)(0,25)^7:(0,25)^3=(0,25)^{7-3}=(0,25)^4$
HĐ5 trang 18
Sử dụng định nghĩa lũy thừa và công thức tích các lũy thừa có cùng cơ số
Ta có:
$\left(2^2\right)^3=2^2 \cdot 2^2 \cdot 2^2=2^{2+2+2}=2^6$
$\left[(-3)^2\right]^2=(-3)^2 \cdot(-3)^2=(-3)^{2+2}=(-3)^4$
Luyện tập 4 trang 18
+ Bước 1: Viết các số $\frac{1}{4} ; \frac{1}{8}$ dưới dạng Iũy thừa cơ số $\frac{1}{2}$
+ Bước 2: Sử dụng công thức lũy thừa của lũy thừa:$\left(x^m\right)^n=x^{mn}$
Ta có:
$ \left(\frac{1}{4}\right)^8=\left[\left(\frac{1}{2}\right)^2\right]^8=\left(\frac{1}{2}\right)^{2.8}=\left(\frac{1}{2}\right)^{16} $
$ \left(\frac{1}{8}\right)^3=\left[\left(\frac{1}{2}\right)^3\right]^3=\left(\frac{1}{2}\right)^{3.3}=\left(\frac{1}{2}\right)^9$
Thử thách nhỏ trang 18
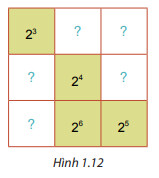
Tính tích của 3 ô in đậm ở đường chéo đã biết. Tích này chính là tích của từng hàng , cột.
Tính hàng, cột khi biết tích của hàng, cột và 2 ô của hàng, cột đó.
Ta đặt các ô chưa biết như sau:
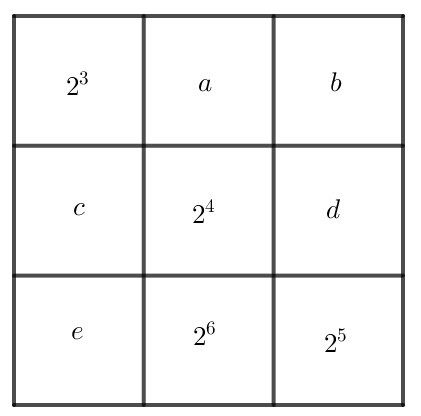
Ta có:
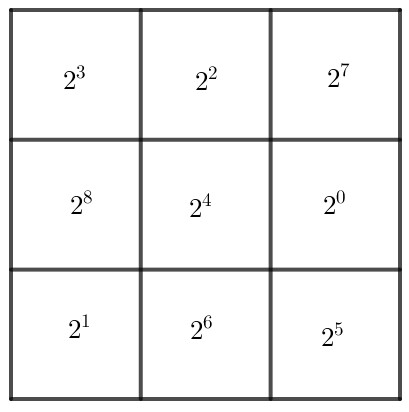
Tích của mỗi hàng, cột, đường chéo bằng: $2^3 \cdot 2^4 \cdot 2^5=2^{3|4| 5}=2^{12}$
$ a=2^{12}: 2^6: 2^5=2^{12-6-5}=2^1=2 $
$ b=2^{12}: 2^1: 2^3=2^{12-1-3}=2^8 $
$ c=2^{12}: 2^8: 2^4=2^{12-8-4}=2^0=1 $
$ d=2^{12}: 2^0: 2^5=2^{12-0-5}=2^7 $
$ e=2^{12}: 2^7: 2^3=2^{12-7-3}=2^2$
Vậy ta có bảng hoàn chỉnh là:
Giải bài tập SGK trang 18,19 Toán 7 kết nối tri thức tập 1
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Lũy thừa với số mũ tự nhiên của một số hữu tỉ trang 18,19 sách Toán 7 kết nối tri thức tập 1 dưới đây nhé!
Bài 1.18 trang 18
Biểu diễn các số dưới dạng tích các thừa số 5 rồi sử dụng định nghĩa lũy thừa: $a . a . .. a=a^n$ ( $n$ thừa số a)
Ta có:
$125=5.5 .5=5^3 $
$3125=5.5 .5 .5 .5=5^5$
Bài 1.19 trang 18
+ Bước 1 : Viết các số $\frac{1}{9} ; \frac{1}{27}$ dưới dạng lũy thừa cơ số $\frac{1}{3}$
+ Bước 2: Sử dụng công thức lũy thừa của lũy thừa: $\left(x^m\right)^n=x^{m \cdot n}$
Ta có:
$ \left(\frac{1}{9}\right)^5=\left[\left(\frac{1}{3}\right)^2\right]^5=\left(\frac{1}{3}\right)^{2.5}=\left(\frac{1}{3}\right)^{10} $
$ \left(\frac{1}{27}\right)^7=\left[\left(\frac{1}{3}\right)^3\right]^7=\left(\frac{1}{3}\right)^{3.7}=\left(\frac{1}{3}\right)^{21}$
Bài 1.20 trang 18

Ô tiếp theo là tích của hai lũy thừa ở hai ô liền trước.
Sử dụng công thức tích của lũy thừa có cùng cơ số: $x^m \cdot x^n=x^{m+n}$
Ta có:
$ 3^0 \cdot 3^1=3^{0+1}=3^1 $
$ 3^1 \cdot 3^1=3^{1+1}=3^2 $
$ 3^1 \cdot 3^2=3^{1+2}=3^3 $
$ 3^2 \cdot 3^3=3^{2+3}=3^5 $
$ 3^3 \cdot 3^5=3^{3+5}=3^8$
Vậy ta được:

Bài 1.21 trang 19
a) $(-3)^{8}$, biết $(-3)^{7}=-2187$
b) $\left(-\frac{2}{3}\right)^{12}$, biết $\left(-\frac{2}{3}\right)^{11}=\frac{-2048}{177147}$.
Sử dụng: $ x^m=x^{m-1} . x$
a) $(-3)^8=(-3)^7 \cdot(-3)=-2187 \cdot(-3)=6561$
b) $\left(-\frac{2}{3}\right)^{12}=\left(-\frac{2}{3}\right)^{11} \cdot\left(-\frac{2}{3}\right)=\frac{-2048}{177147} \cdot \frac{-2}{3}=\frac{4096}{531441}$
Bài 1.22 trang 19
a) $15^{8} \cdot 2^{4}$
b) $27^{5}: 32^{3}$.
Bước 1 : Đưa về dạng 2 lũy thừa có cùng số mũ
Bước 2: Áp dụng công thức tích, thương của 2 lũy thừa có cùng số mũ:
$a^n \cdot b^n=(a . b)^n ; a^n: b^n=(a: b)^n$
a)$ 15^8 \cdot 2^4=15^{2.4} \cdot 2^4=\left(15^2\right)^4 \cdot 2^4 $
$ =225^4 \cdot 2^4=(225 \cdot 2)^4=450^4 $
$ b) 27^5: 32^3=\left(3^3\right)^5:\left(2^5\right)^3 $
$ =3^{3.5}: 2^{5.3}=3^{15}: 2^{15}=\left(\frac{3}{2}\right)^{15}$
Bài 1.23 trang 19
a) $\left(1+\frac{1}{2}-\frac{1}{4}\right)^{2} \cdot\left(2+\frac{3}{7}\right)$
b) $4:\left(\frac{1}{2}-\frac{1}{3}\right)^{3}$.
Thực hiện phép tính trong ngoặc rồi tính lũy thừa, sau đó thực hiện phép nhân ( chia)
a)
$ \left(1+\frac{1}{2}-\frac{1}{4}\right)^2 \cdot\left(2+\frac{3}{7}\right) $
$ =\left(\frac{4}{4}+\frac{2}{4}-\frac{1}{4}\right)^2 \cdot\left(\frac{14}{7}+\frac{3}{7}\right) \$
$ =\left(\frac{5}{4}\right)^2 \cdot \frac{17}{7} $
$ =\frac{25}{16} \cdot \frac{17}{7} $
$ =\frac{425}{112}$
b)
$ 4:\left(\frac{1}{2}-\frac{1}{3}\right)^3 $
$ =4:\left(\frac{3}{6}-\frac{2}{6}\right)^3 $
$ =4:\left(\frac{1}{6}\right)^3 $
$ =4: \frac{1}{216} $
$ =4.216$
$ =864$
Bài 1.24 trang 19
(Theo solarsystem.nasa.gov)
Thực hiện phép chia 2 khoảng cách.
Khoảng cách từ Mộc tinh đến Mặt Trời gấp khoảng số lần khoảng cách từ Trái Đất đến Mặt Trời là:
$\frac{7,78.10^8}{1,5.10^8}=\frac{7,78}{1,5} \approx 5,2 \text { (lần) }$
Bài 1.25 trang 19
Em hãy sắp xếp tên các quốc gia theo thứ tự số lượng khách đến thăm Việt Nam từ nhỏ đến lớn.
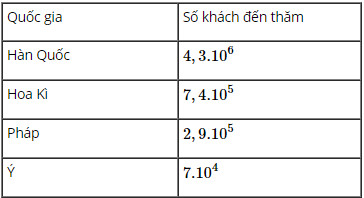
Đưa các số liệu về dạng $ a .10^4 $ rồi so sánh
Ta có: $4,3.10^6=430.10^4$;
$ 7,4.10^5=74.10^4 ; $
$ 2,9.10^5=29.10^4 $
$ \mathrm{Vi} 7<29<74<430 \text { nên } $
$ 7.10^4<29.10^4<74.10^4<430.10^4$
Vậy các quốc gia theo thứ tự số lượng khách đến thăm Việt Nam từ nhỏ đến lớn là: Ý, Pháp, Hoa Kì, Hàn Quốc.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 3 – Lũy thừa với số mũ tự nhiên của một số hữu tỉ trang 16,17,18,19 Toán 7 Kết nối tri thức tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





