Giải SGK bài 6 trang 29,30,31,32 Toán 7 Kết nối tri thức tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Số vô tỉ. Căn bậc hai số học. Các bài tập sau đây thuộc bài 6 chương 2 – Số thực trang 29, 30, 31, 32 SGK Toán 7 Kết nối tri thức. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK trang 29, 30 Toán 7 Kết nối tri thức tập 1
Những lời giải dưới đây sẽ giúp bạn đi tìm đáp án cho các hoạt động, câu hỏi và luyện tập ở các trang 29, 30 trong bài Số vô tỉ. Căn bậc hai số học một cách nhanh chóng và dễ hiểu. Cùng theo dõi ngay nhé!
Hoạt động 1 trang 29
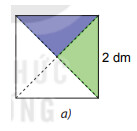
Cắt theo mô tả của đề bài
Bước 1: Cắt một hình vuông cạnh bằng 2 dm
Bước 2: Cắt hình vuông thành bốn tam giác vuông bằng nhau dọc theo hai đường chéo của hình vuông.
Hoạt động 2 trang 29
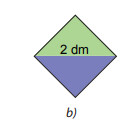
Ghép 2 tam giác như hình.
Diện tích hình vuông = Diện tích hình vuông ban đầu (cạnh 2 dm) : 2
Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông.
Vì 2 tam giác vuông chiếm một nửa hình vuông ban đầu nên
Diện tích hình vuông thu được là:
$2.2:2= 2 (dm^2)$
Hoạt động 3 trang 29
Bước 1: Dùng thước đo cạnh hình vuông nhận được trong HĐ2, ta được số liệu có đơn vị cm.
Bước 2: Đổi đơn vị cm sang dm.
Dùng thước đo ta được cạnh hình vuông dài khoảng $14 cm$.
Ta có: $14 cm = 1,4 dm$
Vận dụng trang 30
Từ công thức tính chu vi đường tròn: $\mathrm{C}=\pi \cdot \mathrm{d} a=\sqrt{S} \Rightarrow d=\frac{C}{\pi}$ Thực hiện theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”
Theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”, có:
$d=\frac{C}{8} \cdot 5: 2=\frac{C}{8} \cdot 5 \cdot \frac{1}{2}=\frac{5 C}{16}=\frac{C}{\frac{16}{5}}$
Theo công thức, có: $d=\frac{C}{\pi}$
Như vậy, người xưa đã ước lượng số $\pi$ bằng $\frac{16}{5}=3,2$.
Luyện tập 1 trang 30
b) $\sqrt{81}$;
c) $\sqrt{2021^{2}}$
$\sqrt{a}=x $ thì ta có: $ a=x^2(x \geq 0)$
a) $V i 4^2=16$ nên $\sqrt{16}=4$
b) Vi $9^2=81$ nên $\sqrt{81}=9$
c) Vi $2021>0$ nên $\sqrt{2021^2}=2021$
Vận dụng 1 trang 30
Tìm cạnh a của hình vuông có diện tích S: $a=\sqrt{S}$ Tính chu vi hình vuông cạnh a là: $C=4 . a$
Cạnh của sàn thi đấu là: $\sqrt{144}=12(\mathrm{~m})$
Chu vi của sàn thi đấu là: $4.12=48(\mathrm{~m})$
Luyện tập 2 trang 31
a) $\sqrt{15}$
b) $\sqrt{2,56}$;
c) $\sqrt{17256}$;
d) $\sqrt{793881}$.
+ Bước 1: Bấm máy tính, tính các căn bậc hai.
+ Bước 2: Xác định hàng làm tròn.
+ Bước 3: Làm tròn theo quy tắc làm tròn số thập phân.
– Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5
– Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân
+ Thay bằng các chữ số 0 nếu ở phần số nguyên
Độ chính xác 0,005 tức là ta cần làm tròn đến hàng phần trăm
a) $\sqrt{15}=3,8729 \ldots \approx 3,87$
b) $\sqrt{2,56}=1,6$
c) $\sqrt{17256}=131,3620 \ldots \approx 131,36$
d) $\sqrt{793881}=891$
Vận dụng 2 trang 31
(Theo khoahoc.tv)
Biết rằng đáy của kim tự tháp Kheops có dạng một hình vuông. Tính độ dài cạnh đáy của kim tự tháp này (làm tròn kết quả đến chữ số thập phân thứ nhất).
Tính cạnh a của hình vuông có diện tích S: $a=\sqrt{S}$ Làm tròn theo quy tắc làm tròn số thập phân.
– Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5
– Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên
Độ dài cạnh đáy của kim tự tháp này là: $\sqrt{52198,16} \approx 228,469(\mathrm{~m})$ Làm tròn đến chữ số thập phân thứ nhất, ta được: $228,5 \mathrm{~m}$ (vì chữ số ở hàng làm tròn là 4 , chữ số ngay sau hàng làm tròn là $6>5$ nên ta tăng 1 đơn vị ở hàng làm tròn, đồng thời bỏ đi các chữ số ở sau hàng làm tròn)
Giải bài tập SGK trang 32 Toán 7 Kết nối tri thức tập 1
Những bài tập SGK ở cuối bài Số vô tỉ. Căn bậc hai số học trang 32 Toán 7 kết nối tri thức sẽ giúp các bạn vận dụng những kiến thức vừa học để giải các bài tập từ cơ bản đến nâng cao. Cùng HocThatGioi giải quyết những bài toán này nhé!
Bài 2.6 trang 32
$x^2=a$ và $x$ không âm thì $\sqrt{a}=x$
Vi $23409=153^2$ và $153>0$ nên $\sqrt{23409}=153$
Bài 2.7 trang 32
a) 9 ;
b) 16 ;
c) 81 ;
d) 121 .
$x^2=a \text { thì } \sqrt{a}=x(\mathrm{x}>0)$
a) Vi $3^2=9$ và $3>0$ nên $\sqrt{9}=3$
b) Vi $4^2=16$ và $4>0$ nên $\sqrt{16}=4$
c) Vì $9^2=81$ và $9>0$ nên $\sqrt{81}=9$
d) Vi $11^2=121$ và $11>0$ nên $\sqrt{121}=11$
Bài 2.8 trang 32
Vì $324=2^{2} \cdot 3^{4}=\left(2 \cdot 3^{2}\right)^{2}=18^{2}$ nên $\sqrt{324}=18$
Tính căn bậc hai số học của 129600 .
Phân tích $129600$ ra thừa số nguyên tố, rồi đưa về dạng $a^2$
Ta có: $129600=2^6 .3^4 \cdot 5^2=\left(2^3 .3^2 \cdot 5\right)^2=360^2$ nên $\sqrt{129600}=360$
Bài 2.9 trang 32
a) $81 \mathrm{dm}^{2}$;
b) $3600 \mathrm{~m}^{2}$;
c) $1 \mathrm{ha}$.
Tìm căn bậc hai số học của một số.
Chú ý đơn vị.
a) Độ dài các cạnh của hình vuông là: $\sqrt{81}=9(\mathrm{dm})$
b) Độ dài các cạnh của hình vuông là: $\sqrt{3600}=60(\mathrm{~m})$
c) Đổi 1 ha $=10000 \mathrm{~m}^2$
Độ dài các cạnh của hình vuông là: $\sqrt{10000}=100$ (m)
Bài 2.10 trang 32
a) $81 \mathrm{dm}^{2}$;
b) $3600 \mathrm{~m}^{2}$;
c) $1 \mathrm{ha}$.
* Bấm máy tính tìm căn bậc hai số học.
* Làm tròn theo quy tắc làm tròn số thập phân.
– Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5
– Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên
Làm tròn các kết quả với độ chính xác 0,005 tức là làm tròn đến hàng phần trăm.
a) $\sqrt{3}=1,73205 \ldots \approx 1,73$
b) $\sqrt{41}=6,40312 \ldots \approx 6,40$
c) $\sqrt{2021}=44,95553 \ldots \approx 44,96$
Bài 2.11 trang 32
Bước 1: Tính tổng các bình phương độ dài hai cạnh của hình chữ nhật.
Bước 2: Tìm căn bậc hai số học của tổng vừa tìm được bằng máy tính cầm tay
Bước 3: Làm tròn kết quả đến hàng phần mười.
Ta có: Bình phương độ dài đường chéo của một hình chữ nhật là: $5^2+8^2=25+64=89$
Độ dài đường chéo của một hình chữ nhật là: $\sqrt{89}=9,43398 \ldots(\mathrm{dm})$
Làm tròn kết quả này đến hàng phần mười, ta được: 9,4 $\mathrm{dm}$
Chú ý: Độ dài đường chéo của một hình chữ nhật bằng căn bậc hai số học của tổng các bình phương độ dài hai cạnh của nó
Bài 2.12 trang 32
Bước 1: Tìm diện tích 1 viên gạch
Bước 2: Đổi các số liệu về cùng đơn vị
Bước 3: Tìm số viên gạch
Diện tích 1 viên gạch là: $50^2=2500\left(\mathrm{~cm}^2\right)=0,25 \mathrm{~m}^2$.
Số viên gạch cần là: $100: 0,25=400$ (viên)
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 6 –Số vô tỉ. Căn bậc hai số học trang 29,30,31,32 Toán 7 Kết nối tri thức tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





