Giải SGK Bài 16 trang 80, 81, 82, 83, 84 SGK Toán 7 Kết nối tri thức Tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết tất cả các câu hỏi, vận dụng, luyện tập và bài tập và cùng nhau tìm ra phương pháp giải hay, nhanh nhất cho bài Tam giác cân. Đường trung trực của đoạn thẳng. Các bài tập sau đây thuộc Bài 16 chương 3 trang 81, 82, 83, 84 Toán 7 Kết nối tri thức Tập 1. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Giải mục 1 SGK trang 80, 81 Toán 7 Kết nối tri thức tập 1
Cùng HocThatGioi tìm ra đáp án chính xác nhất cho các câu hỏi, luyện tập và vận dụng ở các trang 80, 81, 82, 83, 84 trong bài Tam giác cân. Đường trung trực của đoạn thẳng ở ngay bên dưới nhé!
Giải câu hỏi trang 80
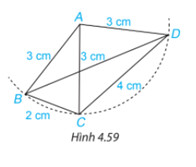
Tam giác cân là tam giác có hai cạnh bằng nhau. Hai cạnh bằng nhau đó gọi là 2 cạnh bên, cạnh còn lại của tam giác gọi là cạnh đáy.
+) Tam giác ABD cân tại đỉnh $A$ có:
$AB, AD$ là 2 cạnh bên
$BD$ là cạnh đáy
\widehat{B} , \widehat{D} là 2 góc ở đáy
\widehat{A} là góc ở đinh
+) Tam giác $ADC$ cân tại $A$ có:
$AC, AD$ là 2 cạnh bên
$DC$ là cạnh đáy
\widehat{C} , \widehat{D} là 2 góc ở đáy
\widehat{A} là góc ở đinh
+) Tam giác $ABC$ cân tại $A$ có:
$AB, AC$ là 2 cạnh bên
$BC$ là cạnh đáy
\widehat{C} , \widehat{B} là 2 góc ở đáy
\widehat{A} là góc ở đinh
Giải hoạt động 1 SGK trang 81
a) Chứng minh rằng \Delta $ABD$ = \Delta $ACD$ theo trường hợp cạnh – cạnh – cạnh.
b) Hai góc $B$ và $C$ của tam giác $ABC$ có bằng nhau không?
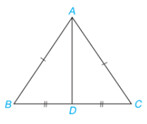
a) Chứng minh ba cạnh của 2 tam giác trên bằng nhau
b) Từ câu a) suy ra 2 cặp góc tương ứng bằng nhau.
a) Xét hai tam giác $ABD$ và $ACD$ có:
$AB = AC$
$AD$ chung
$BD=DC$
\Longrightarrow \Delta $ABD$ = \Delta $ACD$ (c.c.c)
b) Do \Delta $ABD$ = \Delta $ACD$ nên \widehat{B} = \widehat{C} ( 2 góc tương ứng)
Giải hoạt động 2 trang 81
Chứng minh rằng:
a) a) \widehat{MKP}= \widehat{NKP}
b) \Delta $MPK$ = \Delta $NPK$
c) Tam giác $MNP$ có cân tại $P$ không?
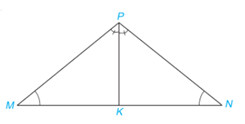
a) Sử dụng định lí: Tổng 3 góc trong một tam giác bằng 180 độ
b) Chứng minh 2 tam giác bằng nhau theo trường hợp góc – cạnh – góc
c) Sử dụng định nghĩa tam giác cân: Tam giác $MNP$ cân là tam giác có 2 cạnh bằng nhau
a) Xét tam giác $MPK$ có:
\widehat{PKM} + \widehat{MPK}+ \widehat{KMP}= $180^{\circ}$
Xét tam giá $NPK$ có:
\widehat{PKN} + \widehat{NPK}+ \widehat{KNP}= $180^{\circ}$
Mà $ \widehat{KMP}$ = $ \widehat{KNP}$; $ \widehat{MPK}$=$ \widehat{NPK}$
Suy ra $ \widehat{MKP}$ = $ \widehat{NKP}$
b) Xét hai tam giác $MPK$ và $NPK$ có:
$ \widehat{MPK}$ = $ \widehat{NPK}$
$PK$ chung
$ \widehat{MKP}$ = $ \widehat{NKP}$
\Longrightarrow \Delta $MPK$ = \Delta $NPK$ (c.g.c)
c) Do \Delta $MPK$ = \Delta $NPK$ nên $MP = NP$ (2 cạnh tương ứng)
\Longrightarrow Tam giác $MMNP$ cân tại $P$
Giải luyện tập 1 SGK trang 81
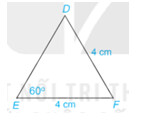
Chứng minh tam giác $DEF$ cân tại $F$ từ đó suy ra số đo các góc.
Cách 1: Vì tam giác $DEF$ có $DF=FE$ (=4cm) nên tam giác $DEF$ cân tại $F$.
Mà \widehat{E} = $60^{\circ}$
Do đó, \Delta $DEF$ đều. (Tam giác cân có 1 góc bằng $60^{\circ}$)
\Longrightarrow \widehat{D} = \widehat{F} = \widehat{E} = $60^{\circ}$
Cách 2: Xét tam giác $DEF$ có $DF=FE$ (=4cm) nên tam giác $DEF$ cân tại $F$.
Suy ra \Longrightarrow \widehat{D} = \widehat{E} = $60^{\circ}$ (Tính chất tam giác cân)
Áp dụng định lí tổng ba góc trong tam giác vào tam giác $DEF$, ta có:
\widehat{D} + \widehat{E} + \widehat{F} = $180^{\circ}$
\Longrightarrow $60^{\circ}$ + $60^{\circ}$ + $\widehat{F}$ = $180^{\circ}$
\Longrightarrow $\widehat{F}$ = $60^{\circ}$
Giải thử thách nhỏ SGK trang 81
a) Tam giác có ba góc bằng nhau?
b) Tam giác cân có một góc bằng $60^{\circ}$?
Áp dụng: Tam giác đều là tam giác có 3 cạnh bằng nhau hoặc ba góc bằng nhau.
a) Tam giác có ba góc bằng nhau là tam giác đều
b) Tam giác cân có 1 góc bằng 60 độ là tam giác đều.
Giải mục 2 SGK trang 81, 82, 83 Toán 7 Kết nối tri thức tập 1
Sau đây, hãy cùng HocThatGioi tìm ra đáp án chính xác nhất cho các câu hỏi và các hoạt động ở các trang 81, 82, 83 trong bài Tam giác cân. Đường trung trực của đoàn thẳng ở ngay bên dưới nhé!
Giải hoạt động 3 SGK trang 81
Gấp mảnh giấy lại như Hình 4.63 sao cho vị trí các điểm $A$ và $B$ trùng nhau. Mở mảnh giấy ra, kẻ một đường thẳng d theo nếp gấp.
a) Gọi $O$ là giao điểm của đường thẳng $d$ và $AB$. $O$ có là trung điểm của đoạn thẳng $AB$ không?
b) Dùng thước đo góc, kiểm tra đường thẳng $d$ có vuông góc với $AB$ không?
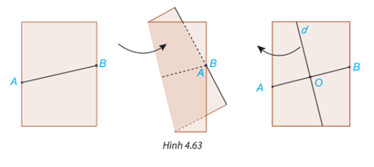
Dùng thước đo kiểm tra.
a) $O$ có là trung điểm của đoạn thẳng $AB$
b) Dùng thước đo góc ta thấy d có vuông góc với $AB$.
Giải câu hỏi SGK trang 82
Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.
Do: Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó
Nên hình a) Lan vẽ đúng.
Giải hoạt động 4 trang 82
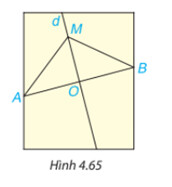
Dùng thước kiểm tra
Lấy điểm $M$ bất kì trên đường thẳng $d$ dùng thước kiểm tra ta thấy $AM$ bằng $BM$.
Giải luyện tập 2 SGK trang 83

Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Vì $M$ là một điểm nằm trên đường trung trực của đoạn thẳng $AB$ nên $MA=MB=3cm$.
\Longrightarrow \Delta $MAB$ cân tại $M$.
\Longrightarrow \widehat{MAB} = \widehat{MBA} = $60^{\circ}$
Giải bài tập trang 82 SGK Toán 7 tập 1 Kết nối tri thức
Bài học lý thuyết đã đi đến hồi kết, hãy cùng nhau giải các bài tập trong bài Tam giác cân. Đường trung trực của đoạn thẳng ở các trang 84 SGK Toán 7 Kết nối tri thức.
Giải bài 4.23 trang 84 SGK
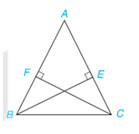
Chứng minh 2 tam giác bằng nhau để suy ra 2 cạnh tương ứng bằng nhau.
Do tam giác $ABC$ cân tại $A$ nên: \widehat{ABC} = \widehat{ACB} (tính chất tam giác cân)
Xét 2 tam giác vuông $BFC$ và $CEB$:
\widehat{ABC} = \widehat{ACB}
BC chung
\Longrightarrow \Delta $BFC$ = \Delta $CEB$ (cạnh huyền – góc nhọn)
\Longrightarrow $CF = BE$ (2 cạnh tương ứng)
Giải bài 4.24 trang 84 SGK
Chứng minh 2 tam giác $AMC$ và $AMB$ bằng nhau từ đó suy ra các cặp góc tương ứng bằng nhau.
$AM$ chung
$AB=AC$ (do tam giác $ABC$ cân tại $A$)
$MB=MC$ (gt)
\Longrightarrow \Delta $AMB$ = \Delta $AMC$ (c.c.c)
\Longrightarrow \widehat{BAM}= \widehat{CAM} (2 góc tương ứng)
Mà tia $AM$ nằm trong góc $BAC$
\Longrightarrow $AM$ là phân giác của góc $BAC$
Mặt khác: Do \Delta $AMB$ = \Delta $AMC$ nên \widehat{AMB} = \widehat{AMC} (2 góc tương ứng) mà \widehat{AMB} + \widehat{AMC} = $60^{\circ}$ (2 góc kề bù)
Nên \widehat{AMB} = \widehat{AMC} = $90^{\circ}$
Vậy nên $AM$ vuông góc với $BC$
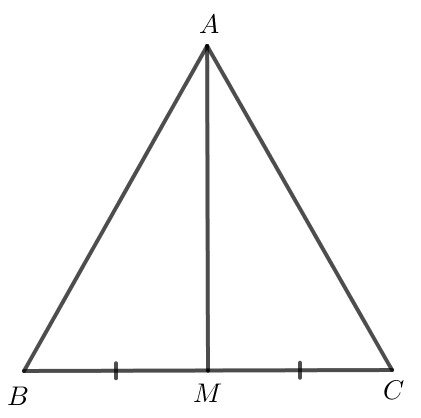
Giải bài 4.25 SGK trang 84
a) Giả sử $AM$ vuông góc với $BC$. Chứng minh rằng tam giác $ABC$ cân tại $A$.
b) Giả sử $AM$ là tia phân giác của góc $BAC$. Chứng minh rằng tam giác $ABC$ cân tại $A$.
a) Chứng minh tam giác hai tam giác $AMB$ và $AMC$ bằng nhau
\Longrightarrow Tam giác $ABC$ cân.
b) Từ $M$ kẻ hai đường vuông góc với $AC$ và $AB$ từ đó chứng minh hai góc $B$ và $C$ bằng nhau.
\Longrightarrow Chứng minh hai tam giác $AMB$ và $AMC$ bằng nhau
\Longrightarrow Tam giác $ABC$ cân
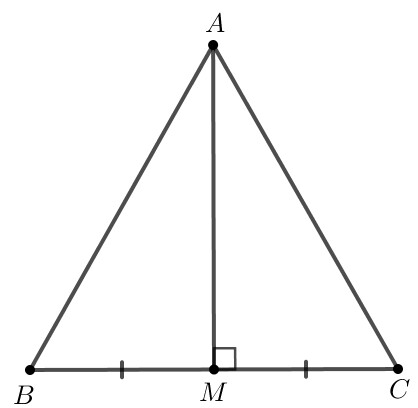
a)
$AM$ chung
$BM=CM$ (gt)
$\Longrightarrow \Delta$ $AMC$ = $\Delta$ $AMB$(hai cạnh góc vuông)
$ \Longrightarrow$ $AC$ = $AB$ (2 cạnh tương ứng)
\Longrightarrow Tam giác $ABC$ cân tại $A$
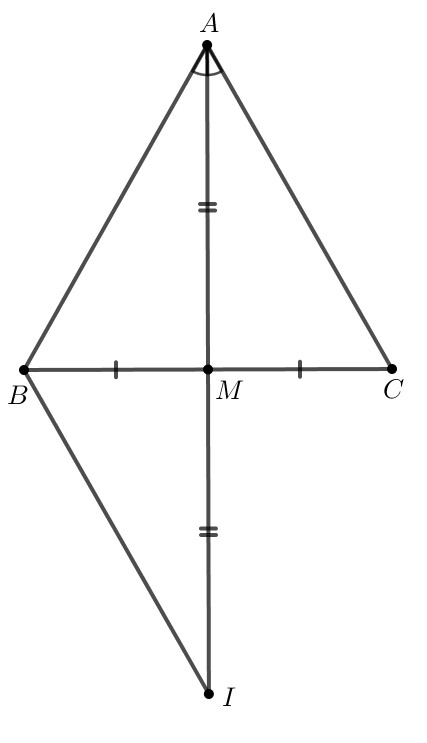
b)
$MG$ vuông góc với $AC$ ($G$ thuộc $AC$)
Xét 2 tam giác vuông $AHM$ và $AGM$ có:
$AM$ chung
\widehat{HAM} = \widehat{GAM} (do $AM$ là tia phân giác của góc $BAC$)
$ \Longrightarrow $ $ \Delta$ $AHM$ = $\Delta$ $AGM$ (cạnh huyền – góc nhọn)
$\Longrightarrow$ $HM$ = $GM$ (2 cạnh tương ứng)
Xét 2 tam giác vuông $BHM$ và $CGM$ có:
$BM=CM$ (giả thiết)
$MH=MG$ (chứng minh trên)
$ \Longrightarrow \Delta$ $BHM$ = $\Delta$ $CGM$[ (cạnh huyền – cạnh góc vuông)
\Longrightarrow \widehat{HBM} = \widehat{GCM} (2 góc tương ứng)
$\Longrightarrow $ Tam giác $ABC$ cân tại $A$
Giải bài 4.26 SGK trang 84
Hãy giải thích các khẳng định sau:
a) Tam giác vuông cân thì cân tại đỉnh góc vuông;
b) Tam giác vuông cân có hai góc nhọn bằng $45^{\circ}$
c) Tam giác vuông có một góc nhọn bằng $45^{\circ}$ là tam giác vuông cân.
Áp dụng tổng ba góc trong tam giác bằng 180 độ.
a) Do tổng ba góc trong 1 tam giác bằng 180 độ nên tam giác không thể có 2 góc vuông
\Longrightarrow Tam giác vuông cân sẽ có 2 góc nhọn bằng nhau
\Longrightarrow Tam giác vuông cân thì cân tại đỉnh góc vuông.
b) Giả sử hai góc nhọn trong tam giác vuông là x, ta có:
$x + x$ + $90^{\circ}$ = $180^{\circ}$
\Longrightarrow $2x$ = $90^{\circ}$
\Longrightarrow $x$ = $45^{\circ}$
Vậy tam giác vuông cân có hai góc nhọn bằng $45^{\circ}$
c) Gọi góc còn lại của tam giác vuông có 1 góc nhọn bằng $45^{\circ}$ là x, ta có:
$x$ + $45^{\circ}$ + $90^{\circ}$ = $180^{\circ}$ \Longrightarrow $ x$ = $45^{\circ}$
Vậy tam giác vuông có một góc nhọn bằng $45^{\circ}$ là tam giác vuông cân.
Giải bài 4.27 SGK trang 84
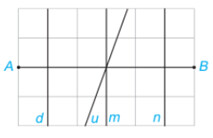
Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.
Quan sát hình 4.70 ta thấy đường thẳng $m$ vuông góc với đoạn thẳng $AB$ tại trung điểm của $AB$ nên $m$ là đường trung trực của $AB$.
Giải bài 4.28 SGK trang 84
Chứng minh 2 tam giác bằng nhau suy ra 2 cạnh tương ứng bằng nhau, 2 góc tương ứng bằng nhau
Chú ý: Hai góc kề bù bằng nhau thì mỗi góc bằng 90 độ
Xét 2 tam giác vuông $ADC$ và $ADB$ có:
$AD$ chung
$AC=AB$ (cmt)
\Longrightarrow \Delta $ADC$ = \Delta $ADB$ (cạnh huyền – góc vuông)
\Longrightarrow $CD = BD$ (2 cạnh tương ứng)
\Longrightarrow $D$ là trung điểm của $BC$
Mà $AD$ \bot $BC$ tại $D$
Vậy $AD$ là đường trung trực của đoạn thẳng $BC$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Bà viết này đã giải quyết tất cả các bài tập, câu hỏi, các hoạt động của bài 16 Tam giác cân. Đường trung trực của đoạn thẳng thuộc chương 3 trang 81, 82, 83, 84 Toán 7 Kết nối tri thức Tập 1. Hy vọng, qua bài viết này bạn có thể nắm rõ tất cả các kiến thức và áp dụng nó vào thực tế một cách tốt nhất. Chúc các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





