Giải SGK bài 35 chương 9 trang 77, 78, 79, 80, 81 Toán 7 Kết nối tri thức Tập 2
Ở bài viết này, HocThatGioi sẽ cùng bạn giải quyết tất cả những câu hỏi khởi động, vận dụng, bài tập trong bài Sự đồng quỵ của ba đường trung trực, ba đường cao trong một tam giác. Các bài tập sau đây thuộc bài 35 chương 9 – Tỉ lệ thức và đại lượng tỉ lệ trang 77, 78, 79, 80, 81 Toán 7 Kết Nối Tri Thức Tập 2. Hy vọng, sau bài viết này các bạn có thể nắm vững tất cả các kiến thức đã học, và có thể áp dụng chúng để giải tất cả bài tập một cách dễ dàng theo những lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Giải SGK mục 1 trang 77, 78, 79 Toán 7 Kết nối tri thức Tập 2
Dưới đây là phương pháp cụ thể và bài giải chi tiết, dễ hiểu cho các câu hỏi hoạt động, thực hành cùng phần luyện tập ở các trang 77, 78, 79 SGK Toán 7 Kết nối tri thức Tập 2. Cùng HocThatGioi đi tìm đáp án và phương pháp giải hay nhất ngay nhé!
Giải câu hỏi SGK trang 77
Đường trung trực của đoạn thẳng là đường vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.
Mỗi tam giác có $3$ đường trung trực.
Giải SGK hoạt động 1 trang 78
Đường trung trực của đoạn thẳng là đường vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.
Giải SGK hoạt động 2 trang 78
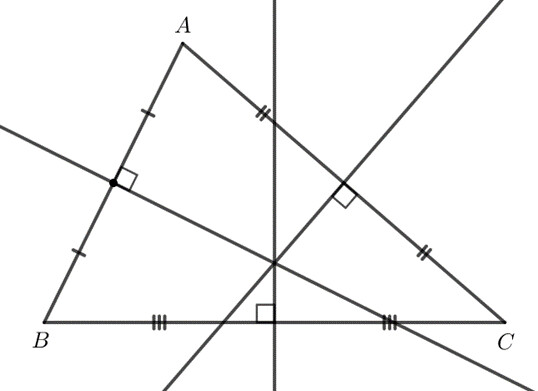
Cho $O$ là giao điểm các đường trung trực của hai cạnh $BC$ và $CA$ (H.9.38)
a) Tại sao $OB = OC, OC = OA$.
b) Điểm $O$ có nằm trên đường trung trực của $AB$ không?
Gọi $M$ là trung điểm $BC$, $N$ là trung điểm $AC$
a) Chứng minh $\Delta OBM = \Delta OCM$ ($c – g – c$), $\Delta OAN = \Delta OCN$($c – g – c$)
b) Điểm cách đều hai đầu mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đấy.
a)
Gọi $M$ là trung điểm của $BC, N$ là trung điểm $AC$.
Xét $\Delta OBM$ và $ \Delta OCM$ có:
$BM = CM$ (gt)
$\widehat{OMB} = \widehat{OMC} = 90^{\circ}$
$OM$ chung
$\Rightarrow \Delta OBM= \Delta OCM$ ($c−g−c$)
$\Rightarrow OB=OC$ (cạnh tương ứng)
Chứng minh tương tự: $\Delta OAN= \Delta OCN$ ($c – g – c$) $ \Rightarrow OA=OC$ (cạnh tương ứng)
b) Ta có: $\Longrightarrow \begin{cases} OA = OC \\ OB = OC \end{cases}$ (cmt) $\Longrightarrow OA = OB$
$ \Longrightarrow O$ cách đều hai đầu mút của đoạn thẳng $AB$
$\Longrightarrow O$ nằm trên đường trung trực của đoạn thẳng $AB$ (tính chất đường trung trực của đoạn thẳng)
Giải SGK luyện tập 1 trang 79
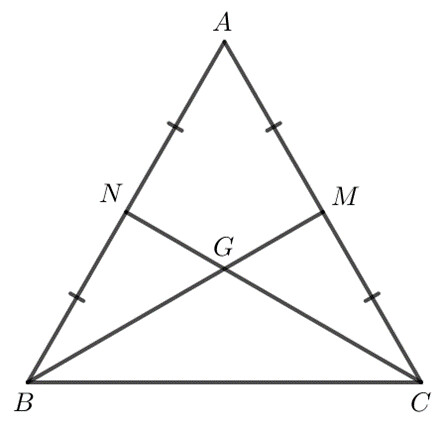
Do $\Delta ABC$ đều nên $AB = BC = CA$ và $\widehat{ABC} = \widehat{ACB} = \widehat{BAC}$.
$M$ là trung điểm của $AC$ nên $AM = MC$.
Xét $\Delta ABM$ và $\Delta CBM$ có:
$AB = CB$ (chứng minh trên).
$\widehat{BAM} = \widehat{BCM}$ (chứng minh trên).
$AM = CM$ (chứng minh trên).
Suy ra $\Delta ABM = \Delta CBM$ ($c – g – c$).
Do đó $\widehat{BMA} = \widehat{BMC}$ ($2$ góc tương ứng).
Mà $\widehat{BMA} + \widehat{BMC} = 180 ^{\circ}$ nên $\widehat{BMA} = \widehat{BMC} = 90^{\circ}$.
Do đó $BM \perp AC$.
$BM$ vuông góc với $AC$ tại trung điểm $M$ của $AC$ nên $BM$ là đường trung trực của $AC$.
$N$ là trung điểm của $AB$ nên $AN = BN$.
Xét $\Delta CAN$ và $\Delta CBN$ có:
$CA = CB$ (chứng minh trên).
$\widehat{CAN} = \widehat{CBN}$ (chứng minh trên).
$AN = BN$ (chứng minh trên).
Suy ra $\Delta CAN = \Delta CBN$ ($c – g – c$).
Do đó $\widehat{CNA} = \widehat{CNB}$($2$ góc tương ứng).
Mà $\widehat{CNA} + \widehat{CNB} = 180 ^{\circ}$ nên $\widehat{CNA} = \widehat{CNB} = 90^{\circ}$.
Do đó $CN \perp AB$.
$CN$ vuông góc với $AB$ tại trung điểm $N$ của $AB$ nên $CN$ là đường trung trực của $AB$.
$G$ là giao điểm $2$ đường trung trực của $\Delta ABC$ nên $G$ cách đều $3$ đỉnh của tam giác.
Giải SGK vận dụng 1 trang 79
Địa điểm khoan giếng cách đều $3$ ngôi nhà.
$3$ ngôi nhà không thẳng hàng nên tạo thành $1$ tam giác, ta gọi là tam giác $ABC$.
Điểm khoan giếng cách đều $3$ ngôi nhà khi và chỉ khi điểm khoan giếng là giao điểm của $3$ đường trung trực của tam giác $ABC$.
Vậy, ta cần vẽ $2$ đường trung trực của tam giác $ABC$, chúng cắt nhau tại đâu thì đó là điểm cần khoan giếng.
Giải SGK thử thách nhỏ trang 79
Điểm cách đều $2$ mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng.
$Q$ cách đều $3$ đỉnh của tam giác $ABC$ nên $QA = QB = QC$.
Do $QA = QB$ nên $Q$ nằm trên đường trung trực của $AB$.
Do $QB = QC$ nên $Q$ nằm trên đường trung trực của $BC$.
Do $QC = QA$ nên $Q$ nằm trên đường trung trực của $CA$.
Do đó $Q$ là giao điểm ba đường trung trực của tam giác $ABC$.
Giải SGK mục 2 trang 79, 80, 81 Toán 7 Kết nối tri thức Tập 2
Sau đây, hãy cùng HocThatGioi tìm ra đáp án chính xác nhất cho các hoạt động và các câu hỏi luyện tập ở các trang 79, 80, 81 trong bài Sự đồng quỵ của ba đường trung trực, ba đường cao trong một tam giác ở ngay bên dưới nhé!
Giải SGK câu hỏi trang 79
Đường cao là đoạn thẳng đi qua đỉnh và vuông góc với cạnh đối diện.
Ứng với $1$ cạnh của tam giác, ta có $1$ đường cao
Vậy mỗi tam giác có $3$ đường cao.
Giải SGK hoạt động 3 trang 79
Đường cao của một tam giác là đoạn thẳng kẻ từ một đỉnh và vuông góc với cạnh đối diện
Giải SGK luyện tập 2 trang 81
b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
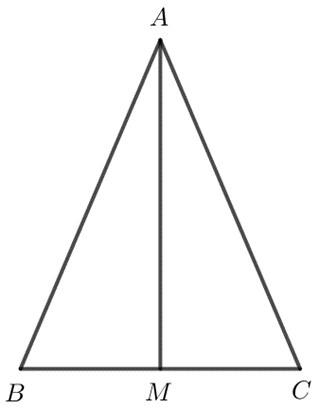
Do tam giác $ABC$ cân tại $A$ nên $AB = AC$ và $\widehat{ABM} = \widehat{ACM}$.
Do $AB = AC$ nên $A$ nằm trên đường trung trực của $BC$.
Do đó $AM \perp BC$ nên $AM$ là đường cao của tam giác $ABC$.
Xét $\Delta ABM$ có $\widehat{ABM} + \widehat{MAB}$ = $90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).
Suy ra $\widehat{MAB} =90^{\circ} − \widehat{ABM}$ ($1$).
Xét $\Delta ACM$ có $\widehat{ACM} + \widehat{MAC}= 90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).
Suy ra $\widehat{MAC} =90^{\circ} − \widehat{ACM}$ ($2$).
Mà $\widehat{ABM} = \widehat{ACM}$ nên từ ($1$) và ($2$) ta có $\widehat{MAB} = \widehat{MAC}$.
Do đó $AM$ là tia phân giác của $\widehat{BAC}$
Vậy đường trung trực của cạnh $BC$ là đường cao và cũng là đường phân giác xuất phát từ đỉnh $A$ của tam giác $ABC$.
Gọi $M, N, P$ lần lượt là trung điểm của $AB, AC, BC$.
Do $O$ cách đều $3$ đỉnh của tam giác $ABC$ nên $O$ là giao điểm $3$ đường trung trực của tam giác $ABC$.
Do đó $OM \perp AM, ON \perp AN, OP \perp CP$.
$\Delta ABC$ đều nên $AB = AC = BC$.
Do $M, N, P$ lần lượt là trung điểm của $AB, AC, BC$ nên $AM = AN = NC = CP$.
Xét $\Delta OAM$ vuông tại $M$ và $\Delta OAN$ vuông tại $N$:
$AM = AN$ (chứng minh trên).
$OA$ chung.
Suy ra $\Delta OAM = \Delta OAN$ (cạnh huyền – cạnh góc vuông).
Do đó $OM = ON$ ($2$ cạnh tương ứng) ($2$).
Xét $\Delta OCN$ vuông tại $N$ và $\Delta OCP$ vuông tại $P$:
$CN = CP$ (chứng minh trên).
$OC$ chung.
Suy ra $\Delta OCN$ = $\Delta OCP$ (cạnh huyền – cạnh góc vuông).
Do đó $ON = OP$ ($2$ cạnh tương ứng) ($2$).
Từ ($1$) và ($2$) suy ra $OM = ON = OP$.
Vậy trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
Giải SGK bài tập trang 81 Toán 7 Kết nối tri thức Tập 2
Hãy cùng HocThatGioi áp dụng các lý thuyết, công thức, định lý,… đã học để giải các bài tập trong bài 35 Sự đồng quỵ của ba đường trung trực, ba đường cao trong một tam giác ở trang 81 SGK Toán 7 Kết nối tri thức tập 2.
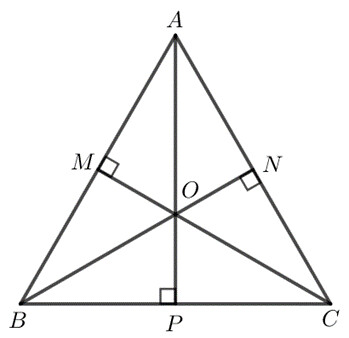
Giải SGK bài 9.26 trang 81
-Trực tâm của tam giác là giao điểm của ba đường cao.
-Xác định các đường cao của mỗi tam giác.
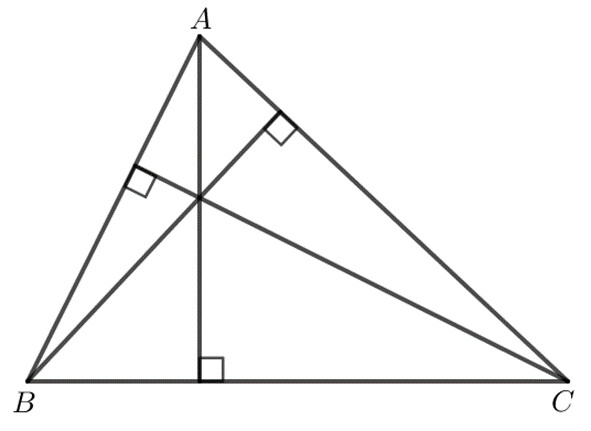
Xét $\Delta HBC$ có $HD \perp BC, BF \perp HC$.
$HD$ cắt $BF$ tại $A$ nên $A$ là trực tâm của $\Delta HCA$.
Xét $\Delta HCA$ có $HE \perp AC, BF \perp HC$.
$HE$ cắt $BF$ tại $B$ nên $B$ là trực tâm của $\Delta HCA$.
Xét $\Delta HAB$ có $HF \perp AB, AE \perp HB$.
$HF$ cắt $AE$ tại $C$ nên $C$ là trực tâm của $\Delta HAB$.
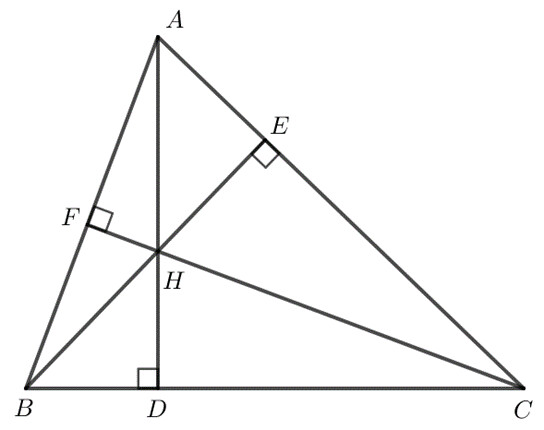
Giải SGK bài 9.27 trang 81
Ta có $\widehat{BAD} = \widehat{EAH}$ ($2$ góc đối đỉnh), $\widehat{DAC} = \widehat{FAH}$ ($2$ góc đối đỉnh).
Do đó $\widehat{BAD} + \widehat{DAC} = \widehat{EAH} + \widehat{FAH} = 100^{\circ}$.
Xét $\Delta FAH$ vuông tại $F$: $\widehat{FHA} + \widehat{FAH} = 90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).
Do đó $\widehat{FHA} =90^{\circ}− \widehat{FAH}$
Xét $\Delta EAH$ vuông tại $E$: $\widehat{EHA} + \widehat{EAH} = 90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).
Do đó $\widehat{EHA} = 90^{\circ} − \widehat{EAH}$
Khi đó $\widehat{FHA} + \widehat{EHA} = 90^{\circ}− \widehat{FAH} + 90^{\circ}− \widehat{EAH}$
hay $\widehat{BHC} = 180^{\circ} − (\widehat{FAH} + \widehat{EAH})$.
Do đó $\widehat{BHC} = 180^{\circ} – 100^{\circ} = 80^{\circ}$.
Vậy $\widehat{BHC} = 80^{\circ}$.
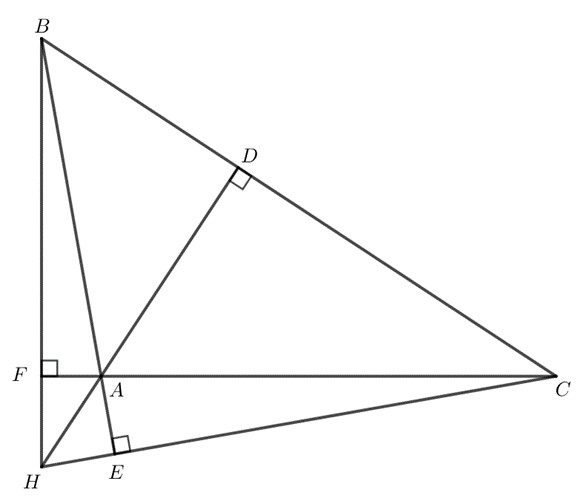
Giải SGK bài 9.28 trang 81
Do $OA = OB$ nên $\Delta OAB$ cân tại $O$.
Do đó $\widehat{OAB} = \widehat{OBA}$.
Do $OA = OC$ nên $\Delta OAC$ cân tại $O$.
Do đó $\widehat{OAC}= \widehat{OCA}$
Khi đó $\widehat{OAB} + \widehat{OAC} = \widehat{OBA} + \widehat{OCA}$ hay $\widehat{BAC} = \widehat{ABC} + \widehat{ACB}$.
Xét $\Delta ABC$ có $\widehat{BAC} + \widehat{ABC} + \widehat{ACB} = 180^{\circ}$.
Mà $\widehat{BAC} = \widehat{ABC} + \widehat{ACB}$ nên $2\widehat{BAC}=180^{\circ}$ hay $\widehat{BAC} = 90^{\circ}$.
Do đó $\Delta ABC$ vuông tại $A$.
Vậy nếu $O$ nằm trên một cạnh của tam giác $ABC$ và $O$ cách đều ba đỉnh của tam giác $ABC$ thì $ABC$ là một tam giác vuông.
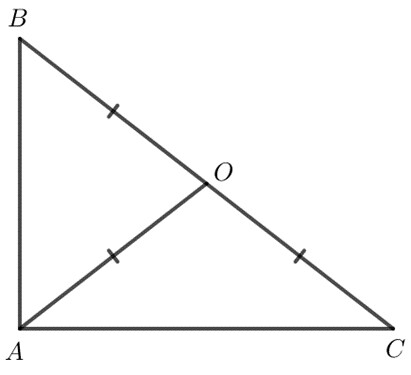
Giải SGK bài 9.29 trang 81
b) Trên bản đồ, ba khu dân cư được quy hoạch tại điểm $A, B, C$ không thẳng hàng. Hãy tìm trên bản đồ một điểm $M$ cách đều $A, B, C$ để quy hoạch một trường học

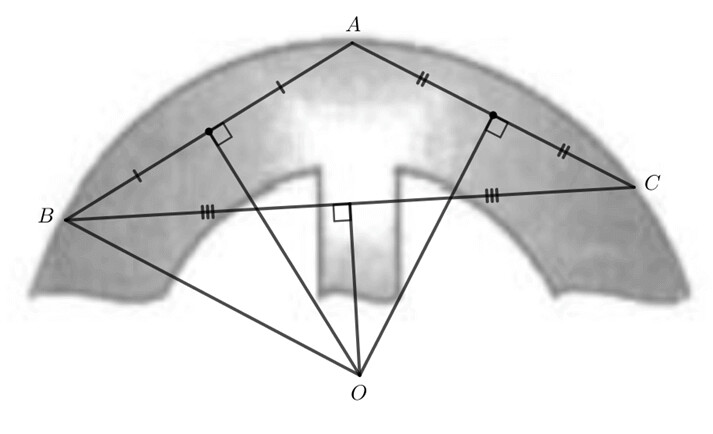
Bước $1$. Xác định $3$ điểm $A, B, C$ nằm trên đường viền của chi tiết máy.
Bước $2$. Xác định các đường trung trực của tam giác $ABC$.
Bước $3$. Xác định giao điểm $O$ của ba đường trung trực của tam giác $ABC$.
Bước $4$. Độ dài đoạn thẳng $OB$ là bán kính của đường tròn.

Do $M$ cách đều $A$ và $B$ nên $MA = MB$.
Do đó $M$ nằm trên đường trung trực của $AB$.
Do $M$ cách đều $B$ và $C$ nên $MB = MC$.
Do đó $M$ nằm trên đường trung trực của $BC$.
Vậy $M$ là giao điểm $3$ đường trung trực của tam giác $ABC$.
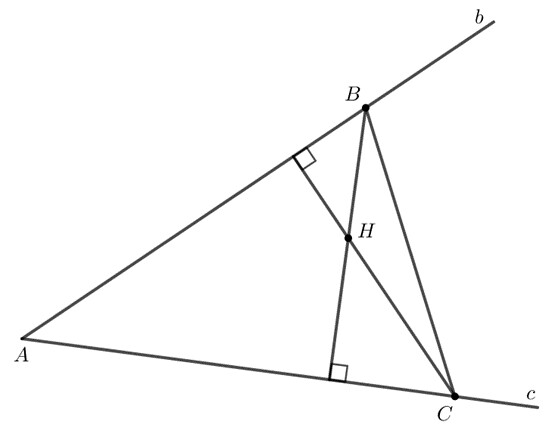
Giải SGK bài 9.30 trang 81
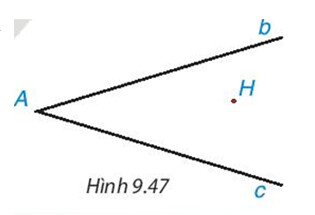
Để vẽ trực tâm ta xác định $2$ đường cao của tam giác trên. Giao điểm của $2$ đường cao chính là trực tâm của tam giác.
Ta thực hiện theo các bước như sau:
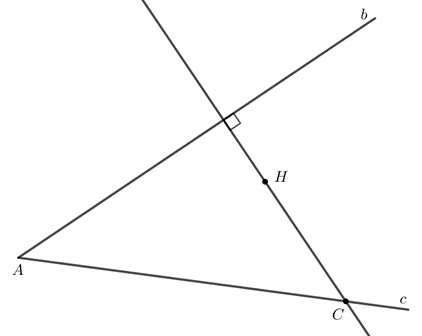
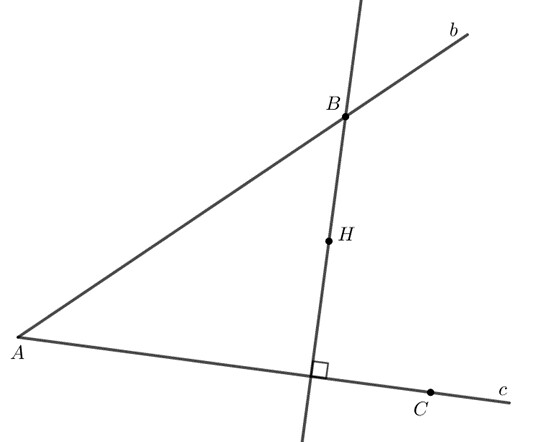
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Bà viết này đã giải quyết tất cả các bài tập, câu hỏi, các hoạt động của bài Sự đồng quỵ của ba đường trung trực, ba đường cao trong một tam giác. Các bài tập sau đây thuộc Giải SGK Bài 35 chương 9 trang 77, 78, 79, 80, 81 Toán 7 Kết nối tri thức Tập 2. Hy vọng, qua bài viết này bạn có thể nắm rõ tất cả các kiến thức và giải tất cả các bài tập một cách tốt nhất. Chúc các bạn có một buổi học thật thú vị nhé!





