Cách giải và bài tập minh họa về dạng toán liên quan đến sửa tật ở mắt hay nhất
Bài viết dưới đây, HocThatGioi sẽ trình bày cho các bạn về cách giải và kèm theo một số bài tập ví dụ minh họa có đáp án chi tiết liên quan đến sửa tật ở mắt để các bạn cùng tham khảo nhé. Các bạn có thể xem thêm phần lý thuyết liên quan về mắt tại bài Lý thuyết về Mắt và các dụng cụ quang học nhé!
1. Cách giải bài toán liên quan đến sửa tật của mắt
Qua phần lý thuyết về mắt thì chúng ta cũng đã thấy mắt của chúng ta thường có 3 tật sau: Tật cận thị, viễn thị và lão thị. Vì vậy hôm nay chúng ta sẽ giải quyết về vấn đề khắc phục tật ở mắt qua các bài toán nhé.
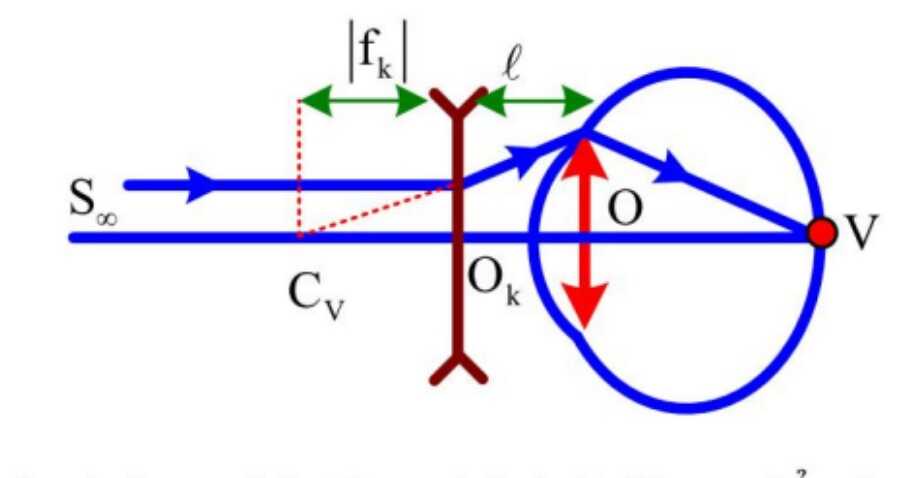
1.1 Sửa tật cận thị
- Đeo kính phân kì để nhìn rõ các vật ở vô cực mà mắt không phải điều tiết (vật ở vô cùng qua O_k cho ảnh ảo nằm tại điểm cực viễn)
- Công thức liên quan:
1.2 Sửa tật viễn thị và lão thị
- Đeo kính hội tụ để nhìn rõ các vật ở gần nhất và cách mắt 25 cm mà mắt phải điều tiết tối đa (vật ở cách mắt qua O_k cho ảnh ảo nằm tại điểm C_C)
- Công thức liên quan
\rightarrow f_k=\frac{d.d’}{d+d’}
2. Bài tập minh họa về sửa tật ở mắt
Dưới đây, sẽ là một vài ví dụ được HocThatGioi tổng hợp và kèm lời giải chi tiết để các bạn có thể hiểu hơn về dạng toán sửa tật ở mắt nhé!
Người đó đeo kính phân kì để nhìn rõ các vật ở vô cực mà mắt không phải điều tiết (vật ở vô cùng qua O_K cho ảnh ảo nằm tại điểm cực viễn C_V)
\left | f_K \right |+ l= OC_V
\rightarrow f_K= -0,8 (m)
D_K=\frac{1}{f_K}=-1,25 (dp)
Người đó đeo kính phân kì để nhìn rõ các vật ở vô cực mà mắt không phải điều tiết (vật ở vô cùng qua O_Kcho ảnh ảo nằm tại điểm cực viễn C_V)
Áp dụng công thức sau:
\left | f_K \right |+ l= OC_V (1)
Ta có: OC_V= OC_C+ C_CC_V
\rightarrow OC_V=0,125 + 0,375=0,5 (m) (2)
Thay (2) vào (1)
\Rightarrow f_K= -0,5 (m)\rightarrow D_K=\frac{1}{f_K}=-2 (dp)
Để khi đeo kính nhìn được vật gần nhất cách mắt 25 cm thì qua kính cho một ảnh ảo tại điểm cực cận của mắt
Áp dụng công thức tính tiêu cự:
f=\frac{d.d’}{d+ d’}=\frac{25.(-50)}{25-50}=50 (cm)= 0,5 (m)
Độ tụ của kính:
D=\frac{1}{f}=\frac{1}{0,5}=2 (dp)
Người ngày nhìn được vật ở xa mà không phải điều tiết nên OC_V=\infty .
Để khi đeo kính nhìn được vật gần nhất cách mắt 25 cm thì qua kính cho một ảnh ảo tại điểm cực cận của mắt:
d=0,25-l=0,25 (m)) (1) (1)
d’=-(OC_C-l)= -OC_C (2)
Mà ta có:
D=\frac{1}{f}=\frac{1}{d}+\frac{1}{d’} (3)
Từ (1), (2) và (3) ta có:
D=\frac{1}{d}+\frac{1}{d’}
1=\frac{1}{0,25}+\frac{1}{-OC_C}
\rightarrow OC_C= \frac{1}{3}
Độ biến thiên độ tụ của mắt:
\Delta D=D_{max}-D_{min}=\frac{1}{OC_C}-\frac{1}{OC_V}= 3 (dp) (vì OV bằng vô cùng)
Độ biến thiên độ tụ của mắt là:
D_{max}- D_{min}=1
\Leftrightarrow \frac{1}{OC_C}-\frac{1}{OC_V}=1
\rightarrow OC_C= 1 (m)
Khi đeo kính để nhìn vật cách mắt 25 cm mà mắt điều tiết tối đa thì ảnh A_1B_1 nằm tại điểm cực cận của mắt.
d’=l- OC_V=-0,98 (m) (1)
d=0,25-0,02=0,23 (m) (2)
Từ (1) và (2) ta có:
D_K=\frac{1}{d}+\frac{1}{d’}=\frac{1}{0,23}+\frac{1}{-0,98}= 3,33 (dp)
Như vậy, bài viết về Cách giải và bài tập liên quan đến sửa tật ở mắt của HocThatGioi đến đây đã hết. Qua bài viết, hi vọng sẽ giúp các bạn biết thêm về các giải các bài toán liên quan đến sửa tật ở mắt. Đừng quên Like và Share để HocThatGioi ngày càng phát triển. Cảm ơn các bạn đã theo dõi hết bài viết và chúc các bạn học thật tốt!