Giải SGK Bài 14 Chương 4 Trang 70, 71, 72, 73, 74 Toán 7 Kết Nối Tri Thức
Ở bài viết này, HocThatGioi sẽ cùng bạn giải quyết tất cả những câu hỏi khởi động, vận dụng, bài tập trong bài Trường hợp bằng nhau thứ hai và thứ ba của tam giác. Các bài tập sau đây thuộc bài 14 chương 4 – Trường hợp bằng nhau thứ hai và thứ ba của tam giác trang 70, 71, 72, 73, 74 Toán 7 Kết Nối Tri Thức. Hy vọng, sau bài viết này các bạn có thể nắm rõ những kiến thức đã học và có thể áp dụng chúng một cách dễ dàng theo những lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi sách giáo khoa trang 70, 71, 71,73 SGK Bài 14 Chương 4 Kết Nối Tri Thức
Dưới đây là phương pháp cụ thể và bài giải chi tiết, dễ hiểu cho các câu hỏi hoạt động, thực hành cùng phần luyện tập ở các trang 70, 71, 72, 73 trong bài Trường hợp bằng nhau thứ hai và thứ ba của tam giác. Cùng HocThatGioi đi tìm đáp án và phương pháp giải hay nhất ngay nhé!
Hoạt động 1: Trang 70 SGK Toán 7 Kết nối tri thức
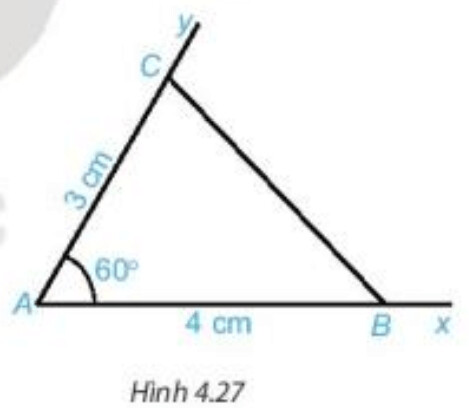
Dùng thước thẳng có vạch chia đo độ dài cạnh $BC$ của tam giác ABC .
Dùng thước thẳng có vạch chia đo độ dài cạnh $BC$ ta được: $BC$=3,6cm.
Hoạt động 2: Trang 70 SGK Toán 7 Kết nối tri thức
Dùng thước thẳng có vạch chia hoặc compa để so sánh độ dài các cạnh tương ứng của hai tam giác $ABC$ và $ABC$.
– Hai tam giác ABC và ABC có bằng nhau không?
– Độ dài các cạnh $AB$ và $AB$ của hai tam giác em vừa vẽ có bằng các cạnh $AB$ và $AB$ của hai tam giác các bạn khác về không?
– Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ không?
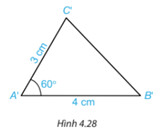
Dùng thước thẳng có vạch chia đo độ dài cạnh $BC$ của tam giác ABC.
– Độ dài các cạnh tương ứng của 2 tam giác ABC và A’B’C’ bằng nhau.
– Hai tam giác ABC và A’B’C’ có bằng nhau.
– Độ dài các cạnh $AB’$ và $AC’$ của hai tam giác em vừa vẽ có bằng các cạnh $AB’$ và $AC’$ của hai tam giác các bạn khác vẽ.
– Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ.
Câu hỏi 1 trang 71 SGK Toán 7 Kết nối tri thức

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau (c.g.c).
Xét 2 tam giác ABC và MNP có:
$AB=MN$ (gt)
\widehat{BAC} = \widehat{NMP}
$AC=MP$ (gt)
Vậy \bigtriangleup ABC = \bigtriangleup MNP (c.g.c)
Luyện tập 1 Trang 71 SGK Toán 7 Kết nối tri thức
Hai tam giác ABC và MNP trong Hình 431 có bằng nhau không? Vì sao?
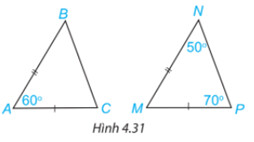
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau (c.g.c).
Xét tam giác MNP có:
\widehat{M} + \widehat{N} + \widehat{P} =180^{\circ}
\Longrightarrow \widehat{M} + 50^{\circ} + 70^{\circ} = 180^{\circ}
\Longrightarrow \widehat{M} = 60^{\circ}
Xét 2 tam giác ABC và MNP có:
$AB=MN$ (gt)
\widehat{BAC} = \widehat{NMP} = (60^{\circ} )
$AC=MP$ (gt)
Vậy \bigtriangleup BAC = \bigtriangleup NMP (c.g.c)
Câu hỏi vận dụng Trang 71 SGK Toán 7 Kết nối tri thức
Cho Hình 4.32, biết \widehat{OAB} = \widehat{ODC} , $OA=OD$ và $AB=CD$.
Chứng minh rằng:
a, $AC=DB$.
b, \bigtriangleup OAC = \bigtriangleup ODB.
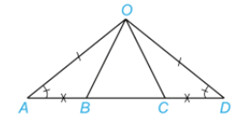
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau (c.g.c).
a) Ta có:
$AB = CD$
\Longrightarrow $AB$ + $BC$ = $CD$ + $BC$
\Longrightarrow $AC = BD$
b) Xét tam giác OAC và ODB có:
$AC = BD$ (cmt)
\widehat{A} = \widehat{D} (gt)
$OA = OD$ (gt)
\Longrightarrow \bigtriangleup OAC = \bigtriangleup ODB (c.g.c)
Hoạt động 3 Trang 72 SGK Toán 7 Kết nối tri thức
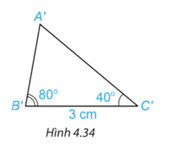
Vẽ đoạn thẳng $BC=3cm$. Vẽ hai tia $Bx$ và $Cy$ sao cho
\widehat{xBC} = 80^{\circ} , \widehat{yCB} = 40^{\circ} như Hình 4.33.
Lấy giao điểm $A$ của hai tia $Bx$ và $Cy$, ta được tam giác $ABC$ (H.4.33).
Dùng thước thẳng có vạch chia độ dài hai cạnh $AB$, $AC$ của tam giác ABC.

Dùng thước thẳng có vạch chia độ dài hai cạnh $AB$, $AC$ của tam giác ABC.
$AB=2,2 cm$
$AC=3,4 cm$
Hoạt động 4 Trang 72 SGK Toán 7 Kết nối tri thức
Dùng thước thẳng có vạch chia hoặc compa so sánh độ dài các cạnh của hai tam giác ABC và A’B’C’
Hai tam giác ABC và A’B’C’ có bằng nhau không?
Dùng thước thẳng hoặc compa để đo độ dài các cạnh của 2 tam giác và so sánh
$A’B’=2,2 cm$
$A’C’=3,4 cm$
Hai tam giác ABC và A’B’C’ có bằng nhau.
Câu hỏi Trang 72 SGK Toán 7 Kết nối tri thức
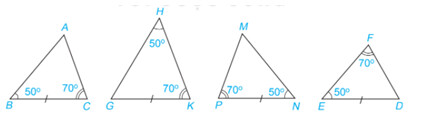
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau
Cặp tam giác bằng nhau là:
\bigtriangleup ABC = \bigtriangleup MNP vì
\widehat{B} = \widehat{N} = ( 50^{\circ} )
$BC=NP$
\widehat{C} = \widehat{P} = ( 70^{\circ} )
Vậy \bigtriangleup ABC = \bigtriangleup MNP (c.g.c)
Câu hỏi luyện tập 2 Trang 73 SGK Toán 7 Tập 1 Kết nối tri thức
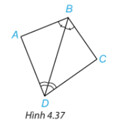
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau (g.c.g).
Xét hai tam giác ABD và CBD có:
\widehat{ABD} = \widehat{CBD}
$BD$ Chung
\widehat{ADB} = \widehat{CDB}
Vậy \bigtriangleup ABD = \bigtriangleup CBD (c.g.c)
Thử thách nhỏ Trang 73 SGK Toán 7 tập 1 Kết nối tri thức
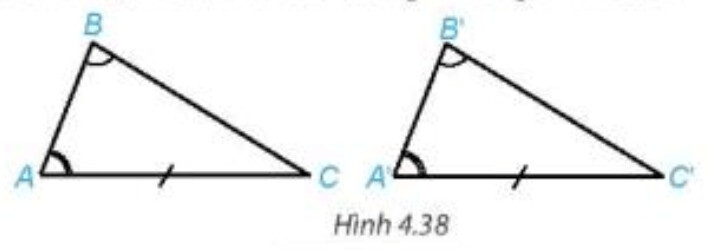
Kiểm tra xem cặp góc còn lại của hai tam giác có bằng nhau không rồi sử áp dụng trường hợp bằng nhau thứ ba của tam giác.
Do hai tam giác trên có hai cặp góc bằng nhau nên cặp góc còn lại bằng nhau.
Xét \bigtriangleup ABC và \bigtriangleup A’B’C’ có
\widehat{A} = \widehat{A’} (gt)
$AC = A’C’$ (gt)
\widehat{C} = \widehat{C’} (cmt)
\Longrightarrow \bigtriangleup ABC = \bigtriangleup A’B’C’ (g.c.g)
Vậy hai tam giác đã cho bằng nhau theo trường hợp góc – cạnh – góc.
Bài tập 4.12 Trang 73 SGK Toán 7 tập 1 Kết nối tri thức
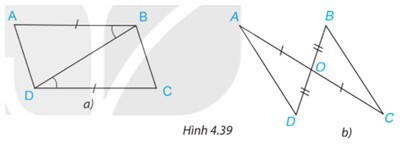
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
a, Xét \bigtriangleup ABD và \bigtriangleup CDB có:
$AB=CD$ (gt)
\widehat{ABD} = \widehat{CDB} (gt)
$BD$ chung
\bigtriangleup ABD= \bigtriangleup CDB (c.g.c)
b, Xét \bigtriangleup OAD và \bigtriangleup OCB có:
$AO=CO$ (gt)
\widehat{AOD} = \widehat{COB} (đối đỉnh)
$OD=OB$ (gt)
Vậy \bigtriangleup OAD = \bigtriangleup OCB (c.g.c)
Giải bài 4.13 trang 73 SGK Toán 7 tập 1 - Kết nối tri thức
a) Hãy tìm hai cặp tam giác có chung đỉnh $O$ bằng nhau;
b) Chứng minh rằng \bigtriangleup DAB = \bigtriangleup BCD
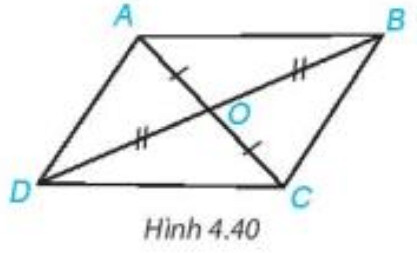
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
a, Xét \bigtriangleup AOB và \bigtriangleup COD có:
$AO = CO$ (gt)
\widehat{AOB} = \widehat{COD} (đối đỉnh)
$OB = OD$ (gt)
\Longrightarrow \bigtriangleup AOB= \bigtriangleup COD (c.g.c)
Xét \bigtriangleup AOD và \bigtriangleup COB có:
$AO = CO$ (gt)
\widehat{AOD} = \widehat{COB} (đối đỉnh)
$OD = OB$ (gt)
\Longrightarrow \bigtriangleup AOD= \bigtriangleup COB (c.g.c)
Vậy hai cặp tam giác có chung đỉnh $O$ bằng nhau là: AOB và COD; AOD và COB theo trường hợp cạnh – góc – cạnh.
b, Do \bigtriangleup AOD= \bigtriangleup COB nên: \widehat{ADO} = \widehat{CBO} (2 góc tương ứng) và $AD=BC$ (2 cạnh tương ứng)
Xét \bigtriangleup DAB và \bigtriangleup BCD có:
$AD=BC$ (cmt)
\widehat{ADO} = \widehat{CBO} (cmt)
$BD$ chung
Vậy \bigtriangleup DAB= \bigtriangleup BCD(c.g.c)
Giải bài 4.14 trang 73 SGK Toán 7 tập 1 - Kết nối tri thức
Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau.
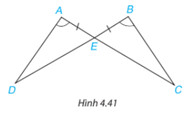
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Xét hai tam giác ADE và BCE có:
\widehat{A} = \widehat{B}
$AE=BE$
\widehat{AED} = \widehat{BEC} (đối đỉnh)
Vậy \bigtriangleup ADE= \bigtriangleup BCE(c.g.c)
Giải bài 4.15 trang 73 SGK Toán 7 tập 1 - Kết nối tri thức
a, \bigtriangleup ABE= \bigtriangleup DCE
b, $EG=EH$
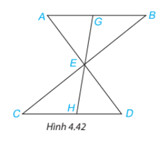
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
a)Xét hai tam giác ABE và DCE có:
\widehat{BAE} = \widehat{CDE} (so le trong )
$AB=CD$(gt)
\widehat{ABE} = \widehat{DCE} (so le trong )
Vậy \bigtriangleup ABE= \bigtriangleup DCE(g.c.g)
b)Xét hai tam giác BEG và CEH có:
\widehat{CEH} = \widehat{BEG} (đối đỉnh)
$CE=BE$ (do \bigtriangleup ABE= \bigtriangleup DCE)
\widehat{ECH} = \widehat{EBG} (so le trong)
\Longrightarrow \bigtriangleup BEG= \bigtriangleup CEH(g.c.g)
Vậy $EG=EH$ (hai cạnh tương ứng).
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Hy vọng, qua bài viết này bạn có thể nắm rõ tất cả các kiến thức có trong bài 14 chương 4 – Trường hợp bằng nhau thứ hai và thứ ba của tam giác trang 70, 71, 72, 73, 74 Toán 7 Kết Nối Tri Thức. Chúc các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





