Giải SGK Bài 2 Chương 7 trang 67, 68, 69, 70, 71, 72 Toán 10 Cánh diều tập 2

a) Cho $\vec{u}=(-2 ; 0), \vec{v}=(0 ; 6), \vec{w}=(-2 ; 3)$. Tìm tọa độ vectơ $\vec{u}+\vec{v}+\vec{w}$
b) Cho $\vec{u}=(\sqrt{3} ; 0), \vec{v}=(0 ; \sqrt{7})$. Tìm tọa độ của vectơ $\vec{w}$ sao cho $\vec{w}+\vec{u}=\vec{v}$

Lời giải chi tiết:
a) Tọa độ của vectơ $\vec{u}+\vec{v}+\vec{w}$ là: $\vec{u}+\vec{v}+\vec{w}=(-2+0+(-2) ; 0+6+3)=(-4 ; 9)$
b) Ta có: $\vec{w}+\vec{u}=\vec{v} \Leftrightarrow \vec{w}=\vec{v}-\vec{u}$ nên $\vec{w}=(0-\sqrt{3} ;-\sqrt{7}-0)=(-\sqrt{3} ;-\sqrt{7})$

Trong bài toán mở đầu, hãy tìm tọa độ của máy bay trực thăng tại thời điểm sau khi xuất phát 2 giờ.

Lời giải chi tiết:
Sau khi xuất phát được 2 giờ tức là máy bay đi được $\frac{2}{3}$ quãng đường thì ta có máy bay ở điểm $\mathrm{M}$ hay là ta có $\overrightarrow{A M}=\frac{2}{3} \overrightarrow{A B}$
Tọa độ vectơ $\overrightarrow{A B}=(-300 ; 400) \Rightarrow \overrightarrow{A M}=\left(-200 ; \frac{800}{3}\right)$
$\Rightarrow \overrightarrow{O M}=\overrightarrow{A M}-\overrightarrow{A O}=\left(-600 ; \frac{650}{3}\right)$
Vậy tọa độ máy bay sau 2 giờ xuất phát là: $\left(-600 ; \frac{650}{3}\right)$

Lời giải chi tiết:
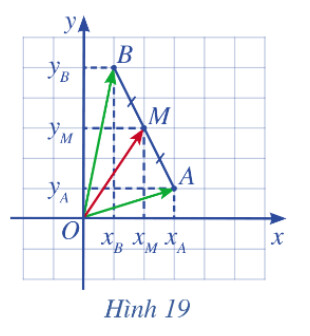
a) Ta có vectơ $\overrightarrow{O M}$ biểu diễn theo hai vectơ $\overrightarrow{O A}$ và $\overrightarrow{O B}$ là: $\overrightarrow{O M}=\frac{1}{2}(\overrightarrow{O A}+\overrightarrow{O B})$
b) Do tọa độ hai điểm A và B là: $A\left(x_A, y_A\right), B\left(x_B, y_B\right)$
nên ta có: $\overrightarrow{O A}=\left(x_A, y_A\right), \overrightarrow{O B}=\left(x_B, y_B\right)$
Vậy $\overrightarrow{O M}=\frac{1}{2}(\overrightarrow{O A}+\overrightarrow{O B})=\frac{1}{2}\left(x_A+x_B ; y_A+y_B\right)=\left(\frac{x_A+x_B}{2} ; \frac{y_A+y_B}{2}\right)$
Tọa độ điểm $\mathrm{M}$ chính là tọa độ của vectơ nên tọa độ $\mathrm{M}$ là $M\left(\frac{x_A+x_B}{2} ; \frac{y_A+y_B}{2}\right)$

Lời giải chi tiết:
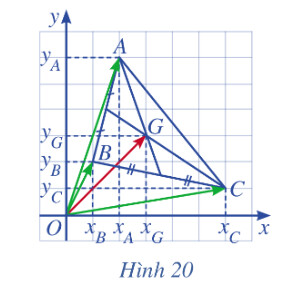
a) Ta có vectơ $\overrightarrow{O G}$ theo ba vectơ $\overrightarrow{O A}, \overrightarrow{O B}$ và $\overrightarrow{O C}$ là: $\overrightarrow{O G}=\frac{1}{3}(\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C})$
b) Do tọa độ ba điểm $\mathrm{A}, \mathrm{B}$ và $\mathrm{C}$ là: $A\left(x_A, y_A\right), B\left(x_B, y_B\right), C\left(x_C, y_C\right)$
Nên ta có: $\overrightarrow{O A}=\left(x_A, y_A\right), \overrightarrow{O B}=\left(x_B, y_B\right), \overrightarrow{O C}=\left(x_C, y_C\right)$
Vậy $\overrightarrow{O G}=\frac{1}{3}(\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C})=\frac{1}{3}\left(x_A+x_B+x_C ; y_A+y_B+y_C\right)=\left(\frac{x_A+x_B+x_C}{3} ; \frac{y_A+y_B+y_C}{3}\right)$
Tọa độ điểm G chính là tọa độ của vectơ $\overrightarrow{O G}$ nên tọa độ $\mathrm{G}$ là $G\left(\frac{x_A+x_B+x_C}{3} ; \frac{y_A+y_B+y_C}{3}\right)$

Cho hai điểm $A(2 ; 4)$ và $M(5 ; 7)$. Tìm toạ độ điểm $B$ sao cho $M$ là trung điểm đoạn thẳng $A B$.

Lời giải chi tiết:
Giả sử $\mathrm{B}$ có tọa độ: $B\left(x_B, y_B\right)$
Do $\mathrm{M}$ là trung điểm của đoạn thẳng $\mathrm{AB}$ nên:
\begin{cases}x_M=\frac{x_A+x_B}{2} \\ y_M=\frac{y_A+y_B}{2} \end{cases} \Leftrightarrow \begin{cases} x_B=2 x_M-x_A \\ y_B=2 y_M-y_A\end{cases} \Leftrightarrow \begin{cases} x_B=2.5-2=8 \\ y_B=2.7-4=10 \end{cases}
Vậy tọa độ điểm B là: $B(8 ; 10)$

Cho ba điểm $A(-1 ; 1)$, $B(1 ; 5), G(1 ; 2)$.
a) Chứng minh ba điểm $A$, $B, G$ không thẳng hàng.
b) Tìm toạ độ điểm $C$ sao cho $G$ là trọng tâm của tam giác $A B C$.

Lời giải chi tiết:
a) Ta có: $\overrightarrow{A B}=(2 ; 4), \overrightarrow{A G}=(2 ; 1)$
Do $\overrightarrow{A B} \neq k . \overrightarrow{A G}$ nên $\mathrm{A}, \mathrm{B}, \mathrm{G}$ không thẳng hàng
b) Giả sử C có tọa độ là: $C\left(x_C ; y_C\right)$
Để $\mathrm{G}$ là trọng tâm tam giác $\mathrm{ABC}$ thì: \\\\ \begin{cases} x_G=\frac{x_A+x_B+x_C}{3} \\ y_G=\frac{y_A+y_B+y_C}{3} \end{cases} \\\\ \\\\ \Longleftrightarrow \begin{cases} x_C=3 x_G-x_A-x_B \\ y_C=3 y_G-y_A-y_B \end{cases} \\\\ \Longleftrightarrow \begin{cases}x_C=3.1-(-1)-1=3 \\ y_C=3.2-1-5=0 \end{cases}
Vậy tọa độ điểm C là: $C(3 ; 0)$

Trong mặt phẳng tọa độ Oxy, cho $\vec{a}=(-1 ; 2), \vec{b}=(3 ; 1), \vec{c}=(2 ;-3)$.
a) Tìm tọa độ của vectơ $\vec{u}=2 \vec{a}+\vec{b}-3 \vec{c}$
b) Tìm tọa độ của vectơ $\vec{x}$ sao cho $\vec{x}+2 \vec{b}=\vec{a}+\vec{c}$

Lời giải chi tiết:
a) Tọa độ vectơ $\vec{u}=(2 .(-1)+3-3.2; 2.2+1-3 .(-3))=(-5 ; 14)$
b) Do $\vec{x}+2 \vec{b}=\vec{a}+\vec{c}$
$\Leftrightarrow \vec{x}=\vec{a}+\vec{c}-2 \vec{b}=(-1+2-2.3; 2+(-3)-2.1)=(-5 ;-3)$
Vậy $\vec{x}=(-5 ;-3)$

Trong mặt phẳng toạ độ $O x y$, cho $A(-2 ; 3), B(4 ; 5), C(2 ;-3)$.
a) Chứng minh ba điểm $A, B, C$ không thẳng hàng.
b) Tìm toạ độ trọng tâm $G$ của tam giác $A B C$.
c) Giải tam giác $A B C$.

Lời giải chi tiết:
a) Ta có: $\overrightarrow{A B}=(6 ; 2), \overrightarrow{A C}=(4 ;-6)$
Do $\overrightarrow{A B} \neq k . \overrightarrow{A C}$ nên $\mathrm{A}, \mathrm{B}, \mathrm{C}$ không thẳng hàng
b) Do $\mathrm{G}$ là trọng tâm tam giác $A B C$
Nên $\left\{\begin{array}{l}x_G=\frac{x_A+x_B+x_C}{3}=\frac{-2+4+2}{3}=\frac{4}{3} \\ y_G=\frac{y_A+y_B+y_C}{3}=\frac{3+5+(-3)}{3}=\frac{5}{3}\end{array}\right.$ Vậy $G\left(\frac{4}{3} ; \frac{5}{3}\right)$
c) Ta có:
$\overrightarrow{A B}=(6 ; 2), \overrightarrow{A C}=(4 ;-6), \overrightarrow{B C}=(-2 ;-8)$
$A B=|\overrightarrow{A B}|=\sqrt{6^2+2^2}=\sqrt{40}$
Suy ra:
$A C=|\overrightarrow{A C}|=\sqrt{4^2+(-6)^2}=\sqrt{52}$
$B C=|\overrightarrow{B C}|=\sqrt{(-2)^2+(-8)^2}=\sqrt{68}$
Ta có:
\cos \widehat{B A C}=\cos (\overrightarrow{A B}, \overrightarrow{A C})=\frac{6 \cdot 4+2 \cdot(-6)}{\sqrt{6^2+2^2} \cdot \sqrt{4^2+(-6)^2}} \approx 0,263 \Rightarrow \widehat{B A C} \approx 74^o \\ \cos \widehat{A B C}=\cos (\overrightarrow{B A}, \overrightarrow{B C})=\frac{(-6) \cdot(-2)+(-2) \cdot(-8)}{\sqrt{(-6)^2+(-2)^2} \cdot \sqrt{(-2)^2+(-8)^2}} \approx 0,47 \Rightarrow \widehat{A B C} \approx 62^o
Áp dụng tính chất tổng ba góc trong một tam giác ta có: $\widehat{A C B} \approx 180^{\circ}-74^{\circ}-62^{\circ} \approx 44^{\circ}$

Trong mặt phẳng toạ độ $O x y$, cho tam giác $A B C$ có trung điểm các cạnh $B C, C A, A B$ tương ứng là $M(2 ; 0), N(4 ; 2), P(1 ; 3)$.
a) Tìm toạ độ các điểm $A, B, C$.
b) Trọng tâm hai tam giác $A B C$ và $M N P$ có trùng nhau không? Vì sao?

Lời giải chi tiết:
a) Do $M, N, P$ là trung điểm của các cạnh $B C, C A, A B$ nên:
$\begin{aligned}& \left\{\begin{array} { l } { \frac { x _ { B } + x _ { C } } { 2 } = x _ { M } } \\{ \frac { x _ { B } + x _ { A } } { 2 } = x _ { P } } \\{ \frac { x _ { A } + x _ { C } } { 2 } = x _ { N } }\end{array} \Leftrightarrow \left\{\begin{array} { l } { x _ { B } + x _ { C } = 4 } \\{ x _ { B } + x _ { A } = 2 } \\{ x _ { A } + x _ { C } = 8 }\end{array} \Leftrightarrow \left\{\begin{array}{l}x_A=3 \\x_B=-1 \\x_C=5\end{array}\right.\right.\right. \\& \left\{\begin{array} { l } { \frac { y _ { B } + y _ { C } } { 2 } = y _ { M } } \\{ \frac { y _ { B } + y _ { A } } { 2 } = y _ { P } } \\{ \frac { y _ { A } + y _ { C } } { 2 } = y _ { N } }\end{array} \Leftrightarrow \left\{\begin{array} { l } { y _ { B } + y _ { C } = 0 } \\{ y _ { B } + y _ { A } = 4 } \\{ y _ { A } + y _ { C } = 6 }\end{array} \Leftrightarrow \left\{\begin{array}{l}y_A=5 \\y_B=-1 \\y_C=1\end{array}\right.\right.\right.\end{aligned}$
Vậy $A(3 ; 5), B(-1 ;-1), C(5 ; 1)$
b) Trọng tâm tam giác $A B C$ có tọa độ là: $\left\{\begin{array}{l}\frac{x_A+x_B+x_C}{3}=\frac{3+(-1)+5}{3}=\frac{7}{3} \\ \frac{y_A+y_B+y_C}{3}=\frac{5+(-1)+1}{3}=\frac{5}{3}\end{array}\right.$
Trọng tâm tam giác MNP có tọa độ là: $\left\{\begin{array}{l}\frac{x_M+x_N+x_P}{3}=\frac{2+4+1}{3}=\frac{7}{3} \\ \frac{y_M+y_N+y_P}{3}=\frac{0+2+3}{3}=\frac{5}{3}\end{array}\right.$
Vậy trọng tâm của 2 tam giác $A B C$ và MNP là trùng nhau vì có cùng tọa độ.

Trong mặt phẳng toạ độ $O x y$, cho tam giác $A B C$ có $A(2 ; 4), B(-1 ; 1), C(-8 ; 2)$.
a) Tính $\widehat{A B C}$.
b) Tính chu vi của tam giác $A B C$.
c) Tìm toạ độ điểm $M$ trên đường thẳng $B C$ sao cho diện tích của tam giác $A B C$ bằng hai lần diện tích của tam giác $A B M$.

Lời giải chi tiết:
a) Ta có:
$\overrightarrow{B C}=(-7 ; 1), \overrightarrow{B A}=(3 ; 3)$
$\cos \widehat{A B C}=(\overrightarrow{B C}, \overrightarrow{B A})=\frac{(-7) \cdot 3+1.3}{\sqrt{(-7)^2+1^2} \cdot \sqrt{3^2+3^2}}=-\frac{3}{5} \Rightarrow \widehat{A B C} \approx 126^{\circ}$
b) Ta có:
$\overrightarrow{B C}=(-7 ; 1), \overrightarrow{B A}=(3 ; 3), \overrightarrow{A C}=(-10 ;-2)$
$A B=|\overrightarrow{B A}|=\sqrt{3^2+3^2}=3 \sqrt{2}$
Suy ra:
$A C=|\overrightarrow{A C}|=\sqrt{(-10)^2+(-2)^2}=\sqrt{104}$
$B C=|\overrightarrow{B C}|=\sqrt{(-7)^2+1^2}=\sqrt{50}$
Vậy chu vi tam giác $A B C$ là: $P_{A B C}=2 \sqrt{26}+8 \sqrt{2}$
c) Để diện tích của tam giác $\mathrm{ABC}$ bằng hai lần diện tích của tam giác ABM thì M phải là trung điểm BC.
Vậy tọa độ điểm M là: $\left\{\begin{array}{l}\frac{x_B+x_C}{2}=\frac{-9}{2} \\ \frac{y_B+y_C}{2}=\frac{3}{2}\end{array}\right.$. Vậy $M\left(\frac{-9}{2} ; \frac{3}{2}\right)$

Cho ba điểm $A(1 ; 1), B(4 ; 3)$ và $C(6 ;-2)$.
a) Chứng minh ba điểm $A, B, C$ không thẳng hàng.
b) Tìm toạ độ điểm $D$ sao cho tứ giác $A B C D$ là hình thang có $A B / / C D$ và $C D=2 A B$.

Lời giải chi tiết:
a) Ta có: $\overrightarrow{A B}=(3 ; 2), \overrightarrow{A C}=(-1 ;-3)$
Do $\overrightarrow{A B} \neq k .\overrightarrow{A C}$ nên $\mathrm{A}, \mathrm{B}, \mathrm{C}$ không thẳng hàng
b) Giả sử tọa độ điểm $\mathrm{D}$ là: $D\left(x_D, y_D\right)$
Ta có: $\overrightarrow{C D}=\left(x_D-0 ; y_D-(-2)\right)=\left(x_D ; y_D+2\right)$
Để tứ giác $\mathrm{ABCD}$ là hình thang có $\mathrm{AB} / / \mathrm{CD}$ và $\mathrm{CD}=2 \mathrm{AB}$ thì $\overrightarrow{C D}=2 \overrightarrow{A B}$
Vậy nên $\overrightarrow{C D}=2 \overrightarrow{A B} \Leftrightarrow\left\{\begin{array}{l}x_D=2.3 \\ y_D+2=2.2\end{array} \Leftrightarrow\left\{\begin{array}{l}x_D=6 \\ y_D=2\end{array}\right.\right.$
Vậy tọa độ D là: $D(6 ; 2)$

Chứng minh khẳng định sau:
Hai vectơ $\vec{u}=\left(x_{1} ; y_{1}\right), \vec{v}=\left(x_{2} ; y_{2}\right)(\vec{v} \neq \overrightarrow{0})$ cùng phương khi và chỉ khi có một số thực $k$ sao cho $x_{1}=k x_{2}$ và $y_{1}=k y_{2}$.

Lời giải chi tiết:
Để hai vectơ $\vec{u}=\left(x_1, y_1\right), \vec{v}=\left(x_2, y_2\right)(\vec{v} \neq 0)$ cùng phương thì phải tồn tại một số $k$
$(k \in \mathbb{R})$ sao cho $\vec{u}=k . \vec{v} \Leftrightarrow\left\{\begin{array}{l}x_1=k x_2 \\ y_1=k y_2\end{array}\right.$ (ĐPCM)

Lời giải chi tiết:

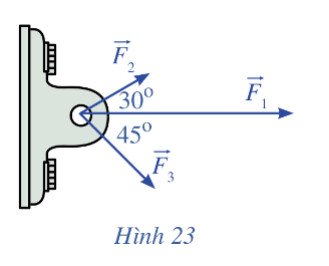
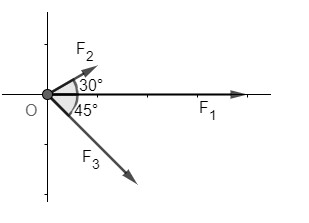
Chọn hệ trục tọa độ Oxy như hình vẽ
Ta có: $\overrightarrow{F_1}=(1500 ; 0)$
Do $\left(\overrightarrow{F_1}, \overrightarrow{F_2}\right)=30^{\circ}$ nên tọa độ của $\overrightarrow{F_2}$ là:
$\overrightarrow{F_2}=\left(600 . \cos 30^{\circ} ; 600 . \sin 30^{\circ}\right)=(300 \sqrt{3} ; 300)$
Do $\left(\overrightarrow{F_1}, \overrightarrow{F_3}\right)=45^{\circ}$ nên tọa độ của $\overrightarrow{F_3}$ là:
$\overrightarrow{F_3}=\left(800 . \cos 45^{\circ} ;-800 . \sin 45^{\circ}\right)=(400 \sqrt{2} ;-400 \sqrt{2})$
Do đó, lực $\vec{F}$ tổng hợp các lực tác động lên vật có tọa độ là:
$\vec{F}=\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=(1500+300 \sqrt{3}+400 \sqrt{2} ; 300-400 \sqrt{2})$
Độ lớn lực tổng hợp $\vec{F}$ tác động lên vật là:
$|\vec{F}|=\sqrt{(1500+300 \sqrt{3}+400 \sqrt{2})^2+(300-400 \sqrt{2})^2} \approx 2599(N)$