Giải SGK bài 2 trang 10,11,12,13 Toán 7 Kết nối tri thức tập 1
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Cộng trừ nhân chia số hữu tỉ. Đây là bài học thuộc bài 2 chương 1 ở các trang 10,11,12,13 SGK Toán 7 Kết nối tri thức tập 1. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi SGK trang 10,11,12,13 Toán 7 Kết nối tri thức
Các hoạt động khám phá, thực hành, vận dụng luyện tập ở các trang 10,11,12,13 này sẽ giúp các bạn đi vào bài học tìm hiểu các kiến thức về Cộng trừ nhân chia số hữu tỉ một cách trơn tru và dễ hiểu hơn rất nhiều đấy! Cùng xem lời giải của HocThatGioi nhé!
Câu hỏi mở đầu trang 10
+ Tính độ cao cao nhất khinh khí cầu đạt được
+ Tính khoảng cách khinh khí cầu di chuyển sau 27 giây giảm độ cao
+ Tính độ cao so với mặt đất
Độ cao cao nhất khinh khí cầu đạt được là: $0,8 \cdot 50=40$ $(\mathrm{m})$
Khoảng cách khinh khí cầu di chuyển sau 27 giây hạ độ cao là: $\frac{5}{9} \cdot 27=15(\mathrm{~m})$
Vậy sau 27 giây từ khi hạ độ cao, khinh khí cầu cách mặt đất: $40-15=25(\mathrm{~m})$
Hoạt động 1 trang 10
a) $\frac{-7}{8}+\frac{5}{12}$
b) $\frac{-5}{7}-\frac{8}{21}$
Quy tắc cộng, trừ phân số
Áp dụng quy tắc để tính
+) Quy tắc cộng 2 phân số:
Quy tắc cộng hai phân số cùng mẫu
Muốn cộng hai phân số có cùng mẫu số, ta cộng tử số với nhau và giữ nguyên mẫu số.
Quy tắc cộng hai phân số khác mẫu
Muốn cộng hai phân số khác mẫu, ta quy đồng mẫu số của chúng, sau đó cộng hai phân số có cùng mẫu.
+) Quy tắc trừ 2 phân số:
* Quy tắc cộng hai phân số cùng mẫu
Muốn trừ 2 phân số có cùng mẫu số, ta trừ tử của số bị trừ cho tử của số trừ và giữ nguyên mẫu.
* Quy tắc cộng hai phân số khác mẫu
Muốn trừ 2 phân số khác mẫu, ta quy đồng mẫu 2 phân số rồi trừ 2 phân số đó
a) $\frac{-7}{8}+\frac{5}{12} $
$=\frac{-21}{24}+\frac{10}{24} $
$=\frac{-11}{24}$
b) $\frac{-5}{7}-\frac{8}{21} $
$=\frac{-15}{21}-\frac{8}{21} $
$ =\frac{-23}{21}$
Hoạt động 2 trang 10
a) $0,25+1 \frac{5}{12}$
b) $-1,4-\frac{3}{5}$
Viết các hỗn số và số thập phân dưới dạng phân số
Muốn cộng hai phân số khác mẫu, ta quy đồng mẫu số của chúng, sau đó cộng hai phân số có cùng mẫu
Muốn trừ 2 phân số khác mẫu, ta quy đồng mẫu 2 phân số rồi trừ 2 phân số đó
a)$ 0,25+1 \frac{5}{12}=\frac{25}{100}+\frac{17}{12} $
$ =\frac{1}{4}+\frac{17}{12}=\frac{3}{12}+\frac{17}{12} $
$ =\frac{20}{12}=\frac{5}{3} $
$ b) -1,4-\frac{3}{5}$
$ =\frac{-14}{10}-\frac{3}{5}=\frac{-7}{5}-\frac{3}{5} $
$ =\frac{-10}{5}=-2$
Luyện tập 1 trang 11
a) $(-7)-\left(-\frac{5}{8}\right)$
b) $-21,25+13,3$
Áp dụng: $a-(-b)=a+b$ Cộng 2 số hữu tỉ trái dấu
$ a)(-7)-\left(-\frac{5}{8}\right) $
$ =(-7)+\frac{5}{8} $
$ =\frac{-56}{8}+\frac{5}{8} $
$ =\frac{-51}{8} $
$b)-21,25+13,3 $
$ =-(21,25-13,3) $
$ =-7,95$
Luyện tập 2 trang 11
a) $\frac{9}{10}-\left(\frac{6}{5}-\frac{7}{4}\right)$
b) $6,5+[0,75-(8,25-1,75)]$
Khi bỏ dấu ngoặc:
+) Nếu trước dấu ngoặc là dấu (+) thì ta bỏ dấu ngoặc và giữ nguyên dấu của các số hạng trong ngoặc.
+) Nếu trước dấu ngoặc là dấu (-) thì ta bỏ dấu ngoặc và đổi dấu của các số hạng trong ngoặc.
$a) \frac{9}{10}-\left(\frac{6}{5}-\frac{7}{4}\right) $
$ =\frac{9}{10}-\frac{6}{5}+\frac{7}{4} $
$ =\frac{18}{20}-\frac{24}{20}+\frac{35}{20} $
$ =\frac{18-24+35}{20} $
$ =\frac{29}{20}$
$ b) 6,5+[0,75-(8,25-1,75)] $
$ =6,5+(0,75-8,25+1,75) $
$ =6,5+0,75-8,25+1,75 $
$ =7,25-8,25+1,75 $
$ =(-1)+1,75 $
$ =0,75$
Vận dụng 1 trang 12
(Theo Viện Dinh dưỡng Quốc gia)
Em hãy cho biết khối lượng các chất còn lại trong $100g$
khoai tây khô.
Thực hiện phép trừ số hữu tỉ
Tổng khối lượng các chất trong 100 g khoai tây khô là 100 g.
Khối lượng các chất còn lại trong 100 g khoai tây khô là:
$100 – 11 – 6,6 – 0,3 – 75,1 = 7 (g)$
Hoạt động 3 trang 12
a) $0,36 \cdot \frac{-5}{9}$
b) $\frac{-7}{6}: 1 \frac{5}{7}$
Bước 1: Viết các hỗn số và số thập phân dưới dạng phân số
Bước 2: Thực hiện phép nhân, chia phân số
Muốn nhân 2 phân số, ta nhân tử với tử, mẫu với mẫu.
Muốn chia 2 phân số, ta nhân phân số thứ nhất với phân số nghịch đảo của phân số thứ 2.
$a) 0,36 \cdot \frac{-5}{9} $
$ =\frac{36}{100} \cdot \frac{-5}{9} $
$ =\frac{9}{25} \cdot \frac{-5}{9} $
$ =\frac{-1}{5}$
$b) \frac{-7}{6}: 1 \frac{5}{7} $
$ =\frac{-7}{6}: \frac{12}{7} $
$ =\frac{-7}{6} \cdot \frac{7}{12}$
$ =\frac{49}{72}$
Luyện tập 3 trang 12
a) $\left(-\frac{9}{13}\right) \cdot\left(-\frac{4}{5}\right)$
b) $-0,7: \frac{3}{2}$.
+) Viết số thập phân dưới dạng phân số
+) Thực hiện phép nhân, chia phân số
Muốn nhân 2 phân số, ta nhân tử với tử, mẫu với mẫu.
Muốn chia 2 phân số, ta nhân phân số thứ nhất với phân số nghịch đảo của phân số thứ 2.
$= (-\frac{9}{13}) \cdot (-\frac{4}{5})$
$= \frac{9}{13} \cdot \frac{4}{5} $
$= \frac{36}{65} $
$ b)-0,7: \frac{3}{2} $
$= \frac{-7}{10} \cdot \frac{2}{3} $
$= \frac{-7}{15}$
Tích của 2 số hữu tỉ trái dấu là 1 số hữu tỉ âm.
Luyện tập 4 trang 12
Viết số thập phân, hỗn số dưới dạng phân số
Sử dụng tính chất phân phối giữa phép nhân và phép cộng $(a.b+a.c = a.(b+c)$
$ \frac{7}{6} \cdot 3 \frac{1}{4}+\frac{7}{6} \cdot(-0,25) $
$ =\frac{7}{6} \cdot \frac{13}{4}+\frac{7}{6} \cdot \frac{-25}{100} $
$ =\frac{7}{6} \cdot \frac{13}{4}+\frac{7}{6} \cdot \frac{-1}{4} $
$ =\frac{7}{6} \cdot\left[\left(\frac{13}{4}+\left(-\frac{1}{4}\right)\right)\right] $
$ =\frac{7}{6} \cdot \frac{12}{4} $
$ =\frac{7}{6} \cdot 3$
$ =\frac{7}{2}$
Vận dụng 2 trang 13
Tính diện tích từng tấm ảnh và diện tích tờ giấy
Diện tích phần giấy ảnh còn lại = Diện tích tờ giấy – diện tích 2 tấm ảnh
Diện tích hình chữ nhật = Chiều dài . Chiều rộng
Diện tích 1 tấm ảnh là:
$10.15=150\left(\mathrm{~cm}^2\right)$
Diện tích tấm giấy là:
$21,6 \cdot 27,9=602,64\left(\mathrm{~cm}^2\right)$
Diện tích phần giấy ảnh còn lại là:
$602,64-2.150=302,64\left(\mathrm{~cm}^2\right)$
Đáp số: 302, 64 cm²
Giải bài tập SGK trang 13 Toán 7 Kết nối tri thức
Những bài tập SGK ở cuối bài Cộng trừ nhân chia số hữu tỉ trang 13 sách Toán 7 Kết nối tri thức sẽ giúp các bạn vận dụng những kiến thức vừa học để giải các bài tập từ cơ bản đến nâng cao. Cùng HocThatGioi giải quyết những bài toán này nhé!
Bài 1.7 trang 13
a) $\frac{-6}{18}+\frac{18}{27}$
b) $2,5-\left(-\frac{6}{9}\right)$
c) $-0,32 \cdot(-0,875)$;
d) $(-5): 2 \frac{1}{5}$
a)$ \frac{-6}{18}+\frac{18}{27} $
$ =\frac{-1}{3}+\frac{2}{3} $
$ =\frac{1}{3}$
$b) 2,5-\left(-\frac{6}{9}\right) $
$ =\frac{25}{10}+\frac{6}{9} $
$ =\frac{5}{2}+\frac{2}{3} $
$ =\frac{15}{6}+\frac{4}{6} $
$ =\frac{19}{6}$
$c) -0,32 \cdot(-0,875) $
$ =\frac{-32}{100} \cdot\left(-\frac{875}{1000}\right) $
$ =\frac{-8}{25} \cdot\left(\frac{-7}{8}\right) $
$ =\frac{8}{25} \cdot \frac{7}{8} $
$ =\frac{7}{25}$
$d)(-5): 2 \frac{1}{5} $
$ =(-5): \frac{11}{5} $
$ =(-5). \frac{5}{“} $
$ =\frac{-25}{11}$
Bài 1.8 trang 13
a) $\left(8+2 \frac{1}{3}-\frac{3}{5}\right)-(5+0,4)-\left(3 \frac{1}{3}-2\right)$;
b) $\left(7-\frac{1}{2}-\frac{3}{4}\right):\left(5-\frac{1}{4}-\frac{5}{8}\right)$.
+ Viết các số thập phân, hỗn số dưới dạng phân số.
+ Thực hiện phép cộng, trừ, chia phân số.
Chú ý:
Cách 1:Tính giá trị các biểu thức trong ngoặc trước
Cách 2: Phá ngoặc, nhóm các số hạng có cùng mẫu số
a) Cách 1:
$ \left(8+2 \frac{1}{3}-\frac{3}{5}\right)-(5+0,4)-\left(3 \frac{1}{3}-2\right)$
$ =\left(8+\frac{7}{3}-\frac{3}{5}\right)-\left(5+\frac{4}{10}\right)-\left(\frac{10}{3}-2\right) $
$ =8+\frac{7}{3}-\frac{3}{5}-5-\frac{2}{5}-\frac{10}{3}+2 $
$ =(8-5+2)+\left(\frac{7}{3}-\frac{10}{3}\right)-\left(\frac{3}{5}+\frac{2}{5}\right)$
$ =5+\frac{-3}{3}-\frac{5}{5} $
$ =5+(-1)-1 $
$ =3$
Cách 2:
$\left(8+2 \frac{1}{3}-\frac{3}{5}\right)-(5+0,4)-\left(3 \frac{1}{3}-2\right) $
$ =\left(8+\frac{7}{3}-\frac{3}{5}\right)-\left(5+\frac{4}{10}\right)-\left(\frac{10}{3}-2\right) $
$ =\left(\frac{120}{15}+\frac{35}{15}-\frac{9}{15}\right)-\left(\frac{25}{5}+\frac{2}{5}\right)-\left(\frac{10}{3}-\frac{6}{3}\right) $
$ =\frac{146}{15}-\frac{27}{5}-\frac{4}{3} $
$ =\frac{146}{15}-\frac{81}{15}-\frac{20}{15} $
$ =\frac{45}{15} $
$ =3$
b)
$ \left(7-\frac{1}{2}-\frac{3}{4}\right):\left(5-\frac{1}{4}-\frac{5}{8}\right) $
$ =\left(\frac{28}{4}-\frac{2}{4}-\frac{3}{4}\right):\left(\frac{40}{8}-\frac{2}{8}-\frac{5}{8}\right) $
$ =\frac{23}{4}: \frac{33}{8} $
$ =\frac{23}{4} \cdot \frac{8}{33} $
$ =\frac{46}{33}$
Bài 1.9 trang 13

Từ các số $-2; 10; 4; – 25$ , sử dụng phép cộng, trừ, nhân, chia, các dấu ngoặc ở được 1 phép tính có kết quả bằng $-105$
Cách 1: $(-2) \cdot 10 \cdot 4+(-25)$
Cách 2: $(-25)+4 \cdot(-2) \cdot 10$
Cách 3: $(-25) \cdot 4+10:(-2)$
Cách 4: $10:(-2)+4 \cdot(-25)$
Chú ý: Ta có thể đổi chỗ các thừa số trong tích (-2).10.4 hay các số hạng trong tổng (-2) . 10.4 +(-25)
Bài 1.10 trang 13
$0,65 \cdot 78+2 \frac{1}{5} \cdot 2020+0,35 \cdot 78-2,2 \cdot 2020$
+ Viết hỗn số về dạng số thập phân.
+ Nhóm các số hạng một cách hợp lí
+ Sử dụng tính chất và phân phối của phép nhân với phép cộng
$ 0,65.78+2 \frac{1}{5} .2020+0,35.78-2,2.2020 $
$ =0,65.78+2,2.2020+0,35.78-2,2.2020 $
$ =(0,65.78+0,35.78)+(2,2.2020-2,2.2020) $
$ =78 .(0,65+0,35)+0 $
$ =78.1 $
$ =78$
Bài 1.11 trang 13
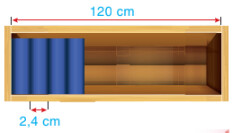
Thực hiện phép chia chiều dài ngăn sách cho chiều dày 1 cuốn sách.
Ngăn sách đó có thế để được nhiều nhất số cuốn sách như vậy là:
$120: 2,4=50$ (cuốn)
Đáp số: 50 cuốn
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 2 – Cộng trừ nhân chia số hữu tỉ trang 10,11,12,13 Toán 7 Kết nối tri thức tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





