Giải SGK bài 23 Quy tắc đếm trang 60, 61, 62, 63, 64, 65 Toán 10 Kết nối tri thức Tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Quy tắc đếm. Đây là bài học thuộc bài 23 chương VIII trang 60, 61, 62, 63, 64, 65 sách Toán 10 Kết nối tri thức tập 2. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi trong SGK của bài 23
Dưới đây là phương pháp và bài giải chi tiết cho câu hỏi mở đầu, câu hỏi hoạt động, vận dụng cùng phần luyện tập ở các trang 60, 61, 62, 63, 64, 65 trong bài Quy tắc đếm. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Câu hỏi mở đầu trang 60
Mỗi mật khẩu của một trang web là một dãy có từ 2 tới 3 kí tự, trong đó kí tự đầu tiên là một trong 26 chữ cái in thường trong bảng chữ cái tiếng Anh (từ a đến z), mỗi kí tự còn lại là một chữ số từ 0 đến 9 . Hỏi có thể tạo được bao nhiêu mật khẩu khác nhau?
Sau khi học bài này, ta sẽ giải quyết được bài toán mở đầu như sau:
Ta thấy có hai trường hợp: độ dài của mật khẩu là 2 hoặc 3 kí tự.
Trường hợp 1: độ dài mật khẩu là 2 kí tự. Chọn từng kí tự và áp dụng quy tắc nhân.
Kí tự đầu tiên có 26 cách chọn trong các chữ cái in thường tiếng Anh.
Kí tự thứ hai có 10 cách chọn trong các chữ số từ 0 đến 9.
Vậy theo quy tắc nhân, ta có:
$26.10=260$ cách chọn mật khẩu trong trường hợp 1 .
Trường hợp 2: độ dài mật khẩu là 3 kí tự.
Tương tự như trường hợp 1, ta có:
$26.10^2=2600$ cách chọn mật khẩu.
Vì có hai trường hợp rời nhau, mật khẩu có thể rơi vào một trong hai trường hợp, nên ta áp dụng quy tắc cộng.
Tổng số mật khẩu có thể là: $260+2600=2860$.
Hoạt động 1 trang 61
Từ Hà Nội vào Vinh mỗi ngày có 7 chuyến tàu hoả và 2 chuyến máy bay. Bạn An muốn ngày Chủ nhật này đi từ Hà Nội vào Vinh bằng tàu hoả hoặc máy bay.
Hỏi bạn An có bao nhiêu cách chọn chuyến đi?
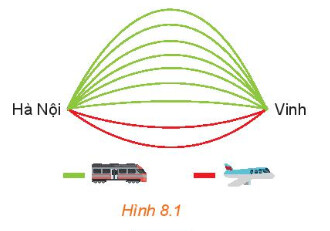
Để đi bằng tàu hỏa bạn An có 7 cách chọn và đi bằng máy bay có 2 cách chọn.
Vậy bạn An có tất cả $7+2=9$ cách chọn chuyến đi
Hoạt động 2 trang 61
a) Có bao nhiêu loại vé ghế ngồi và bao nhiêu loại vé giường nằm?
b) Có bao nhiêu loại vé để bạn An lựa chọn?
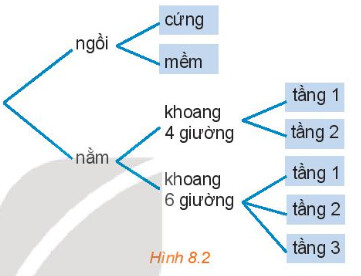
a) Số vé ghế ngồi là 2 (loại vé)
Số vé giường nằm là $2+3=5$ (loại vé)
b) Số loại vé để bạn An lựa chọn là:
$2+5=7$ (loại vé)
Luyện tập 1 trang 62
– Không nguyên tố cùng nhau = có ước chung (khác 1).
– Mà $35=5.7$ nên ta tìm các số chia hết cho 5 hoặc 7 .
Từ 1 đến 30 có:
– Có 6 số chia hết cho 5 là: $5,10,15,20,25,30$.
– Có 4 số chia hết cho 7 là: $7,14,21,28$.
Có tất cả $6+4=10$ số tự nhiên không nguyên tố cùng nhau với $35$ .
Hoạt động 3 trang 62
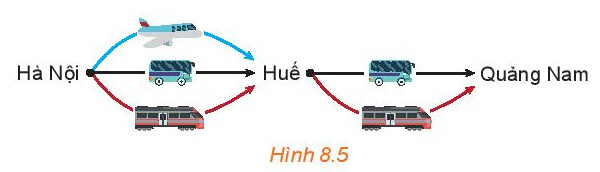
Hỏi thầy Trung có bao nhiêu cách chọn phương tiện để đi từ Hà Nội vào Quảng Nam?
Đi từ Hà Nội vào Huế, rồi từ Huế vào Quảng Nam có các cách là:
Máy bay $>>$ Ôtô
Máy bay $>>$ tàu hỏa
Ôtô $>>$ Ôtô
Ôtô $>>$ tàu hỏa
Tàu hỏa $>>$ Ôtô
Tàu hỏa $>>$ tàu hỏa
Vậy thầy Trung có 6 cách chọn phương tiện để đi từ Hà Nội vào Quảng Nam.
Hoạt động 4 trang 63
Hỏi có thể gắn nhãn tối đa được cho bao nhiêu ghế?
– Để gắn nhãn cho các ghế ta chọn chọn 1 chữ cái in hoa và 1 số (từ 1 đến 20 ).
– Số cách chọn chữ cái in hoa: 26 cách (tương ứng với 26 chữ)
– Số cách chọn số: 20 cách
Vậy số ghế gắn nhãn tối đa là $26.20=520$ (ghế)
Luyện tập 2 trang 64
– Mỗi bảng 4 đội thi đấu vòng tròn, giả sử là các đội $A, B, C, D$
Các trận đấu là: $A-B$, $A-C$, $A-D$, $B-C$, $B-D$, $C-D$ $=>$ có tất cả 6 trận đấu
– Có 8 bảng khác nhau.
– Tổng cộng vòng bảng có số trận đấu là $6.8=48$ (trận đấu).
Luyện tập 3 trang 64
a) Là số tự nhiên có ba chữ số khác nhau?
b) Là số tự nhiên chẵn có ba chữ số khác nhau?
a) Từ 4 chữ số $0,1,2,3$ :
– Hàng trăm có 3 cách chọn.
– Hàng chục có 3 cách chọn.
– Hàng đơn vị có 2 cách chọn.
Vậy có tất cả $3.3.2=18$ số tự nhiên khác nhau có 3 chữ số được lập từ 0, 1, 2, 3 .
b)
– Trường hợp 1: hàng đơn vị là số 0 như vậy hàng trăm có 3 cách chọn, hàng chục có 2 cách chọn.
Có tất cả $1.2.3=6$ số có thể lập được.
– Trường hợp 2: hàng đơn vị là số 2 như vậy hàng trăm có 2 cách chọn, hàng chục có 2 cách chọn.
Có tất cả $1. 2. 2= 4$ số có thể lập được.
Vậy có thể lập $6+4=10$ số tự nhiên chẳn có ba chữ số khác nhau.
Vận dụng trang 65
Chia 3 trường hợp:
– 2 bạn lớp 10A, 1 bạn lớp 10B, 1 bạn lớp 10C.
– 1 bạn lớp 10A, 2 bạn lớp 10B, 1 bạn lớp 10C.
– 1 bạn lớp 10A, 1 bạn lớp 10B, 2 bạn lớp 10C.
Áp dụng quy tắc nhân tính từng trường hợp có bao nhiêu cách chọn và quy tắc cộng để cộng 3 trường hợp với nhau.
TH1: 2 bạn lớp 10A, 1 bạn lớp 10B, 1 bạn lớp 10C có số cách chọn là:
$30.29.35.32=974400$ (cách)
TH2: 1 bạn lớp 10A, 2 bạn lớp 10B, 1 bạn lớp 10C có số cách chọn là:
$30. 35. 34. 32= 1142400$ (cách)
TH3: 1 bạn lớp 10A, 1 bạn lớp 10B, 2 bạn lớp 10C có số cách là:
$30. 35. 32. 31=1041600$ (cách)
Vậy số cách lựa chọn là: $974400+1142400+1041600=3158400$ cách
Giải bài tập vận dụng trang 65 SGK Toán 10 bài 23
Phần tiếp theo sẽ cung cấp cho các bạn phương pháp cùng lời giải trong phần bài tập trang 65 cực kỳ dễ hiểu và chi tiết. Cùng HocThatGioi rèn luyện và nâng cao kỹ năng giải quyết các vấn đề thực tế thông qua các phương pháp, công thức toán học từ bài Quy tắc đếm ở trên.
Bài tập 8.1 trang 65
Áp dụng quy tắc cộng.
Theo bài ra, ta vẽ được sơ đồ hình cây như sau:
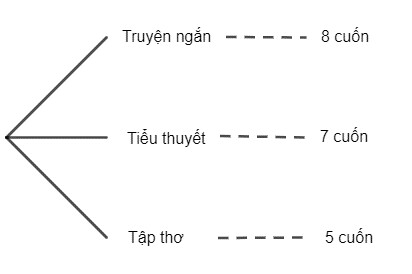
Số cách chọn một cuốn để đọc là: $8 + 7 + 5 = 20$ (cách).
Vậy bạn Phong có $20$ cách chọn một cuốn để đọc vào ngày cuối tuần.
Bài tập 8.2 trang 65
Áp dụng quy tắc nhân.
Mỗi lần gieo có 2 khả năng xảy ra: xấp hoặc ngửa
Nếu người đó gieo 3 lần thì có thể có số khả năng xảy ra là:
2.2.2 = 8 (khả năng)
Bài tập 8.3 trang 65
a) Sự tổ hợp giữa hai gen tạo ra mấy kiểu gen? Viết các kiểu gen đó.
b) Khi giao phối ngẫu nhiên, có bao nhiêu kiểu giao phối khác nhau từ các kiểu gen đó?
a) Sự tổ hợp giữa hai gen tạo ra 3 kiểu gen: $AA, aa, Aa$.
b) Khi giao phối ngẫu nhiên, có số kiểu giao phối khác nhau từ các kiểu gen đó là: $3.3= 9$ ( kiểu)
Bài tập 8.4 trang 65
a) có 3 chữ số khác nhau?
b) là số lẻ có 3 chữ số khác nhau?
c) là số có 3 chữ số và chia hết cho 5 ?
d) là số có 3 chữ số khác nhau và chia hết cho 5 ?
Áp dụng kết hợp quy tắc cộng và quy tắc nhân.
Chọn các chữ số hàng trăm, hàng chục, hàng đơn vị trong các chữ số $0,1,2,3,4,5,6,7,8,9$.
a)
– Chữ số hàng trăm có 9 cách (khác 0)
– Chữ số hàng chục có 9 cách (khác chữ số hàng trăm)
– Chữ số hàng đơn vị có 8 cách (khác chữ số hàng trăm và hàng chục)
Vậy có tất cả $9. 9. 8= 648$ số tự nhiên có 3 chữ số khác nhau.
b)
– Chọn chữ số hàng đơn vị có 5 cách
– Chọn chữ số hàng trăm có 8 cách
– Chọn chữ số hàng chục có 8 cách
Vậy có tất cả $5. 8. 8= 320$ số lẻ có 3 chữ số khác nhau.
c)
– Chọn chữ số hàng đơn vị có 2 cách
– Chọn chữ số hàng trăm có 9 cách
– Chọn chữ số hàng chục có 10 cách
Vậy có tất cả $2.9.10=180$ số tự nhiên có 3 chữ số chia hết cho 5 .
d)
Trường hợp 1: chữ số hàng đơn vị là 0 .
– Chọn chữ số hàng trăm có 9 cách
– Chọn chữ số hàng chục có 8 cách
Trường hợp 2: chữ số hàng đơn vị là 5 :
– Chọn chữ số hàng trăm có 8 cách (khác 0 và 5)
– Chọn chữ số hàng chục có 8 cách
Vậy có tất cả $9.8+8.8=136$ số tự nhiên có 3 chữ số khác nhau và chia hết cho 5 .
Bài tập 8.5 trang 65
b) Nếu chương trình máy tính quy định mới mật khẩu vẫn gồm 3 kí tự, nhưng kí tự đầu tiên phải là một chữ cái in hoa trong bảng chữ cái tiếng Anh gồm 26 chữ (từ $A$ đến $Z$ ) và 2 kí tự sau là các chữ số (từ 0 đến 9 ). Hỏi quy định mới có thể tạo được nhiều hơn quy định cũ bao nhiêu mật khẩu khác nhau?
a) Mỗi kí tự đều có 10 cách chọn.
Số mật khẩu có thế tạo ra là $10.10 .10=1000$
b)
– Kí tự đầu có 26 cách chọn.
– 2 kí tự sau, mỗi kí tự có 10 cách chọn.
Quy định mới có thể tạo ra số mật khẩu là:
$26.10 .10=2600$
Quy định mới có thể tạo được nhiều hơn quy định cũ số mật khẩu khác nhau là:
$$2600-1000=1600 \text { (mật khẩu) }$$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Quy tắc đếm Chương Đại số tổng hợp Toán 10 Kết nối tri thức tập 2 ở các trang 60, 61, 62, 63, 64, 65. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!





