Giải SGK bài 26 trang 31, 32, 33 Toán 7 Kết nối tri thức Tập 2
Bài học Phép cộng và phép trừ đa thức một biến, là một bài học hay, bổ ích. Thuộc Chương 7 bài 26, trang 31, 32, 33 SGK Toán 7 Kết nối tri thức Tập 2. Dưới đây là những phương pháp giải rất đơn giản, dễ hiểu và chi tiết của HocThatGioi. Cho những hoạt động, luyện tập, vận dụng cũng như bài tập sách giáo khoa ở các trang 32, 33 mà các bạn sẽ được học trong bài này. Cùng theo dõi ngay nhé!
Giải SGK mục 1 trang 31, 32 Toán 7 Kết nối tri thức Tập 2
Hãy cùng HocThatGioi đi tìm đáp án nhanh nhất, chính xác nhất cho mục 1 trang 31, 32. Của bài Phép cộng và phép trừ đa thức một biển nhé.
Giải SGK câu hỏi 1 trang 32
Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Cách 1:
$(x^{3} – 5x + 2) + (x^{3}– x^{2}+6x – 4)$
$= x^{3}– 5x + 2 + x^{3}– x^{2}+6x – 4$
$=(x^{3}+ x^{3}) – x^{2} + (– 5x + 6x) + (2 – 4)$
$= 2x^{3} – x^{2}+ x – 2$
Giải SGK luyện tập 1 trang 32
Hãy tính tổng $M + N$ ( trình bày theo $2$ cách)
Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Cách 2: Đặt tính cộng sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng theo từng cột.
Cách 1:
$M + N = (0,5x^{4} – 4x^{3} + 2x – 2,5) + ( 2x^{3} + x^{2}+ 1,5)$
$= 0,5x^{4} – 4x^{3} + 2x – 2,5 + 2x^{3} + x^{2}+ 1,5$
$= 0,5x^{4} + (– 4 x^{3} + 2x^{3} ) + x^{2} + 2x + (-2,5 + 1,5)$
$= 0,5x^{4} + (– 2x^{3} ) + x^{2} + 2x + (-1)$
$= 0,5x^{4} – 2x^{3} + x^{2} + 2x – 1$
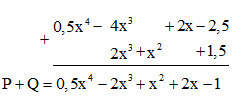
Giải SGK vận dụng 1 trang 32
$A = 2x^{3} – 5x^{2} + x – 7$
$B = x^{2} – 2x + 6$
$C = -x^{3}+ 4x^{2} – 1$
Đặt tính cộng sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng theo từng cột.
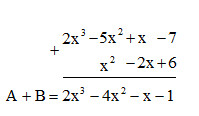
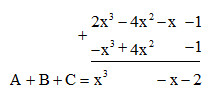
Vậy $A + B + C = x^{3}- x – 2$.
Giải SGK mục 2 trang 32, 33 Toán 7 Kết nối tri thức tập 2
Sau khi tìm hiểu xong mục 1-Cộng hai đa thức một biến. Thì bây giờ chúng ta đến với mục 2-Trừ hai đa thức một biến. Mục 2 là phần hữa hẹn sẽ có nhiều kiến thức thú vị và bổ ích. Hãy cùng đón xem nhé!
Giải SGK hoạt động 1 trang 32
Tìm hiệu $P – Q$ bằng cách bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.
+ Bước 1: Bỏ dấu ngoặc: Trước dấu ngoặc là dấu “ –“ thì ta bỏ dấu ngoặc đồng thời đổi dấu tất cả các số hạng trong ngoặc.
+Bước 2: Nhóm các hạng tử cùng bậc
+ Bước 3: Thu gọn
Ta có: $P – Q = x^{4} + 3x^{3} – 5x^{2} + 7x – (-x^{3} + 4x^{2} – 2x +1)$
$= x^{4} + 3x^{3} – 5x^{2} + 7x + x^{3} – 4x^{2} – 4x^{2} + 2x – 1$
$= x^{4} + (3x^{3}+ x^{3} ) + (– 5x^{2} – 4x^{2} ) + (7x + 2x ) – 1$
$= x^{4} + 4x^{3} – 9x^{2} + 9x – 1$
Giải SGK hoạt động 2 SGK trang 32
Tìm hiệu $P – Q$ bằng cách đặt tính trừ: đặt đa thức $Q$ dưới đa thức $P$ sao cho các hạng tử cùng bậc thẳng cột với nhau rồi trừ theo từng cột.
Bước 1: Đặt đa thức $Q$ dưới đa thức $P$ sao cho các hạng tử cùng bậc thẳng cột với nhau
Bước 2: Trừ theo từng cột
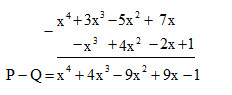
Giải SGK luyện tập 2 trang 32
$M = 0,5x^{4}– 4x^{3} + 2x – 2,5$ và $N = 2x^{3} + x^{2} + 1,5$
Hãy tính hiệu $M – N$ (trình bày theo $2$ cách)
Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Cách 2: Đặt tính trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi trừ theo từng cột.
Cách 1:
$M – N = (0,5x^{4} – 4x^{3} + 2x – 2,5) – ( 2x^{3} + x^{2} + 1,5)$
$= 0,5x^{4} – 4x^{3} + 2x – 2,5 – 2x^{3} – x^{2} – 1,5$
$= 0,5x^{4} + (– 4x^{3} – 2x^{3} ) – x^{2} + 2x + (-2,5 – 1,5)$
$= 0,5x^{4}+ (– 6x^{3} ) – x^{2} + 2x + (-4)$
$= 0,5x^{4} – 6x^{3} – x^{2}+ 2x – 4$
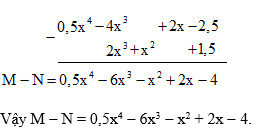
Vậy $M – N = 0,5x^{4} – 6x^{3} – x^{2} + 2x – 4$.
Giải SGK vận dụng 2 trang 33
$A + B = 2x^{5} + 5x^{3} – 2$
$A – C = x^{3}$
$B = (A + B) – A$
$C = A – (A – C)$
Thực hiện phép trừ đa thức:
Bỏ dấu ngoặc: Trước dấu ngoặc là dấu “ –“ thì ta bỏ dấu ngoặc đồng thời đổi dấu tất cả các số hạng trong ngoặc rồi nhóm các hạng tử cùng bậc.
Ta có:
$B = (A + B) – A = 2x^{5} + 5x^{3} – 2 – (x^{4} – 3x^{2} – 2x + 1)$
$= 2x^{5} + 5x^{3} – 2 – x^{4} + 3x^{2} + 2x – 1$
$= 2x^{5} – x^{4} + 5x^{3} + 3x^{2} + (-2 – 1)$
$= 2x^{5} – x^{4} + 5x^{3} + 3x^{2} – 3$
$C = A – (A – C) = x^{4} – 3x^{2} – 2x + 1 – x^{3}$
$= x^{4} – x^{3}– 3x^{2} – 2x + 1$
Vậy $B = 2x^{5} – x^{4} + 5x^{3} + 3x^{2} – 3$
$C = x^{4} – x^{3}– 3x^{2} – 2x + 1$
Giải SGK bài tập trang 33 Toán 7 Kết nối tri thức Tập 2
Đồng hành cùng HocThatGioi, áp dụng những kiến thức lý thuyết đã học. Cùng nhau giải nhanh các bài tập, của bài 26 – Phép cộng và phép trừ đa thức một biết trang 33 nhé.
Giải SGK bài 7.12 trang 33
$x^{2} – 3x + 2$ và $4x^{3} – x^{2} + x – 1$
Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Ta có: $(x^{2} – 3x + 2) + (4x^{3} – x^{2} + x – 1)$
$= x^{2} – 3x + 2 + 4x^{3} – x^{2} + x – 1$
$= 4x^{3} + (x^{2} – x^{2} ) + (-3x + x) + (2 – 1)$
$= 4x^{3} – 2x + 1$
Giải SGK bài 7.13 trang 33
Đặt tính trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi trừ theo từng cột.
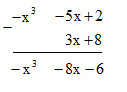
Giải SGK bài 7.14 trang 33
$A=6x^{4} – 4x^{3}+x-\frac{1}{3}$;
$B = -3x^{4} – 2x^{3}-5x^{2}+x+\frac{2}{3}$.
Tính $A + B$ và $A – B$
Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Cách 2: Đặt tính cộng (trừ) sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng (trừ ) theo từng cột.
$A+B$ = $(6x^{4} – 4x^{3}+x-\frac{1}{3})$ + ($-3x^{4} – 2x^{3}-5x^{2}+x+\frac{2}{3}$)
= $6x^{4} – 4x^{3}+x-\frac{1}{3}$ – $3x^{4} – 2x^{3}-5x^{2}+x+\frac{2}{3}$
$=(6x^{4}-3x^{4})+(-4x^{3}-2x^{3})- 5x^{2} +(x+x) + (-\frac{1}{3}+\frac{2}{3})$
$= 3x^{4}-6x^{3}-5x^{2}+2x+\frac{1}{3}$
$A-B$ = ($6x^{4} – 4x^{3}+x-\frac{1}{3}$) – ($-3x^{4}-2x^{3}-5x^{2}+x+\frac{2}{3}$)
= $6x^{4} – 4x^{3}+x-\frac{1}{3}$ + $3x^{4} + 2x^{3}+5x^{2}- x- \frac{2}{3}$
= $(6x^{4}+3x^{4})+(-4x^{3}+ 2x^{3})- 5x^{2} +(x-x) + (-\frac{1}{3}-\frac{2}{3})$
= $9x^{4}+(-2x^{3})+5x^{2}+(-1)$
= $9x^{4}-2x^{3}+5x^{2}-1$
Vậy $A+B$=$ 3x^{4}-6x^{3}-5x^{2}+2x+\frac{1}{3}$; $A-B$=$9x^{4}-2x^{3}+5x^{2}-1$
Giải SGK bài 7.15 trang 33
Tính $A + B + C$; $A – B + C$ và $A – B – C$.
Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
$A + B + C = (3x^{4} – 2x^{3} – x + 1) + (-2x^{3} + 4x^{2} + 5x) + (-3x^{4} + 2x^{2} + 5)$
$A + B + C = 3x^{4} – 2x^{3} – x + 1 + (-2x^{3}) + 4x^{2} + 5x + (-3x^{4}) + 2x^{2} + 5$
$A + B + C = (3x^{4} – 3x^{4}) + (-2x^{3} – 2x^{3}) + (4x^{2} + 2x^{2}) + (-x + 5x) + (1 + 5)$
$A + B + C = -4x^{3} + 6x^{2} + 4x + 6.$
$A – B + C = (3x^{4} – 2x^{3} – x + 1) – (-2x^{3} + 4x^{2} + 5x) + (-3x^{4} + 2x^{2} + 5)$
$A – B + C = 3x^{4} – 2x^{3} – x + 1 + 2x^{3} – 4x^{2} – 5x – 3x^{4} + 2x^{2} + 5$
$A – B + C = (3x^{4} – 3x^{4}) + (-2x^{3} + 2x^{3}) + (-4x^{2} + 2x^{2}) + (-x – 5x) + (1 + 5)$
$A – B + C = -2x^{2} + (-6x) + 6$
$A – B + C = -2x^{2} – 6x + 6.$
$A – B – C = (3x^{4} – 2x^{3} – x + 1) – (-2x^{3} + 4x^{2} + 5x) – (-3x^{4} + 2x^{2} + 5)$
$A – B – C = 3x^{4} – 2x^{3} – x + 1 + 2x^{3} – 4x^{2} – 5x + 3x^{4} – 2x^{2} – 5$
$A – B – C = (3x^{4} + 3x^{4}) + (-2x^{3} + 2x^{3}) + (-4x^{2} – 2x^{2}) + (-x – 5x) + (1 – 5)$
$A – B – C = 6x^{4} + (-6x^{2}) + (-6x) + (-4)$
$A – B – C = 6x^{4} – 6x^{2} – 6x – 4.$
Vậy $A + B + C = -4x^{3} + 6x^{2} + 4x + 6$; $A – B + C = -2x^{2} – 6x + 6$;
$A – B – C = 6x^{4} – 6x^{2} – 6x – 4.$
Giải SGK bài 7.16 trang 33
a) Viết các đa thức biểu thị số tiền Nam phải trả cho từng loại sách.
b) Tìm đa thức biểu thị tổng số tiền Nam phải trả để mua số sách đó.
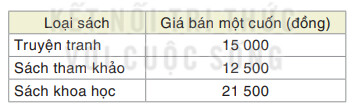
Viết đa thức biểu thị số tiền
Tiền mua $1$ loại sách = số cuốn . giá tiền một cuốn
a) Đa thức biểu thị số tiền Nam phải trả cho truyện tranh là: $A = (x +5). 15 000 = 15 000x + 75 000$ (đồng)
Đa thức biểu thị số tiền Nam phải trả cho sách tham khảo là: $B = (x + 8) . 12 500 = 12 500x + 100 000$ (đồng)
Đa thức biểu thị số tiền Nam phải trả cho sách khoa học là: $C = x . 21 500$ (đồng)
b) Đa thức biểu thị tổng số tiền Nam phải trả để mua số sách đó là:
$P = A + B + C = = 15 000x + 75 000 + 12 500x + 100 000 + x . 21 500$
$= (15 000 + 12 500 + 21 500)x + (75 000 + 100 000)$
$= 49 000x + 175 000$ ( đồng)
Giải SGK bài 7.17 trang 33
a) Biểu thị diện tích bể bơi
b) Biểu thị diện tích mảnh đất
c) Biểu thị diện tích phần đất xung quanh bể bơi.
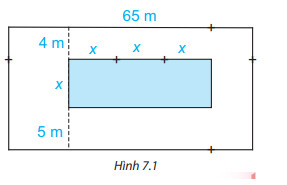
+ Biểu thị chiều dài và chiều rộng của các hình chữ nhật
Diện tích hình chữ nhật = chiều dài . chiều rộng
a) Do chiều dài của bể bơi gấp $3$ lần chiều rộng nên chiều dài của bể bơi là $3x$ $m$.
Diện tích của bể bơi là $3x.x = 3x^{2}$ ($m^{2}$).
b) Chiều rộng của mảnh đất là: $4 + x + 5 = x + 9$ ($m$).
Diện tích mảnh đất là: $65(x + 9)$ ($x^{2}$).
c) Diện tích phần đất xung quanh bể bơi bằng diện tích mảnh đất trừ đi diện tích bể bơi.
Diện tích phần đất xung quanh bể bơi bằng:
$65(x + 9) – 3x^{2}= 65x + 65.9 – 3x^{2} = – 3x^{2} + 65x + 585$ ($m^{2}$).
Vậy là bài học hôm nay đã khép lại rồi. Hy vọng các bạn hiểu va vận dụng hết tất cả các kiến thức có trong bài học ngày hôm nay. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 26 trang 31, 32, 33 Toán 7 Kết nối tri thức tập 2 nhé. Chúc các bạn học tốt nhé!!





