Giải SGK Bài 3 Chương 7 trang 15, 16, 17 Toán 10 Chân trời sáng tạo tập 2
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các hoạt động khởi động, vận dụng, bài tập trong bài Phương trình quy về phương trình bậc hai. Các bài tập sau đây thuộc Bài 3 Chương VII SGK Toán 10 Chân trời sáng tạo tập 2 ở các trang 15, 16, 17. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK Bài 3 Chương 7 Toán 10 Chân trời sáng tạo tập 2
Những lời giải dưới đây sẽ giúp bạn đi tìm đáp án cho các hoạt động khởi động, khám phá, thực hành và vận dụng ở các trang 15, 16, 17 trong sách Toán 10 Chân trời sáng tạo một cách nhanh chóng và dễ hiểu. Cùng theo dõi ngay nhé!
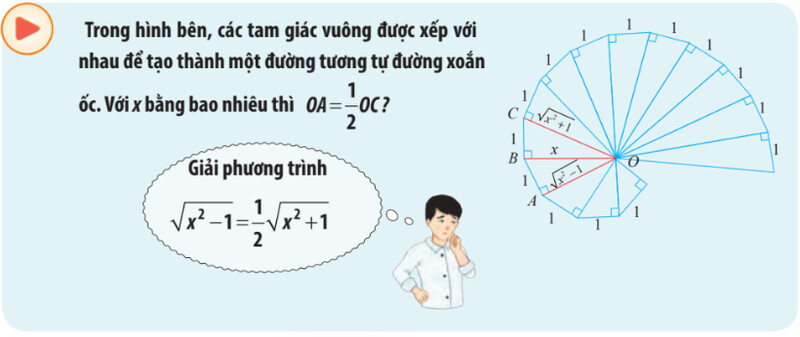
Hoạt động khởi động
Bước 1: Bình phương hai vế làm mất căn bậc hai
Bước 2: Rút gọn và giải phương trình vừa tìm được
Bước 3: Thử lại nghiệm vừa tìm được và kết luận
Ta có điều kiện hiểu nhiên $x>0$
$\sqrt{x^2-1}=\frac{1}{2} \sqrt{x^2+1}$
$\Rightarrow x^2-1=\frac{1}{4}\left(x^2+1\right)$
$\Rightarrow \frac{3}{4} x^2-\frac{5}{4}=0$
$\Rightarrow x= \pm \sqrt{\frac{5}{3}}$
Thử lại, kết hợp điều kiện của $x$ ta thấy $x=\sqrt{\frac{5}{3}}$ thỏa mãn phương trình.
Vậy khi $x=\sqrt{\frac{5}{3}}$ thì $O A=\frac{1}{2} O C$
Hoạt động khám phá 1 trang 15
$\sqrt{-2 x^2-2 x+11}=\sqrt{-x^2+3}$
$\Rightarrow-2 x^2-2 x+11=-x^2+3$ (bình phương cả hai vế để làm mất dấu căn)
$\Rightarrow x^2+2 x-8=0$ (chuyển vế, rút gọn)
$\Rightarrow x=2$ hoặc $x=-4$ (giải phương trình bậc hai)
Vậy phương trình đã cho có hai nghiệm là 2 và -4
Thay $x=2$ vào phương trình $\sqrt{-2 x^2-2 x+11}=\sqrt{-x^2+3}$ ta thấy không thỏa mãn vì dưới dấu căn là -1 không thỏa mãn
Vậy $x=2$ không là nghiệm của phương trình do đó lời giải như trên là sai.
Hoạt động khám phá 2 trang 16
$\sqrt{-x^2+x+1}=x$
$\Rightarrow-x^2+x+1=x^2$ (bình phương cả hai vế để làm mất dấu căn)
$\Rightarrow-2 x^2+x+1=0 \quad$ (chuyển vế, rút gọn)
$\Rightarrow x=1$ hoặc $x=-\frac{1}{2}$ (giải phương trình bậc hai)
Vậy phướng trình đã cho có hai nghiệm là 1 và $-\frac{1}{2}$
Thay nghiệm tìm được vào phương trình ban đầu ta có:
+) Thay $x=1$ vào phương trình $\sqrt{-x^2+x+1}=x$ ta thấy thảo mãn phương trình
+) Thay $x=-\frac{1}{2}$ vào $\sqrt{-x^2+x+1}=x$ ta thấy không thỏa mãn phương trình
Vậy nghiệm của phương trình là $x=1$, suy ra lời giải như trên là sai.
Thực hành 1 trang 16
Bước 1: Bình phương hai vế của phương trình để làm mất dấu căn
Bước 2: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn
Bước 3: Giải phương trình nhận được ở bước 2
Bước 4: Thử lại xem nghiệm đã tìm được ở bước 3 có thỏa mãn phương trình không và kết luận
Bình phương hai vế của phương trình đã cho, ta được:
$\sqrt{31 x^2-58 x+1}=\sqrt{10 x^2-11 x-19}$
$\Rightarrow 31 x^2-58 x+1=10 x^2-11 x-19$
$\Rightarrow 21 x^2-47 x+20=0$
$\Rightarrow x=\frac{5}{3}$ hoặc $x=\frac{4}{7}$
Thay lần lượt các nghiệm trên vào phương trình đã cho, ta thấy không có nghiệm nào thỏa mãn
Vậy phương trình đã cho vô nghiệm
Chú ý khi giải: sau khi bình phương hai vế thì các bước giải tiếp theo chỉ được sử dụng dấu suy ra không được sử dụng dấu tương đương (vì tập nghiệm của chúng có thể không giống nhau)
Thực hành 2 trang 16
Bước 1: Bình phương hai vế của phương trình để làm mất dấu căn
Bước 2: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn
Bước 3: Giải phương trình nhận được ở bước 2
Bước 4: Thử lại và kết luận
Bình phương hai vế của phương trình đã cho, ta được:
$3 x^2+27 x-41=(2 x+3)^2$
$\Rightarrow 3 x^2+27 x-41=4 x^2+12 x+9$
$\Rightarrow x^2-15 x+50=0$
$\Rightarrow x=5$ và $x=10$
Thay hai nghiệm vừa tìm được vào phương trình $\sqrt{3 x^2+27 x-41}=2 x+3$ ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy nghiệm của phương trình đã cho là $x=5$ và $x=10$
Vận dụng trang 17
a) $O C=3 O A$
b) $O C=\frac{5}{4} O B$
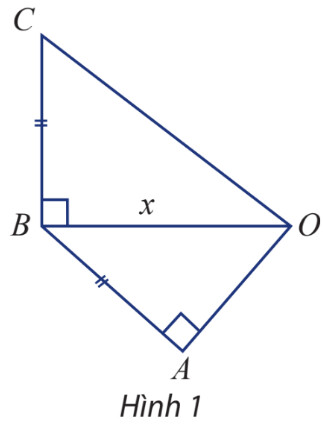
Bước 1: Sử dụng giả thiết và áp dụng định lý pitago để biểu diễn độ dài $OC$ và $OA$ qua $OB$
Bước 2: Lập phương trình theo giả thiết $O C=3 O A ; O C=\frac{5}{4} O B$
Bước 3: Giải phương trình
Gọi độ dài cạnh $O B$ là $x \mathrm{~cm}(x>0)$
Theo giả thiết ta có $A B=B C=O B-1=x-1$
Áp dụng định lý pitago trong tam giác vuông $O A B$ và $O B C$ ta có:
$O C=\sqrt{O B^2+B C^2}=\sqrt{x^2+(x-1)^2}=\sqrt{2 x^2-2 x+1}$
$O A=\sqrt{O B^2-A B^2}=\sqrt{x^2-(x-1)^2}=\sqrt{2 x-1}$
a) $O C=3 O A \Rightarrow \sqrt{2 x^2-2 x+1}=3 \sqrt{2 x-1}$
$\Rightarrow 2 x^2-2 x+1=9(2 x-1)$
$\Rightarrow 2 x^2-20 x+10=0$
$\Rightarrow x=5-2 \sqrt{5}$ và $x=5+2 \sqrt{5}$
Thay hai nghiệm vừa tìm được vào phương trình $\sqrt{2 x^2-2 x+1}=3 \sqrt{2 x-1}$ ta thấy cả hai đều thỏa mãn phương trình Vậy khi $O B=5-2 \sqrt{5}$ hoặc $O B=5+2 \sqrt{5}$ thì $O C=3 O A$
b) $O C=\frac{5}{4} O B \Rightarrow \sqrt{2 x^2-2 x+1}=\frac{5}{4} x$
$\Rightarrow 2 x^2-2 x+1=\frac{25}{16} x^2$
$\Rightarrow \frac{7}{16} x^2-2 x+1=0$
$\Rightarrow x=\frac{4}{7}$ hoặc $x=4$
Thay hai nghiệm vừa tìm được vào phương trình $\sqrt{2 x^2-2 x+1}=\frac{5}{4} x$ ta thấy cả hai nghiệm đều thỏa mãn phương trình Vậy khi $O B=\frac{4}{7}$ hoặc $O B=4(\mathrm{~cm})$ thì $O C=\frac{5}{4} O B$
Giải bài tập SGK Bài 3 Phương trình quy về phương trình bậc hai Toán 10 Chân trời sáng tạo
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Phương trình quy về phương trình bậc hai trang 17 sách Toán 10 Chân trời sáng tạo dưới đây nhé!
Bài tập 1 trang 17
a) $\sqrt{11 x^{2}-14 x-12}=\sqrt{3 x^{2}+4 x-7}$
b) $\sqrt{x^{2}+x-42}=\sqrt{2 x-30}$
c) $2 \sqrt{x^{2}-x-1}=\sqrt{x^{2}+2 x+5}$
d) $3 \sqrt{x^{2}+x-1}-\sqrt{7 x^{2}+2 x-5}=0$
Bước 1: Bình phương hai vế của phương trình để làm mất dấu căn
Bước 2: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn
Bước 3: Giải phương trình nhận được ở bước 2
Bước 4: Thử lại nghiệm và kết luận
a) $\sqrt{11 x^2-14 x-12}=\sqrt{3 x^2+4 x-7}$
$\Rightarrow 11 x^2-14 x-12=3 x^2+4 x-7$
$\Rightarrow 8 x^2-18 x-5=0$
$\Rightarrow x=-\frac{1}{4}$ và $x=\frac{5}{2}$
Thay nghiệm vừa tìm được vào phương trình $\sqrt{11 x^2-14 x-12}=\sqrt{3 x^2+4 x-7}$ ta thấy chỉ có nghiệm $x=\frac{5}{2}$ thảo mãn phương trình.
Vậy nghiệm của phương trình đã cho là $x=\frac{5}{2}$
b)$\sqrt{x^2+x-42}=\sqrt{2 x-30} $
$ \Rightarrow x^2+x-42=2 x-3 $
$ \Rightarrow x^2-x-12=0 $
$ \Rightarrow x=-3$ và $x=4$
Thay vào phương trình $\sqrt{x^2+x-42}=\sqrt{2 x-30}$ ta thấy không có nghiệm nào thỏa mãn
Vậy phương trình đã cho vô nghiệm
c) $2 \sqrt{x^2-x-1}=\sqrt{x^2+2 x+5} $
$ \Rightarrow 4 .\left(x^2-x-1\right)=x^2+2 x+5$
$ \Rightarrow 3 x^2-6 x-9=0 $
$ \Rightarrow x=-1 $ và $x=3$
Thay hai nghiệm trên vào phương trình $2 \sqrt{x^2-x-1}=\sqrt{x^2+2 x+5}$ ta thấy cả hai nghiệm đều thỏa mãn phương trình.
Vậy nghiệm của phương trình $2 \sqrt{x^2-x-1}=\sqrt{x^2+2 x+5}$ là $x=-1$ và $x=3$
d) $ 3 \sqrt{x^2+x-1}-\sqrt{7 x^2+2 x-5}=0$
$ \Rightarrow 3 \sqrt{x^2+x-1}=\sqrt{7 x^2+2 x-5}$
$ \Rightarrow 9 \cdot\left(x^2+x-1\right)=7 x^2+2 x-5 $
$ \Rightarrow 2 x^2+7 x-4=0 $
$ \Rightarrow x=-4 \text { và } x=\frac{1}{2}$
Thay hai nghiệm trên vào phương trình $3 \sqrt{x^2+x-1}-\sqrt{7 x^2+2 x-5}=0$ ta thấy chỉ có nghiệm $x=-4$ thỏa mãn phương trình
Vậy nghiệm của phương trình trên là $x=-4$
Bài tập 2 trang 17
a) $\sqrt{x^{2}+3 x+1}=3$;
b) $\sqrt{x^{2}-x-4}=x+2$;
c) $2+\sqrt{12-2 x}=x$
d) $\sqrt{2 x^{2}-3 x-10}=-5$.
Bước 1: Chuyển biểu thức có căn về một vế
Bước 2: Bình phương hai vế của phương trình để làm mất dấu căn
Bước 3: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn
Bước 4: Giải phương trình nhận được ở bước 2
Bước 5: Thử lại nghiệm và kết luận
a) $\sqrt{x^2+3 x+1}=3 $
$ \Rightarrow x^2+3 x+1=9 $
$ \Rightarrow x^2+3 x-8=0 $
$ \Rightarrow x=\frac{-3-\sqrt{41}}{2} \text { và } x=\frac{-3+\sqrt{41}}{2}$
Thay hai nghiệm trên vào phương trình $\sqrt{x^2+3 x+1}=3$ ta thấy cả hai nghiệm đều thỏa mãn phương trình.
Vậy nghiệm của phương trình đã cho là $x=\frac{-3-\sqrt{41}}{2}$ và $x=\frac{-3+\sqrt{41}}{2}$
b) $\sqrt{x^2-x-4}=x+2$
$ \Rightarrow x^2-x-4=(x+2)^2 $
$ \Rightarrow x^2-x-4=x^2+4 x+4 $
$ \Rightarrow 5 x=-8 $
$ \Rightarrow x=-\frac{8}{5} $
Thay $x=-\frac{8}{5}$ và phương trình $\sqrt{x^2-x-4}=x+2$ ta thấy thỏa mãn phương trình
Vậy nghiệm của phương trình đã cho là $x=-\frac{8}{5}$
c) $ 2+\sqrt{12-2 x}=x$
$ \Rightarrow \sqrt{12-2 x}=x-2 $
$ \Rightarrow 12-2 x=(x-2)^2 $
$ \Rightarrow 12-2 x=x^2-4 x+4 $
$ \Rightarrow x^2-2 x-8=0$
$ \Rightarrow x=-2 \text { và } x=4$
Thay hai nghiệm vừa tìm được vào phương trình $2+\sqrt{12-2 x}=x$ thì thấy chỉ có $x=4$ thỏa mãn.
Vậy $x=4$ là nghiệm của phương trình đã cho.
d) Ta có biểu thức căn bậc hai luôn không âm nên $\sqrt{2 x^2-3 x-10} \geq 0 \forall x \in \mathbb{R}$
$\Rightarrow \sqrt{2 x^2-3 x-10}=-5$(vô lí)
Vậy phương trình đã cho vô nghiệm
Bài tập 3 trang 17
a) Biểu diễn độ dài cạnh huyền $B C$ theo $A B$
b) Biết chu vi của tam giác $A B C$ là $24 \mathrm{~cm}$. Tìm độ dài ba cạnh của tam giác đó.
a) Bước 1: Đặt độ dài cạnh $AB$ là $x$ ($x \gt 0$), biểu diễn $AC$ theo $AB$
Bước 2: Áp dụng định lý Pitago biểu diễn cạnh $BC$
b) Bước 1: Lập biểu thức tính chu vi của tam giác
Bước 2: Giải phương trình vừa tìm được
a) Đặt độ dài cạnh $A B$ là $x(x>0)$
Theo giả thiết ta có độ dài $A C=A B+2=x+2$
Áp dụng định lý pitago trong tam giác vuông ta có
$B C=\sqrt{A B^2+A C^2}=\sqrt{x^2+(x+2)^2}=\sqrt{2 x^2+4 x+4}$
b) Chu vi của tam giác là $C=A B+A C+B C$
$\Rightarrow C=x+(x+2)+\sqrt{2 x^2+4 x+4}=2 x+2+\sqrt{2 x^2+4 x+4}$
Theo giả thiết ta có
$C=24 \Leftrightarrow 2 x+2+\sqrt{2 x^2+4 x+4}=24$
$\Leftrightarrow \sqrt{2 x^2+4 x+4}=22-2 x$
$\Rightarrow 2 x^2+4 x+4=(22-2 x)^2$
$\Rightarrow 2 x^2+4 x+4=4 x^2-88 x+484$
$\Rightarrow 2 x^2-92 x+480=0$
$\Rightarrow x=6$ hoặc $x=40$
Thay hai nghiệm vừa tìm được vào phương trình $\sqrt{2 x^2+4 x+4}=22-2 x$ ta thấy chỉ có $x=6$ thỏa mãn phương trình.
Vậy độ dài ba cạnh của tam giác là $A B=6 ; A C=8$ và $B C=10(\mathrm{~cm})$
Bài tập 4 trang 17
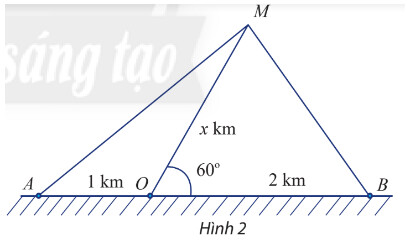
a) Đặt độ dài của $M O$ là $x \mathrm{~km}$. Biểu diễn khoảng cách từ tàu đến $A$ và từ tàu đến $B$ theo $x$.
b) Tìm $x$ để khoảng cách từ tàu đến $B$ bằng $\frac{4}{5}$ khoảng cách từ tàu đến $A$.
c) Tìm $x$ đễ khoảng cách từ tàu đến $B$ nhỏ hơn khoảng cách từ tàu đến $O$ đúng $500 \mathrm{~m}$.
Lưu ý: Làm tròn kết quả đến hàng phần trăm.
a) Sử dụng định lý $\operatorname{cosin} a^2=b^2+c^2+2 b c \cos A$
b) Lập phương trình $M B=\frac{4}{5} M A$, và giải phương trình lập được
c) Lập phương trình $M B=M O-0,5$, và giải phương trình lập được
a) Đặt độ dài của $M O$ là $x \mathrm{~km}(x>0)$
Ta có: $\widehat{M O A}+\widehat{M O B}=180^{\circ}$ (hai góc bù nhau) $\Rightarrow \widehat{M O A}=120^{\circ}$
Áp dụng định lý Cosin trong tam giác ta tính được:
+) Khoảng cách từ tàu đến $B$ là $M B=\sqrt{x^2+2^2-2 . 2 . x . \cos 60^{\circ}}=\sqrt{x^2-2 x+4}$
+) Khoảng cách từ tàu đến $A$ là $M A=\sqrt{x^2+1^2-2 . 1 . x . \cos 120^{\circ}}=\sqrt{x^2+x+1}$
b) Theo giải thiết ta có phương trình $M B=\frac{4}{5} M A \Rightarrow \sqrt{x^2-2 x+4}=\frac{4}{5} \sqrt{x^2+x+1}$
$\Rightarrow x^2-2 x+4=\frac{16}{25}\left(x^2+x+1\right)$
$\Rightarrow \frac{9}{25} x^2-\frac{66}{25} x+\frac{84}{25}=0$
$\Rightarrow x \simeq 1,64$ và $x \simeq 5,69$
Thay hai nghiệm vừa tìm được vào phương trình $\sqrt{x^2-2 x+4}=\frac{4}{5} \sqrt{x^2+x+1}$ ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy khi $x \simeq 1,64$ hoặc $x \simeq 5,69$ thì khoảng cách từ tàu đến $B$ bằng $\frac{4}{5}$ khoảng cách từ tàu đến $A$
c) Đổi $500 \mathrm{~m}=0,5 \mathrm{~km}$
Theo giả thiết ta có phương trình sau:
$M B=M O-0,5 \Rightarrow \sqrt{x^2-2 x+4}=x-0,5$
$\Rightarrow x^2-2 x+4=(x-0,5)^2$
$\Rightarrow x^2-2 x+4=x^2-x+\frac{1}{4}$
$\Rightarrow x=\frac{15}{4}$
Thay $x=\frac{15}{4}$ vào phương trình $\sqrt{x^2-2 x+4}=x-0,5$ ta thấy thỏa mãn phương trình
Vậy khi $x=\frac{15}{4}$ thì khoảng cách từ tàu đến $B$ nhỏ hơn khoảng cách từ tàu đến $O$ đúng $500 \mathrm{~m}$.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK Bài 3 Chương 7 Toán 10 Chân trời sáng tạo tập 2 ở các trang 15, 16, 17. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





